简单选择排序,树形选择排序,堆排序详解
选择类排序的基本思想:每一趟在n-i+1个记录中选取关键字最小的记录作为有序序列中第i个记录,本篇博客主要介绍简单选择排序,并在其基础上给出了改进算法——树形选择排序(也称作锦标赛排序),堆排序。
简单选择排序
【算法思想】
第一趟简单选择排序时,从第一个记录开始,通过n-1次关键字比较,从n个记录中选出关键字最小的记录,并和第一个记录交换。
第二趟简单选择排序时,从第二个记录开始,通过n-2次关键字比较,从n-1个记录中选出关键字最小的记录,并
和第二个记录交换。
。。。
第i趟简单选择排序时,从第n-i个记录开始,通过n-i次关键字比较,从n-i+1个记录中选出关键字最小的记录,并
和第i个记录交换。
如此反复,经过n-1趟简单选择排序,将把n-1个记录排到位,剩下一个最小记录直接在最后,所以共需n-1趟简单
选择排序。
void SelectSort(int arr[], int size)//选择排序
{
for (int i = 0; i < size; ++i)
{
for (int j = i + 1; j < size; ++j)
{
if (arr[j]在简单选择排序中,所需的移动记录的次数比较少。最好情况下,即待排序列初始状态就已经是正序排序了,不
需要移动记录。最坏情况下,即第一个记录最大,其余记录从小到大有序排列,此时移动次数最多,为3(n-1)次。
简单选择排序过程中需要进行比较的次数与初始状态下待排序的记录序列的排列无关。当i=1时,需进行n-1次,
当i=2时,需进行n-2次,以此类推,进行比较操作的时间复杂度为O(n^2)。
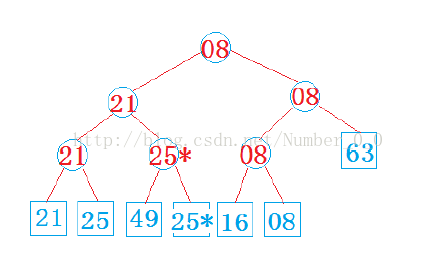
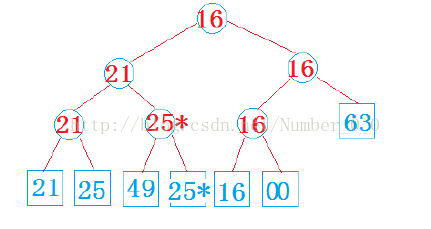
树形选择排序(锦标赛排序)
【算法思想】
首先取得n个元素的关键码,进行两两比较,得到n/2(上取整)个比较的优胜者(关键码小者),作为第一步比较
的结果保留下来。然后对这n/2(上取整)个元素再进行关键码的两两比较,…,如此重复,直到选出一个关键码最小
的元素为止。
一旦选择出这个元素,就需要在下次选择最小关键码之前把它的值该位最大值,使它再也不能战
胜其他对手,在此基础上需要重构胜者树所得到的最终胜者,是该排序下的下一个元素,重构的
时间代价为lg(N)。
总共需重构N-1次,锦标赛排序的时间复杂度为N*lgN
typedef struct rec
{
int data;
int index;
bool active; //节点未出局,则是true,其它false
}Rec;
void fixUpTree(Rec* tree, int pos) //从pos位置向上调整
{
int i = pos;
if (i % 2) //i位于右子树
tree[(i - 1) / 2] = tree[i + 1]; //左孩子上升到父节点
else
tree[(i - 1) / 2] = tree[i - 1]; //右孩子上升到父节点
i = (i - 1) / 2;
int j;
while (i) //上升到根节点,则终止循环
{
i % 2 ? j = i + 1 : j = i - 1; //确定i的兄弟j的下标
if (!tree[i].active || !tree[j].active) //左右孩子有一个为空
{
if (tree[i].active)
tree[(i - 1) / 2] = tree[i];
else
tree[(i - 1) / 2] = tree[j];
}
else //左右孩子都不为空
{
if (tree[i].data <= tree[j].data)
tree[(i - 1) / 2] = tree[i];
else
tree[(i - 1) / 2] = tree[j];
}
i = (i - 1) / 2; //回到上一层
}
}
void TreeSelectSort(int a[], int n) //树形选择排序
{
int i = 0;
while (pow(double(2), i) < n)
i++;
int leaf = pow(2, i); //完全二叉树叶子节点个数
int size = 2 * leaf - 1; //树节点总数 提示3
Rec *tree = new Rec[size]; //顺序存储一棵树
for (i = 0; i < leaf; i++)
{
if (i < n)
{
//leaf-1是叶子节点的起始下标,想想是这样吗?
tree[i + leaf - 1].data = a[i];
tree[i + leaf - 1].index = i;
tree[i + leaf - 1].active = true;
}
else//叶子节点下标从 leaf-1+n开始,后面都是空的,无此参赛者
tree[i + leaf - 1].active = false;
}
i = leaf - 1; //提示3
int j;
while (i) //上升到根节点,则终止循环
{
j = i;
while (j<2 * i) //下面的提示4
{
//无右节点或右节点已出局,即使存在右节点,其值域也比左节点大
if (!tree[j + 1].active || tree[j + 1].data>tree[j].data)
tree[(j - 1) / 2] = tree[j];
else
tree[(j - 1) / 2] = tree[j + 1];
j += 2; //两两比较
}
i = (i - 1) / 2; //回到上一层
}
i = 0;
while (i < n - 1) //确定剩下的n-1个节点的次序
{
a[i] = tree[0].data;
tree[leaf - 1 + tree[0].index].active = false; //出局,不参与下一轮
//每次出局后都需调整
fixUpTree(tree, leaf - 1 + tree[0].index);
i++;
}
a[n - 1] = tree[0].data; //最后一个归位
delete[]tree;
}堆排序
【算法思想】
利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性,使得每次从无序中选择最大记录(最小记录)变得
简单。其基本思想为(大顶堆):
1)将初始待排序关键字序列(R1,R2....Rn)构建成大顶堆,此堆为初始的无须区;
2)将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足
R[1,2...n-1]<=R[n];
3)由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆,然后再次
将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直
到有序区的元素个数为n-1,则整个排序过程完成。
操作过程如下:
1)初始化堆:将R[1..n]构造为堆;
2)将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换,然后将新的无序区调整为新的堆。
因此对于堆排序,最重要的两个操作就是构造初始堆和调整堆,其实构造初始堆事实上也是调整堆的过程,只不过
构造初始堆是对所有的非叶节点都进行调整。
void HeapAdjust(int arr[], int root, int size)
{
int parent = root;
int child = root * 2 + 1;
while (child < size)
{
if (child + 1= 0; --idx)
{
HeapAdjust(arr, idx, size);
}
int index = size - 1;
while (index > 0)
{
std::swap(arr[0], arr[index]);
HeapAdjust(arr, 0, index);
index--;
}
} 相关链接:插入类排序:点击打开链接
交换类排序:点击打开链接