蓝桥杯校内模拟赛

b内存

在计算机存储中，15.125GB是多少MB？

1字节(b)=8比特(bit)
1千字节(kb)=1024字节(b)
1兆字节(mb)=1024千字节(kb)
1千兆字节(gb)=1024兆字节(mb)

d树的叶子节点树

一棵包含有2019个结点的树，最多包含多少个叶结点？
下面这个图是我的理解，不知道对不对错的话希望大神指出。

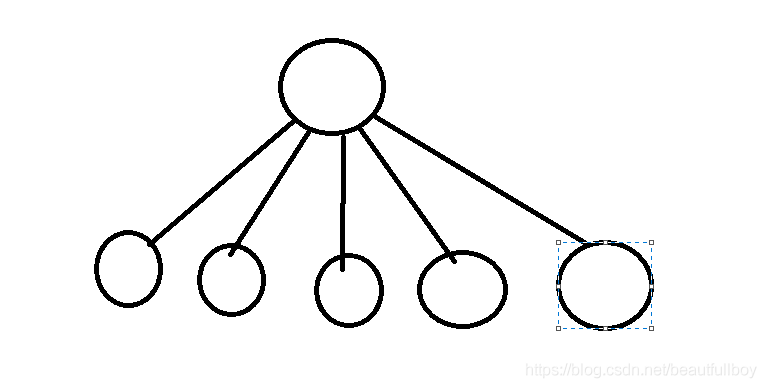
树和二叉树不同，不要和二叉树混了，树的一个节点下面可以分很多
节点，二叉树一个节点下面分两个。
一次n个结点的树最多可以包含n-1个叶节点。

下面是补充一个关于二叉树的一个题：

一棵结点数为2015的二叉树最多有多少个叶子结点'
答：二叉树有一个性质，即①叶子节点 = 度为2的节点数+1
所以二叉树叶子节点最多的时，即度为2的节点数也最多，这种情况出
现完全二叉树树种，2015个节点的完全二叉树。
②2015 = 叶子节点N0 + 度为1的节点N1+ 度为2的节点N2
连理①和②得当N1 = 0时，N0 = 1008 ，最多有1008个。 

E

这种题是个需要学习记住的思路，按我平常的思路肯定要复杂多了。

思路：
对输入的字符串从下表1判断s[i]是否等于s[i-1],不等于k++；该判断
通过ok()函数，如果是元音字母就返回1（true）否则返回0，将复杂
化为简单，用一个函数将字符串转换了0和1，1是元音字母，0是辅音
字母，这样只要第一个字符是0，并且有三个s[i]!=s[i-1]就满足条
件。重点是记住这个思维。

代码如下：

#include
#include
using namespace std;
string s;
bool ok(char a)
{
    if(a=='a'||a=='e'||a=='i'||a=='o'||a=='u')
        return 1;
        return 0;
}
int main()
{
    cin>>s;
    int k=0;
    int len=s.length();
    for(int i=1;i<len;i++)
    {
        if(ok(s[i])!=ok(s[i-1]))
            k++;
    }
if(!ok(s[0])&&k==3)
    cout<<"yes";
else
    cout<<"no";
    return 0;
}

F

首先解释一下这个题，我就是没有申请题，迷惑了，对于这红提以后一定要长记性，首相从一判断到n时间复杂度是1000000，而将一个n个位数转换到int数组中是6，因此6*1000000并不会超时，而我将转换到int数组时间复杂度也判断为了1000000，以后应该长记性。
代码如下：

#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int maxn=1e6+10;
char s[maxn];
bool ok(int k)
{
    vector<int> arrayInt;//这个注意定义在bool函数中，免去了每次清空arrayInt，我调试了一次//(ㄒoㄒ)/~~。
    while(k!=0){
        arrayInt.push_back(k%10);//我测试了，不能像数组一样下利用下标等于。
        k/=10;
    }
    reverse(arrayInt.begin(),arrayInt.end());//倒置vector注意咋写的，从begin()到end()；
   for(int i=1;i<(int)arrayInt.size();i++)//默认从1开始。//注意这里的size()要转换为int;//注意这里不能用length()，
   //以后统一用size()吧。
    if(arrayInt[i]<arrayInt[i-1])
    return 0;
   return 1;
}
int main()
{
    int n;
    cin>>n;
    ll ans=0;
    for(int i=1;i<=n;i++)
        if(ok(i))//也可以改成ans+=ok(i);
            ans++;
        cout<<ans;
        return 0;
}

G

这题方法很厉害，要努力学呀。
定义三个int数组，分别是输入的样例、前缀最小值、后缀最大值。学会这个利用前后缀。记住记住记住！！
这样的话在遍历数组的时候只要看他是否大于他前面的最小值，并且是否小于它后面的最大值，就行了。
代码如下：

#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int maxn=1e3+10;
int a[maxn],b[maxn],c[maxn];
ll ans=0;
int main()
{
    int n;
    cin>>n;
    ll ans=0;
    for(int i=1;i<=n;i++)cin>>a[i];
    b[1]=a[1];c[n]=a[n];
    for(int i=2;i<=n;i++)b[i]=(a[i]<b[i-1])?a[i]:b[i-1];
    for(int i=n-1;i>=1;i--)c[i]=(a[i]>c[i+1])?a[i]:c[i+1];
    for(int i=2;i<=n-1;i++)//注意这里是从2开始到n-1结束
    {
        if(a[i]>b[i-1]&&a[i]<c[i+1])//写的时候犯病了，在这加了个分号
        ans++;
    }
    cout<<ans;
    return 0;
}

H

题目描述：

递归两个两个的递归，在mian函数里面第一个都是n,第二个枚举，然后在递归函数里面再次枚举，第一个是第二个传参，第二个枚举。注意函数里面
总和定为1，因为每次只要传过来就满足条件，直接就是1，后来再加，注意这里为了减少时间复杂度，要用一个二阶数组记住每次传过来的i，j。
这一题还有让我知道了，竞赛另一个思路：有时候写的题准确但是超时，可以用打表，把答案定义在一个数组中。在根据输入的数输出对应的数组即
答案。

代码如下：

#include
#include
#include
using namespace std;
const int maxn=1e4+10;
int ans=0;
int rem[maxn][maxn];
const int  mod=1e4;
int dfs(int i,int j)
{
    if(rem[i][j]!=-1)return rem[i][j];
    //if(j==1) return 1;
    int sum=1;
    for(int k=1;k<abs(i-j);k++)
        sum=(sum+dfs(j,k))%mod;
        rem[i][j]=sum;
        return sum;
}
int main()
{
    memset(rem,-1,sizeof(rem));
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
      ans=(ans+dfs(n,i))%mod;
    cout<<ans;
}

I

这题如果用普通的暴力，会超时。
这里用了STL中的queue，这还是我第一次用queue。。
这题重点还是在代码中：

#include
#include
#include//queue的头文件。
using namespace std;
const int maxn=1e3+10;
char s[maxn][maxn];
int ps[4][2]={1,0,-1,0,0,1,0,-1};//这个顺序无所谓，但要每个都包括进去，并且不能重复。
struct Lawn{
int x,y,t;
}lawn;//这里用了结构体。很关键！
int main()
{
    int n,m,k;
    cin>>n>>m;
    queue<Lawn> q;//定义一个queue的结构体变量。
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            cin>>s[i][j];
            cin>>k;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
    {
        if(s[i][j]=='g')
            q.push((Lawn){i,j,k});//这个写法需要记住！
    }
    while(!q.empty())
    {
        Lawn pe=q.front();q的第一个量
        q.pop();弹出q的第一个元素，注意vector的pop_back()是删除最后一个元素。
        for(int i=0;i<4;i++)//注意在ps
        {
            int i1=pe.x+ps[i][0];
            int j1=pe.y+ps[i][1];
            if(i1<1||i1>n||j1<1||j1>m||pe.t==0)continue;
            if(s[i1][j1]=='g')continue;//容易忘！！！这个是关键，我当时忘了。减少时间复杂度。
            s[i1][j1]='g';
             q.push((Lawn){i1,j1,pe.t-1});
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        cout<<s[i][j];
        cout<<endl;
    }

    return 0;

}