世界上最快的排序算法——Timsort
Timsort
- 前言
- 简介
- 算法
- 限制
- 二分插入排序
- Run
- 合并
- 合并条件
- 合并内存消耗
- 加速合并
- GALLOP模式
- 总结
- 参考
前言
经过60多年的发展,科学家和工程师们发明了很多排序算法,有基本的插入算法,也有相对高效的归并排序算法等,他们各有各的特点,比如归并排序性能稳定、堆排序空间消耗小等等。但是这些算法也有自己的局限性比如快速排序最坏情况和冒泡算法一样,归并排序需要消耗的空间最多,插入排序平均情况的时间复杂度太高。在实际工程应用中,我们希望得到一款综合性能最好的排序算法,能够兼具最坏和最好时间复杂度(空间复杂度的优化可以靠后毕竟内存的价格是越来越便宜),于是基于归并和插入排序的TimSort就诞生了,并且被用作Java和Python的内置排序算法。
简介
Timsort是一个自适应的、混合的、稳定的排序算法,融合了归并算法和二分插入排序算法的精髓,在现实世界的数据中有着特别优秀的表现。它是由Tim Peter于2002年发明的,用在Python这个编程语言里面。这个算法之所以快,是因为它充分利用了现实世界的待排序数据里面,有很多子串是已经排好序的不需要再重新排序,利用这个特性并且加上合适的合并规则可以更加高效的排序剩下的待排序序列。
当Timsort运行在部分排序好的数组里面的时候,需要的比较次数要远小于 n l o g n nlogn nlogn,也是远小于相同情况下的归并排序算法需要的比较次数。但是和其他的归并排序算法一样,最坏情况下的时间复杂度是 O ( n l o g n ) O(nlogn) O(nlogn)的水平。但是在最坏的情况下,Timsort需要的临时存储空间只有 n / 2 n/2 n/2,在最好的情况下,需要的额外空间是常数级别的。从各个方面都能够击败需要 O ( n ) O(n) O(n)空间和稳定 O ( n l o g n ) O(nlogn) O(nlogn)时间的归并算法。
OK!结合精心制作的动图,让我们来看看这个牛皮的Timsort到底是怎么回事。
算法
限制
在最初的Tim实现的版本中,对于长度小于64数组直接进行二分插入排序,不会进行复杂的归并排序,因为在小数组中插入排序的性能已经足够好。在Java中有略微的改变,这个阈值被修改成了32,据说在实际中32这个阈值能够得到更好的性能。
二分插入排序
插入排序的逻辑是将排好序的数组之后的一个元素不停的向前移动交换元素直到找到合适的位置,如果这个新元素比前面的序列的最小的元素还要小,就要和前面的每个元素进行比较,浪费大量的时间在比较上面。采用二分搜索的方法直接找到这个元素应该插入的位置,就可以减少很多次的比较。虽然仍然是需要移动相同数量的元素,但是复制数组的时间消耗要小于元素间的一一互换。
比如对于[2,3,4,5,6,1],想把1插入到前面,如果使用直接的插入排序,需要5次比较,但是使用二分插入排序,只需要2次比较就直到插入的位置,然后直接把2,3,4,5,6全部向后移动一位,把1放入第一位就完成了插入操作。
Run
首先介绍其中最重要的一个概念,英文叫做run,翻译能力宕机的我就在这篇文章中用英文名字吧( ╯□╰ )。所谓的run就是一个连续上升(此处的上升包括两个元素相等的情况)或者下降(严格递减)的子串。
比如对于序列[1,2,3,4,3,2,4,7,8],其中有三个run,第一个是[1,2,3,4],第二个是[3,2],第三个是[4,7,8],这三个run都是单调的,在实际程序中对于单调递减的run会被反转成递增的序列。
在合并序列的时候,如果run的数量等于或者略小于2的幂次方的时候,效率是最高的;如果略大于2的幂次方,效率就会特别低。所以为了提高合并时候的效率,需要尽量控制每个run的长度,定义一个minrun表示每个run的最小长度,如果长度太短,就用二分插入排序把run后面的元素插入到前面的run里面。对于上面的例子,如果minrun=5,那么第一个run是不符合要求的,就会把后面的3插入到第一个run里面,变成[1,2,3,3,4]。
在执行排序算法之前,会计算出这个minrun的值(所以说这个算法是自适应的,会根据数据的特点来进行自我调整),minrun会从32到64(包括)选择一个数字,使得数组的长度除以minrun等于或者略小于2的幂次方。比如长度是65,那么minrun的值就是33;如果长度是165,minrun就是42(注意这里的Java的minrun的取值会在16到32之间)。
这里用Java源码做示范:
private static int minRunLength(int n) {
assert n >= 0;
int r = 0; // 如果低位任何一位是1,就会变成1
while (n >= 64) { // 改成了64
r |= (n & 1);
n >>= 1;
}
return n + r;
}
合并
在归并算法中合并是两两分别合并,第一个和第二个合并,第三个和第四个合并,然后再合并这两个已经合并的序列。但是在Timsort中,合并是连续的,每次计算出了一个run之后都有可能导致一次合并,这样的合并顺序能够在合并的同时保证算法的稳定性。
在Timsort中用一个栈来保存每个run,比如对于上面的[1,2,3,4,3,2,4,7,8]这个例子,栈底是[1,2,3,4],中间是[3,2],栈顶是[4,7,8],每次合并仅限于栈里面相邻的两个run。
合并条件
为了保证Timsort的合并平衡性,Tim制定一个合并规则,对于在栈顶的三个run,用X、Y和Z分别表示他们的长度,其中X在栈顶,必须始终维持一下的两个规则:
Z > Y + X Z > Y + X Z>Y+X
Y > X Y > X Y>X
一旦有其中的一个条件不被满足,Y这个子序列就会和X于Z中较小的元素合并形成一个新run,然后会再次检查栈顶的三个run看看是否仍然满足条件。如果不满足则会继续进行合并,直至栈顶的三个元素(如果只有两个run就只需要满足第二个条件)满足这两个条件。
图片来自这里
所谓的合并的平衡性就是为了让合并的两个数组的大小尽量接近,提高合并的效率。所以在合并的过程中需要尽量保留这些run用于发现后来的模式,但是我们又想尽量快的合并内存层级比较高的run,并且栈的空间是有限的,不能浪费太多的栈空间。通过以上的两个限制,可以将整个栈从底部到顶部的run的大小变成严格递减的,并且收敛速度和斐波那契数列一样,这样就可以应用斐波那契数列和的公式根据数组的长度计算出需要的栈的大小,一定是比 l o g 1.618 N log_{1.618}N log1.618N要小的,其中N是数组的长度。
在最理想的情况下,这个栈从底部到顶部的数字应该是128、64、32、16、8、4、2、2,这样从栈顶合并到栈底,每次合并的两个run的长度都是相等的,都是完美的合并。
如果遇到不完美的情况比如500、400、1000,那么根据规则就会合并变成900、1000,再次检查规则之后发现还是不满足,于是合并变成了1900。
合并内存消耗
不使用额外的内存合并两个run是很困难的,有这种原地合并算法,但是效率太低,作为trade-off,可以使用少量的内存空间来达到合并的目的。
比如有两个相邻的run一前一后分别是A和B,如果A的长度比较小,那么就把A复制到临时内存里面,然后从小到大开始合并排序放入A和B原来的空间里面不影响原来的数据的使用。如果B的长度比较小,B就会被放到临时内存里面,然后从大到小开始合并。
另外还有一个优化的点在于可以用二分法找到B[0]在A中应该插入的位置i以及A[A.length-1]在B中应该插入的位置j,这样在i之前和j之后的数据都可以放在原地不需要变化,进一步减小了A和B的大小,同时也是缩减了临时空间的大小。
加速合并
在归并排序算法中合并两个数组就是一一比较每个元素,把较小的放到相应的位置,然后比较下一个,这样有一个缺点就是如果A中如果有大量的元素A[i...j]是小于B中某一个元素B[k]的,程序仍然会持续的比较A[i...j]中的每一个元素和B[k],增加合并过程中的时间消耗。
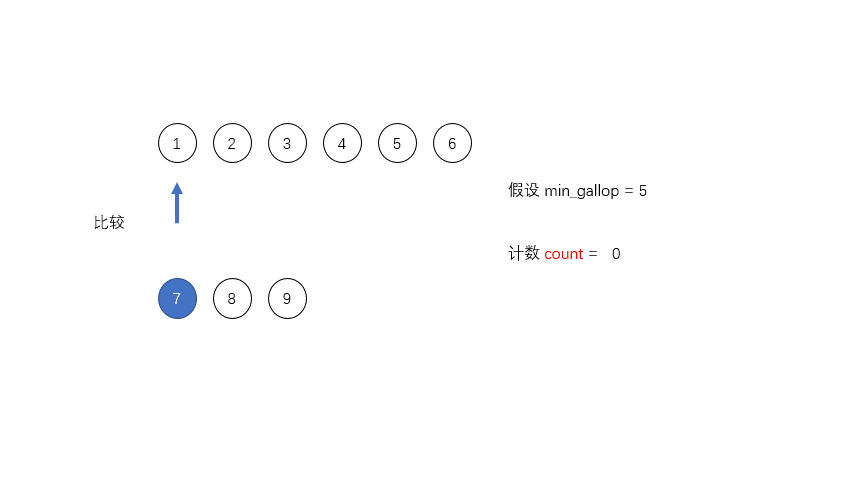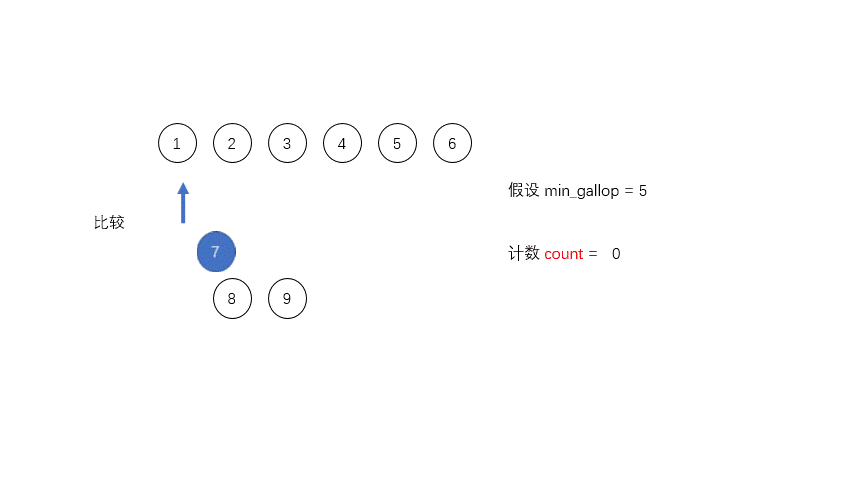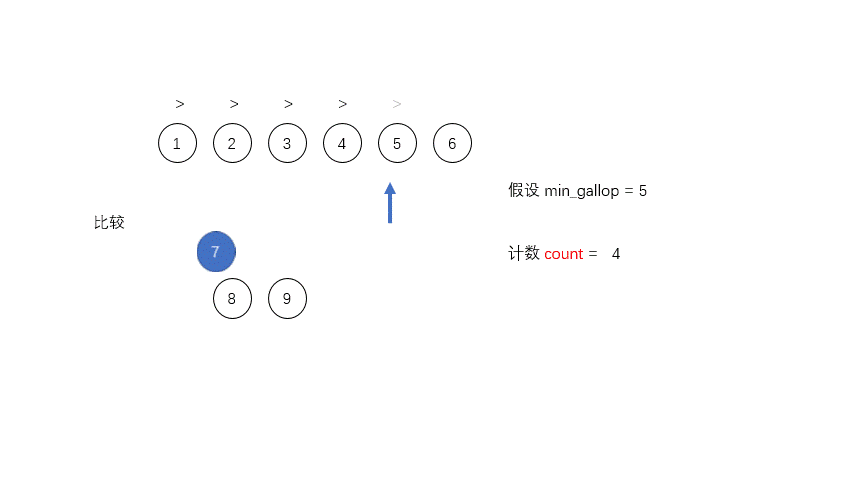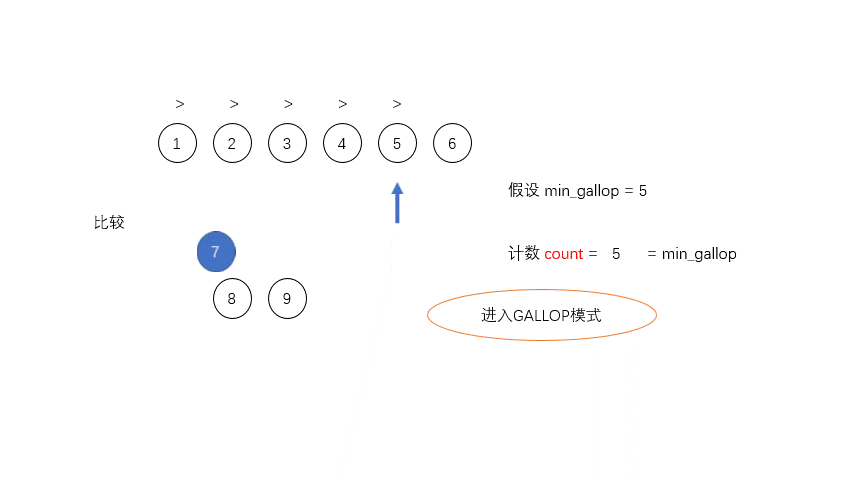
为了优化合并的过程,Tim设定了一个阈值MIN_GALLOP,如果A中连续MIN_GALLOP个元素比B中某一个元素要小,那么就进入GALLOP模式,反之亦然。默认的MIN_GALLOP值是7。
在GALLOP模式中,首先通过二分搜索找到A[0]在B中的位置i0,把B中i0之前的元素直接放入合并的空间中,然后再在A中找到B[i0]所在的位置j0,把A中j0之前的元素直接放入合并空间中,如此循环直至在A和B中每次找到的新的位置和原位置的差值是小于MIN_GALLOP的,这才停止然后继续进行一对一的比较。
GALLOP模式
GALLOP搜索元素分为两个步骤,比如我们想找到A中的元素x在B中的位置
第一步是在B中找到合适的索引区间 ( 2 k − 1 , 2 k + 1 − 1 ) (2^k-1,2^{k+1}-1) (2k−1,2k+1−1)使得x在这个元素的范围内
第二步是在第一步找到的范围内通过二分搜索来找到对应的位置。
通过这种搜索方式搜索序列B最多需要 2 l g B 2lgB 2lgB次的比较,相比于直接进行二分搜索的 l g ( B + 1 ) lg(B+1) lg(B+1)次比较,在数组长度比较短或者重复元素比较多的时候,这种搜索方式更加有优势。
这个搜索算法又叫做指数搜索(exponential search),在Peter McIlroy于1993年发明的一种乐观排序算法中首次提出的。
总结
总结一下上面的排序的过程:
- 如果长度小于
64直接进行插入排序 - 首先遍历数组收集每个元素根据特定的条件组成一个
run - 得到一个
run之后会把他放入栈中 - 如果栈顶部几个的
run符合合并条件,就会触发合并操作合并相邻的两个run留下一个run - 合并操作会使用尽量小的内存空间和GALLOP模式来加速合并
参考
Comparison between timsort and quicksort
This is the fastest sorting algorithm ever
TimSort
Timsort: The Fastest sorting algorithm for real-world problems
[Python-Dev] Sorting
Intro
TimSort
更多精彩内容请看我的个人博客