图的连通性问题之最小生成树:Prim算法_Kruskal算法(

目录

 

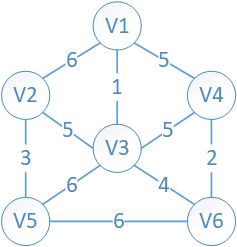
0.构造连通网的最小代价生成树（Minimun Cost Spanning Tree)，简称最小生成树。

1.求UDN的最小生成树Prim算法

2.Kruscal算法

2.1树的存储结构之双亲表示法

2.2树与等价问题：集合的树型结构表示：查找某个元素属于哪一个子集，合并两个非空子集；等价类划分

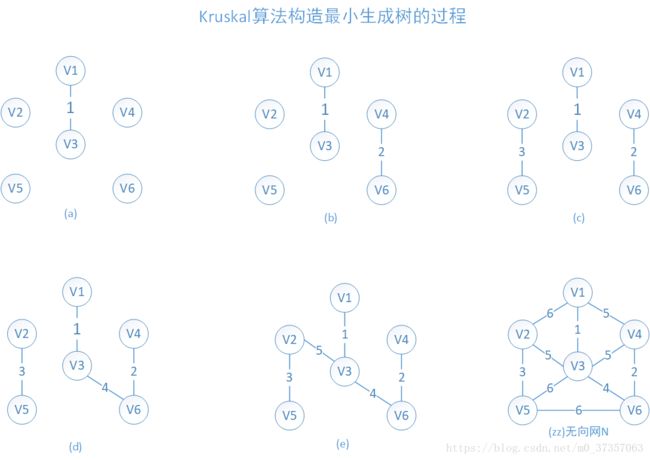
2.3求UDN的最小生成树之Kruscal算法

---

小结：

1.Prim算法使用了带权无向图（网）的邻接矩阵存储结构，辅助数组closedge的使用是关键！

2.Kruskal算法就较为难实现：要掌握好树的双亲表示法，用双亲表示法去实现集合的树型表示，并实现几个集合的操作！

另外要依据实例记录什么是等价问题，怎么划分等价类？树与等价类问题的关系！具体到图中就是区分结点属于哪一个连通分量！

3.Prim算法的时间复杂度O(n*n);Kruckal算法的时间复杂度O(eloge)，，其中n为图顶点个数，e为图中边的条数

0.构造连通网的最小代价生成树（Minimun Cost Spanning Tree)，简称最小生成树。

MST性质：

设N=（V，{E})是一个连通网络，U是顶点集合V的一个非空子集。若(u,v)是一条具有最小权值（代价)的边，其中u属于U，

v属于V-U，则必存在一棵包含边(u,v)的最小生成树。

 

1.求UDN的最小生成树Prim算法

设N=（V，{E}）是连通网，TE是N上最小生成树中边的集合(Tree Edge)。

Prim算法从U={u0}（u0属于V）,TE={}(空集合）开始，重复执行下列操作：

在所有u(u属于U），v（v属于V-U)的边(u,v) ((u,v)属于E）中找一条代价最小的边(u0,v0)并入集合TE,

同时v0并入U，

直至U=V为止。

此时TE中必有n-1条边，则T=(V,{TE})为N的最小生成树。

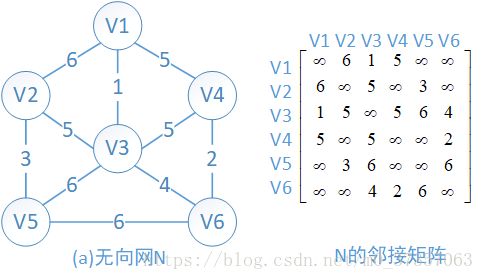
图的存储结构之数组表示法：

#define INFINITE INT_MAX
#define MAX_VERTEX_NUM 6

#define VRType int
#define VertexType int


typedef struct ArcCell{
	VRType adj;
}ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];

typedef struct{
	VertexType vexs[MAX_VERTEX_NUM];
	AdjMatrix arcs;
	int vexnum, arcnum;
}MGraph;
//sizeof(MGraph) = 176		44*4=176

 会采用数组（邻接矩阵）表示法，构造无向网UDN：

 

#define INFINITE INT_MAX
#define MAX_VERTEX_NUM 6

#define VRType int
#define VertexType int


typedef struct ArcCell{
	VRType adj;
}ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];

//AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];可以理解这个为ArcCell类型的二维结构体数组，数组的维度是指定好的！
//数组名AdjMatrix就是ArcCell类型的二维结构体数组的指针类型！

typedef struct{
	VertexType vexs[MAX_VERTEX_NUM];
	AdjMatrix arcs;
	int vexnum, arcnum;
}MGraph;
//sizeof(MGraph) = 176		44*4=176

 下面代码构造无向网UDN：

bool CreateUDN(MGraph& G)
{
	cin >> G.vexnum >> G.arcnum;
	for (int i = 0; i < G.vexnum; i++)
	{
		//cin >> G.vexs[i];
		G.vexs[i] = i;
	}
	//初始化邻接矩阵
	for (int i = 0; i < G.vexnum; i++)
	{
		for (int j = 0; j < G.vexnum; j++)
		{
			G.arcs[i][j] = { INFINITE };
		}
	}

	//构造邻接矩阵，输入一条边依附的顶点及权值
	for (int k = 0; k < G.arcnum; k++)
	{
		int v1, v2, w;//输入一条边依附的顶点及权值
		cin >> v1 >> v2 >> w;
		G.arcs[v1-1][v2-1].adj = w;
		G.arcs[v2-1][v1-1].adj = w;//设置的对弧
	}

	return true;
}//CreateUDN

Prim算法实现时的辅助数组：closedge:

typedef struct{
	VertexType adjvex;
	VRType lowcost;
}ClosEdge[MAX_VERTEX_NUM];

下面为Prim算法实现：

Prim算法的关键就是通过辅助数组closedge中元素中lowcost分量值是否为0来区分该节点是否是属于U，还是属于V-U；

第二个循环过程就是在closedge中查找lowcost分量最小的值，找到后并更新closedge数组的过程！

其中查找lowcost最小的代码在函数miniEdge()中实现：

int mimiEdge(ClosEdge& closedge)
{//在数组closedge中找分量lowcost>0且最小的那个元素
	VRType mini = INT_MAX;
	int index;
	for (int i = 0; i < MAX_VERTEX_NUM; i++)
	{
		if (closedge[i].lowcost >0 && closedge[i].lowcost < mini)
		{
			mini = closedge[i].lowcost;
			index = i;
		}
	}
	return index;
}

void MiniSpanTree_Prim(MGraph G, VertexType u, ClosEdge& closedge)
{
	int k = u-1;//k=LocateVex(u);
	for (int j = 0; j < G.vexnum; j++)
	{
		closedge[j] = { k, G.arcs[k][j].adj };
	}
	closedge[k].lowcost = 0;

	for (int i = 1; i < G.vexnum; i++)
	{
		int k = mimiEdge(closedge);
		cout << closedge[k].adjvex +1<< "->" << G.vexs[k] +1<< endl;//输出生成树的边
		closedge[k].lowcost = 0;
		for (int j = 0; j < G.vexnum; j++)
		{//更新closedge数组
			if (G.arcs[k][j].adj < closedge[j].lowcost)
			{
				closedge[j] = { G.vexs[k], G.arcs[k][j].adj };
			}
		}
	}
}//MiniSpanTree_Prim

下面是测试代码：

int _tmain(int argc, _TCHAR* argv[])
{
	MGraph G;
	cout << "sizeof(MGraph)=" << sizeof(MGraph) << endl;//sizeof(MGraph)=176
	CreateUDN(G);
	ClosEdge closedge;
	MiniSpanTree_Prim(G, 6, closedge);

	system("pause");
	return 0;
}

输入输出：

输入输出：（注：输入的顶点下标都是从1计起，即V1的下标就是1，而在程序里存储的下标都是0计起
输出的顶点也为了方便阅读，下标从1计起，即V1的编号为1
6 10
1 2 6
1 3 1
1 4 5
2 3 5
3 4 5
2 5 3
3 5 6
3 6 4
4 6 2
5 6 6
1->3
3->6
6->4
3->2
2->5
请按任意键继续. . .

2.Kruscal算法

2.1树的存储结构之双亲表示法

2.2树与等价问题：集合的树型结构表示：查找某个元素属于哪一个子集，合并两个非空子集；等价类划分

2.3求UDN的最小生成树之Kruscal算法

首先构造树的双亲表示法：（这里的树是广义树，不仅是二叉树）

树结点（顶点）;

typedef struct PTNode{
	int No;		//顶点编号
	int parent;//该结点双亲的位置域
}PTNode;

 下面的PTree类提供了依照树的双亲表示法，得到的几个的树型结点表示法，并提供了构造函数，析构函数，元素属于哪一个子集的查找函数fix_mfser()和两个非空子集的合并函数mix_mfset()以及，判断两个顶点是否属于同一集合（同一连通分量）的函数isEqualClass():

//typedef PTree MFSet;
class PTree{
public:
	vector nodes;
	int root;//根的位置
	int n;	//结点数目

	PTree(int vexNum)
	{
		n = vexNum;
		for (int i = 0; i < n; i++)
		{
			PTNode* ptnodePtr = new PTNode;
			ptnodePtr->No = i;
			ptnodePtr->parent = -1;
			nodes.push_back(ptnodePtr);
		}
	}
	~PTree()
	{
		for (int i = 0; i < n; i++)
		{
			delete nodes[i];
			nodes[i] = nullptr;
		}
	}

	int fix_mfset(int i)//查找i所在子集合
	{//确定i所在子集合，并把从i至根路径上所以结点都变成根的孩子结点
		if (i<0 || i>n-1)
		{
			return -1;
		}
		int j, k,t;
		for (j = i; nodes[j]->parent >= 0; j = nodes[j]->parent);//注意：下标从0计算起，所以nodes[j]->parent >= 0  
		for (k = i; k != j; k = t)
		{
			t = nodes[k]->parent;
			nodes[k]->parent = j;
		}
		return j;
	}

	void mix_mfset(int i, int j)
	{//nodes[i]和node[j]分别为集合S的互不相交的两个子集Si和Sj的根结点。
		if (i<0 || i>n-1 || j<0 || j>n-1)
		{
			throw new std::invalid_argument("mix_mfset()参数错误");
		}
		if (nodes[i]->parent > nodes[j]->parent)
		{
			nodes[j]->parent += (nodes[i]->parent);
			nodes[i]->parent = j;
		}
		else
		{
			nodes[i]->parent += (nodes[j]->parent);
			nodes[j]->parent = i;
		}
	}

	bool isEqualClass(int i, int j)
	{
		return (fix_mfset(i) == fix_mfset(j));
	}
};

下面是无向网边的结构定义：

typedef struct Edge{
	int vex1, vex2;
	int weight;
}Edge;

下面是无向网类的定义:

class UDN
{
public:
	int vexnum, arcnum;
	//vector vexPtrVec;
	PTree* ptree;
	vector edgePtrVec;
	priority_queue, edgePtrQueue_SortRule> edgePtrQueue;
	//优先队列内部自动用堆排序，使用top()、pop()函数实现元素的有序输出！存储结构时树（堆）的存储结构


	void printEdgeWeight(priority_queue, edgePtrQueue_SortRule> edgePtrQueue)
	{
		for (int i = 0; i < arcnum; i++)
		{
			Edge* edge = edgePtrQueue.top();
			edgePtrQueue.pop();
			cout << edge->weight << " ";
		}
		cout << endl;
	}


	bool CreateUDN()
	{
		cin >> vexnum >> arcnum;
		ptree = new PTree(vexnum);

		//for (int i = 0; i < udn.vexnum; i++)
		//{//这里可以输入每个顶点的信息！

		//}

		for (int i = 0; i < arcnum; i++)
		{
			int v1, v2, w;
			cin >> v1 >> v2 >> w;
			Edge* edgePtr = new Edge;
			edgePtr->vex1 = v1 - 1;
			edgePtr->vex2 = v2 - 1;
			edgePtr->weight = w;

			edgePtrVec.push_back(edgePtr);
			edgePtrQueue.push(edgePtr);
		}
		return true;
	}

	bool DestroyUDN()
	{
		delete ptree;
		ptree = nullptr;
		for (int i = 0; i < arcnum; i++)
		{
			delete edgePtrVec[i];
		}
		edgePtrVec.clear();
		//delete &udn;//这条语句报错！
		return true;
	}

	vector MiniSpanTree_Kruscal()
	{//miniTree里存储最小生成树的边边集合的指针
		vector  miniSpanTree;

		while ( !edgePtrQueue.empty())
		{
			Edge* edge = edgePtrQueue.top();
			edgePtrQueue.pop();
			int v1, v2;
			v1 = edge->vex1;
			v2 = edge->vex2;
			
			//if (!ptree->isEqualClass(v1, v2))
			//{//这里有一个合并集合时概念的错误！，下面进行纠正！
			//	ptree->mix_mfset(v1, v2);//不是合并v1和v2这两个结点！，
			//	miniSpanTree.push_back(edge);
			//}
			if (!ptree->isEqualClass(v1, v2))
			{
				ptree->mix_mfset(ptree->fix_mfset(v1), ptree->fix_mfset(v2));//而是合并v1和v2所属集合的根节点！合并的时候通过根节点进行合并！
				miniSpanTree.push_back(edge);
			}


		}
		return miniSpanTree;
	}

	void printMiniSpanTree(vector edgeVec)
	{
		for (int i = 0; i < edgeVec.size(); i++)
		{
			cout << edgeVec[i]->vex1 + 1 << "->" << edgeVec[i]->vex2 + 1 << endl;
		}
	}

};

UDN类中有一个存储边的指针的优先队列，起排序规则如下仿函数：即依据边的权值升序排序：

class edgePtrQueue_SortRule
{//边的权值优先队列排序规则类(仿函数）
public:
	bool operator()(Edge* e1, Edge* e2)
	{
		return (e1->weight > e2->weight);
	}
};

UDN类中提供了构造无向网：CreateUDN()、析构无向网DestroyUDN()

和利用kruskal算法求该无向网的最小生成树的方法：vector MiniSpanTree_Kruscal()

以及打印所得最小生成树边的方法：void printMiniSpanTree(vector edgeVec)

 

下面是测试结果：

#include "stdafx.h"
#include
#include
#include

using namespace std;

int _tmain(int argc, _TCHAR* argv[])
{
	UDN udn;

	udn.CreateUDN();

	//udn.printEdgeWeight(udn.edgePtrQueue);

	vector miniSpanTreeEdge;
	miniSpanTreeEdge = udn.MiniSpanTree_Kruscal();
	udn.printMiniSpanTree(miniSpanTreeEdge);
	miniSpanTreeEdge.clear();


	udn.DestroyUDN();

	system("pause");
	return 0;
}

输入输出：

输入输出：
6 10
1 2 6
1 3 1
1 4 5
2 3 5
3 4 5
2 5 3
3 5 6
3 6 4
4 6 2
5 6 6
1->3
4->6
2->5
3->6
2->3
请按任意键继续. . .

 

 

参考资料：

[1]//参考《数据结构C语言版（第三版）P176 Kruskal算法和 P139树与等价问题，树的双亲表示法，集合的树型结构表示，集合的并操作，元素属于哪一个集合的查找操作！

带权图的最小生成树 

Prim算法

Kruskal算法

树与等价类问题

小结：

1.Prim算法使用了带权无向图（网）的邻接矩阵存储结构，辅助数组closedge的使用是关键！

2.Kruskal算法就较为难实现：要掌握好树的双亲表示法，用双亲表示法去实现集合的树型表示，并实现几个集合的操作！

另外要依据实例记录什么是等价问题，怎么划分等价类？树与等价类问题的关系！具体到图中就是区分结点属于哪一个连通分量！