红黑树、2-3树、B-树、B+树、B*树概念整理
红黑树
红黑树是在普通二叉树上,对没个节点添加一个颜色属性形成的,红黑树需要满足以下五条性质:
1.每一个结点有两种颜色属性:红和黑
2.根结点永远是黑色的
3.所有叶结点都是黑色的(NIL结点,但 Java 实现的红黑树将使用 null 来代表空节点,因此遍历红黑树时将看不到黑色的叶子节点,反而看到每个叶子节点都是红色的。)
![]()
4.每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
就是连续的两个节点不能是连续的红色,连续的两个节点的意思就是父节点与子节点不能是连续的红色。
5.任意结点到叶子结点经过的黑色结点的数目是一致的
2-3树
2-3树是最简单的B-树(或-树)结构,其每个非叶节点都有两个或三个子女,而且所有叶都在统一层上。2-3树不是二叉树,其节点可拥有3个孩子。不过,2-3树与满二叉树相似。
概念:
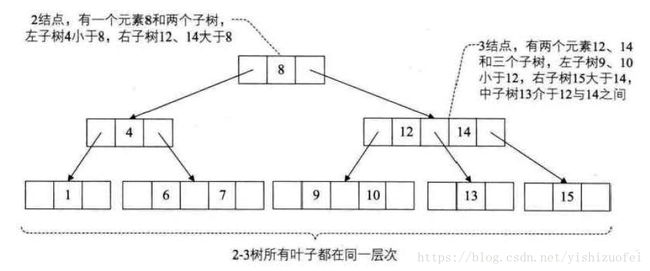
1、2-3树是这样的一棵多路查找树:其中的每一个结点都具有两个孩子(我们称它为2结点)或三个孩子(我们称它为3结点)。
2、一个2结点包含一个元素和两个孩子(或没有孩子),且与二叉排序树类似,左子树包含的元素小于该元素,右子树包含的元素大于该元素。不过,与二叉排序树不同的是,这个2结点要么没有孩子,要有就有两个,不能只有一个孩子。
3、一个3结点包含一小一大两个元素和三个孩子(或没有孩子),一个3结点要么没有孩子,要么具有3个孩子。如果某个3结点有孩子的话,左子树包含小于较小元素的元素,右子树包含大于较大元素的元素,中间子树包含介于两元素之间的元素。
2-3-4树
2-3-4树是2-3树的概念扩展,包括了4结点的使用。一个4结点包含小中大三个元素和四个孩子(或没有孩子),一个4结点要么没有孩子,要么具有4个孩子。如果某个4结点右孩子的话,左子树包含小于最小元素的元素;第二个子树包含大于最小元素,小于第二元素的元素;第三字数包含书大于第二元素,小于最大元素的元素;右子树包含大于最大元素的元素。
B-树
(注意这不是B减树,也根本没有B减树,这只是一个“-”,这就是B树)B树是一种平衡的多路查找树,2-3树和2-3-4树都是B树的特例。结点最大的孩子数目称为B树的阶,因此2-3树是3阶B树,2-3-4树是4阶B树。
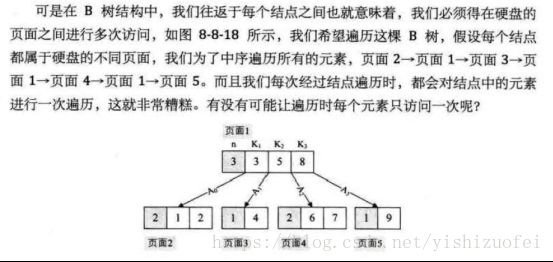
三阶B-树
![]()
B-树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点;
B+树
B+树是B-树的变体,也是一种多路搜索树:
1.其定义基本与B-树同,除了:
2.非叶子结点的子树指针与关键字个数相同;
3.非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树
(B-树是开区间);
5.为所有叶子结点增加一个链指针;
6.所有关键字都在叶子结点出现;
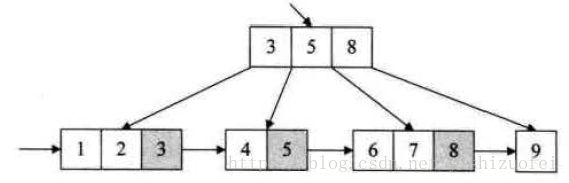
![]()
B+的特性:
1.所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好
是有序的;
2.不可能在非叶子结点命中;
3.非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储
(关键字)数据的数据层;
4.更适合文件索引系统;
对于树结构来说,我们都可以通过中序遍历来顺序查找树中的元素,这一切都是在内存中进行。
B-树和B+树的区别
如果要随机查找,我们就从根结点出发,与B树的查找的方式不同,只不过即使在分支结点找到了待查找的关键字,它也只是用来索引的,不能提供实际记录的访问,还是需要到达包含此关键字的终端结点。
如果我们是需要从最小关键字进行从小到大的顺序查找,我们就可以从最左侧的叶子结点出发,不经过分支结点,而是延着指向下一叶子的指针就可遍历所有的关键字。 
B/B+树通过对每个节点存储个数的扩展,使得对连续的数据能够进行较快的定位和访问,能够有效减少查找时间,提高存储的空间局部性从而减少IO操作。他广泛用于文件系统及数据库中,如:
Windows:HPFS文件系统
Mac:HFS,HFS+文件系统
Linux:ResiserFS,XFS,Ext3FS,JFS文件系统
数据库:ORACLE,MYSQL,SQLSERVER等中
根据B+树的结构,我们可以发现B+树相比于B树,在文件系统,数据库系统当中,更有优势,原因如下:
1、B+树的磁盘读写代价更低
B+树的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B树更小。如果把所有同一内部结点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说I/O读写次数也就降低了。
举个例子,假设磁盘中的一个盘块容纳16bytes,而一个关键字2bytes,一个关键字具体信息指针2bytes。一棵9阶B-tree(一个结点最多8个关键字)的内部结点需要2个盘快。而B+ 树内部结点只需要1个盘快。当需要把内部结点读入内存中的时候,B 树就比B+ 树多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。
2、B+树的查询效率更加稳定
由于内部结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。
2、B+树更有利于对数据库的扫描
B树在提高了磁盘IO性能的同时并没有解决元素遍历的效率低下的问题,而B+树只需要遍历叶子节点就可以解决对全部关键字信息的扫描,所以对于数据库中频繁使用的range query,B+树有着更高的性能。
B*树
![]()
是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针;
B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3(代替B+树的1/2);
B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针。
B*树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针。
所以,B*树分配新结点的概率比B+树要低,空间使用率更高。
总结:

参考资料:
https://blog.csdn.net/Sun_TTTT/article/details/65445754(最容易懂的红黑树)
https://blog.csdn.net/yishizuofei/article/details/81660841(多路查找树:2-3树、2-3-4树、B树、B+树、B*树、R树)
https://blog.csdn.net/u013411246/article/details/81088914(B树、B-树、B+树、B*树之间的关系)
https://blog.csdn.net/aqzwss/article/details/53074186(B-树,B+树,B*树详解)