线性表(部分)
从本节到接下来的几节讨论的线性表、栈、队列、串和数组都属于线性结构。线性结构的基本特点是除第一个元素无直接前驱,最后一个元素无直接后继之外,其他每个数据元素都有一个前驱和后继。
1.1 线性表的定义和特点
同一线性表中的元素必定具有相同的特性,即属于同一数据对象,相邻数据元素之间存在着序偶关系。
诸如此类由n(n>=0)个数据特性相同的元素构成的有限序列称为线性表。
- 线性表中元素的个数n(n>=0)定义为线性表的长度,n=0时称为空表。
对于非空的线性表或线性结构,其特点是:
- 存在唯一的一个被称作“第一个”的数据元素。
- 存在唯一的一个被称作“最后一个”的数据元素。
- 除第一个之外,结构中的每个数据元素均只有一个前驱。
- 除最后一个之外,结构中的每个数据元素均只有一个后继。
1.2 线性表的类型定义
下面给出线性表的抽象数据类型定义:
- 抽象数据类型仅是一个模型的定义,并不涉及模型的具体实现,因此这里描述中所涉及的参数不必考虑具体数据类型。
- 上述抽象数据类型中给出的操作只是基本操作,由这些基本操作可以构成其他较复杂的操作。
- 对于不同的应用,基本操作的接口可能不同。
- 由抽象数据类型定义的线性表,可以根据实际所采用的存储结构形式,进行具体的表示和实现。
1.3 线性表的顺序表示和实现
1.3.1 线性表的顺序存储表示
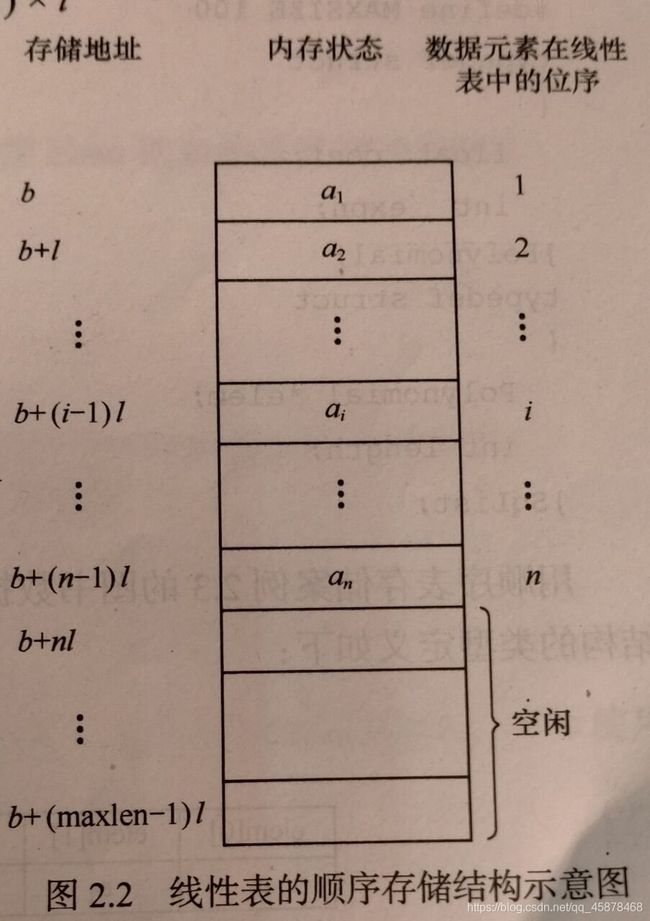
线性表的顺序表示指的是用一组地址连续的存储单元依次存储线性表的数据元素,这种表示也称作线性表的顺序存储结构或顺序映像。通常称这种存储结构的线性表为顺序表(Sequential List)。其特点是,逻辑上相邻的数据元素,其物理次序也是相邻的。
- LOC(a1)是线性表的第一个数据元素a1 的存储位置,通常称作线性表的起始位置或基地址。
- 线性表的顺序存储结构是一种随机可取的存储结构。
通常都用数组来描述数据结构中的顺序存储结构。在C语言中可用动态分配的一维数组表示线性表,描述如下:
//- - - - -顺序表的存储结构- - - - -
#define MAXSIZE 100 //顺序表可能达到的最大长度
typedef struct
{
ElemType *elem; //存储空间的基地址
int length; //当前长度
}SqList; //顺序表的结构类型为SqListlength表示顺序表中当前数据元素的个数。因为C语言数组的下标是从0开始的,而位置序号是从1开始的,所以要注意区分元素的位置序号和该元素在数组中的下标位置之间的对应关系。
#define MAXSIZE 100 //多项式可能达到的最大长度
typedef strust //多项式非零项的定义
{
float coef; //系数
int expn; //指数
}Polynomial;
typedef struct
{
Polynomial *elem; //存储空间的基地址
int length; //多项式中当前项的个数
}SqList; //多项式的顺序存储结构类型为SqList1.3.2顺序表中基本操作的实现
- 初始化
顺序表的初始化操作就是构造一个空的顺序表。
Status InitList(SqList &L)
{//构造一个空的顺序表L
L.elem=new ElemType[MAXSIZE]; //为顺序表分配一个大小为MAXSIZE的数组空间
if(!L.elem) exit(OVERFLOW); //存储分配失败退出
L.length=0; //空表长度为0
return OK;
}- 取值
取值操作是根据指定的位置序号i,获取顺序表中第i个数据元素的值。
Status GetElem(SqList L,int i,ElemType &e)
{
if(i<1||i>L.length) return ERROR; //判断i值是否合理,若不合理,返回ERROR
e=L.elem[i-1]; //elem[i-1]单元存储第i个数据元素
return OK;
}顺序表取值算法的时间复杂度为O(1)。
- 查找
查找操作是根据指定的元素值e,查找顺序表中第1个与e相等的元素。若查找成功,则返回该元素在表中的位置序号;若查找失败,则返回0。
int LocateElem(SqList L,ElemType e)
{//在顺序表L中查找值为e的数据元素,返回其序号
for(i=0;i长度为n的线性表中,顺序表按值查找算法的平均时间复杂度为O(n)。
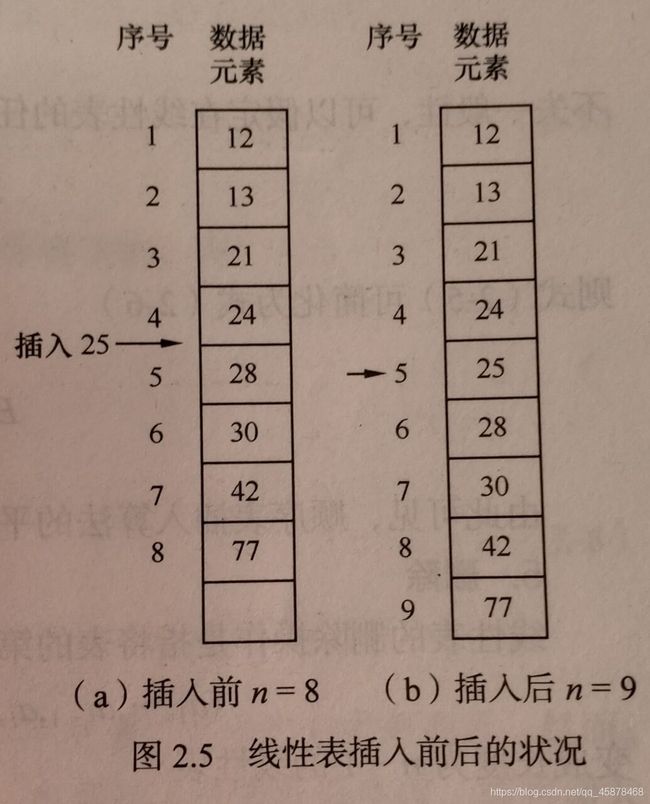
- 插入
线性表的插入操作是指在表的第i个位置插入一个新的数据元素e,使长度为n的线性表变为长度为n+1的线性表。
Status ListInsert(SqList &L,int i,ElemType e)
{//在顺序表L中第i个位置之前插入新的元素e,i值的合法范围是1<=i<=L.length+1
if((i<1)||(i>L.length+1)) return ERROR; //i值不合法
if(L.length==MAXSIZE) return ERROR; //当前存储空间已满
for(j=L.length-1;j>=i-1;j--)
L.elem[j+1]=L.elem[j]; //插入元素及之后的元素后移
L.elem[i-1]=e; //将新元素e放入第i个位置
++L.length; //表长加1
return OK;
}长度为n的线性表中,顺序表插入算法的平均时间复杂度为O(n)。
- 删除
线性表的删除操作是指将表的第i个元素删去,将长度为n的线性表变成长度为n-1的线性表。
Status ListDelete(SqList &L,int i)
{//在顺序表L中删除第i个元素,i值的合法范围是1<=i<=L.length
if((i<1)||(i>L.length)) return ERROR; //i值不合法
for(j=i;j<=L.length-1;j++)
L.elem[j-1]=L.elem[j]; //被删除元素之后的元素前移
--L.length; //表长减1
return OK;
}长度为n的线性表中,顺序表删除算法的平均时间复杂度为O(n)。