图论复习查漏补缺

1.若无向图G =（V，E）中含10个顶点，要保证图G在任何情况下都是连通的，则需要的边数最少是：37 (3分)

1. 45
2. 37
3. 36
4. 9

要想保证无向图G在任何情况下都是连通的，即任意变动图G中的边，G始终保持连通。首先需要图G的任意9（10-1）个结点构成完全连通子图G1（保证最大连通子图是个完全图），需n(n-1)/2=9×(9-1)/2=36条边，然后再添加一条边将第10个结点与G1连接起来，共37条边。
本题非常容易错误地选择选项A，主要原因是对“保证图G在任何情况下都是连通的”的理解，分析选项A，在图G中，具有10个顶点9条边并不能保证其一定是连通图，即有n-1条边的图不一定是连通图。（一定要注意是任何情况下）

2.如果G是一个有36条边的非连通无向图，那么该图顶点个数最少为多少？10(3分)

1. 7
2. 8
3. 9
4. 10

因为G为非连通图，所以G中至少含有两个连通子图，由于题目问至少有几个顶点，而且该图不含自回路和多重边，所以一个连通图可看成是一个点构成，另一个连通图可看成是一个完全图（因为完全图在最少顶点的情况下能得到的边数最多），这样该问题转化为这个36条边的完全图有多少个顶点，由公式可知：36＝n×（n-1）/2，则n＝9，加上另一个连通图（只有一个点），则图G至少有10个顶点.

这个题后面还有一堆几乎一样的，就是想清楚就好了

3.在N个顶点的无向图中，所有顶点的度之和不会超过顶点数的多少倍？N-1 (2分)

1. 1
2. 2
3. (N−1)/2
4. N−1

这个得分析，就是这种情况下只有是完全图的时候顶点度数之和才能最大，为N*（N-1），即顶点数乘以边数，而顶点数是N，所以一比就是N-1

4.对于一个具有N个顶点的无向图，要连通所有顶点至少需要多少条边？N−1 (2分)

1. N−1
2. N
3. N+1
4. N/2

这是个好题，可以和第一题来对比，这就是你不需要他什么时候都连通

只需要考虑他连通时最少的边数即可，很明显当围成一“圈”时最少

5.一个有N个顶点的强连通图至少有多少条边？N (2分)

1. N−1
2. N
3. N+1
4. N(N−1)

仔细想想，其实也就是绕“一圈”时最少

6.已知无向图G含有16条边，其中度为4的顶点个数为3，度为3的顶点个数为4，其他顶点的度均小于3。图G所含的顶点个数至少是：11(4分)

 

 

 

 7.

1. 10
2. 11
3. 13
4. 15
   16条边得出结点度数总和为32
   去除3个4度,4个3度,还剩8度
   因为题上说其余结点度数都小于3,所以度数最大为2
   所以最少还有4个结点,每个结点度数都为2
   4＋3＋4＝11

 .

一类题！！！

这种给你邻接矩阵或者邻接表的题唯一的步骤就是先画图，画对图就ok

最后一定要注意一点！！！

就是邻接表的每一行是有顺序的！！！从左到右遍历的（因为它本质上是一个单链表）

后面同类的就不解释了

8.

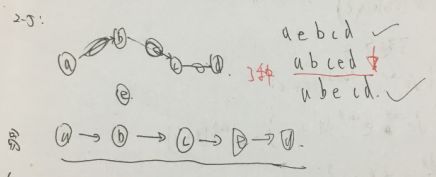
对下图进行拓扑排序，可以得到不同的拓扑序列的个数是：3 (2分)

 

1. 4
2. 3
3. 2
4. 1

这个我刚开始就漏了一种，一定要仔细并抓住拓扑排序的定义

9.

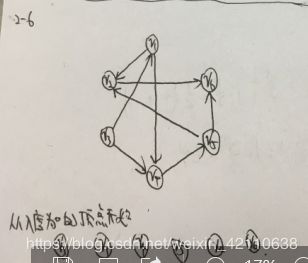
已知有向图G=(V, E)，其中V = {v1, v2, v3, v4, v5, v6}，E = {, , , , , , , }。G的拓扑序列是：A (2分)

 

1. v3, v1, v4, v5, v2, v6
2. v3, v4, v1, v5, v2, v6
3. v1, v3, v4, v5, v2, v6
4. v1, v4, v3, v5, v2, v6

画出来就ok了

 做拓扑排序的题要紧抓定义！！！

这也就是B错的原因 

 

10.2-31

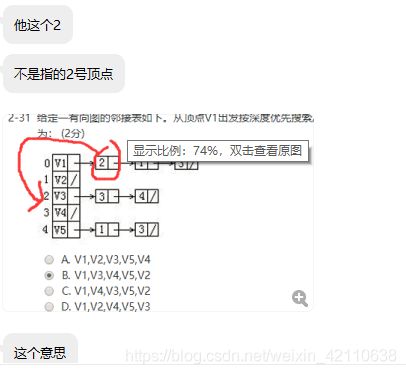
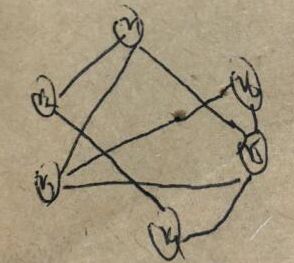
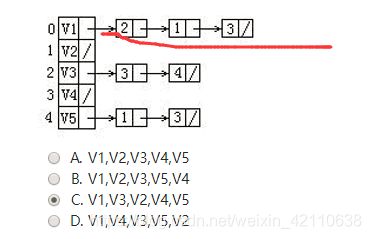
给定一有向图的邻接表如下。从顶点V1出发按深度优先搜索法进行遍历，则得到的一种顶点序列为： (2分)

V1,V2,V3,V5,V4 V1,V3,V4,V5,V2 V1,V4,V3,V5,V2 V1,V2,V4,V5,V3

这个题很容易错，其实思路和28是一样的，但是有几个地方需要注意

 

即V1指向3,2,4

还有a为什么不对，因为v3完了应该先是4而不是5，还是那个顺序的问题

还有如果这个图问你广搜，也就是2-38，也要注意这个入队出队的顺序！！！

2-32

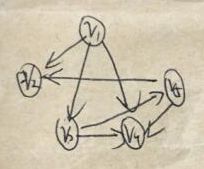
已知一个图的邻接矩阵如下，则从顶点V1出发按深度优先搜索法进行遍历，可能得到的一种顶点序列为： (2分)

作者: DS课程组

单位: 浙江大学

 

1. V1,V2,V3,V4,V5,V6
2. V1,V2,V4,V5,V6,V3
3. V1,V3,V5,V2,V4,V6
4. V1,V3,V5,V6,V4,V2

这种题也要画图，但是画图时有个技巧就是因为无向图的邻接矩阵是对称的，可以根据下三角就把图画出来

一定要注意d错的原因，默认从小到大去找

2-38

给定一有向图的邻接表如下。从顶点V1出发按广度优先搜索法进行遍历，则得到的一种顶点序列为： (2分)

 

 

 

1. V1,V2,V3,V4,V5
2. V1,V2,V3,V5,V4
3. V1,V3,V2,V4,V5
4. V1,V4,V3,V5,V2

同2-32，要注意a错的原因

 

你按这个顺序入队

那第二个出来的就应该是3

而不是2！！！