2020-08-13

禁忌搜索算法的感想

这段时间一直在学习禁忌搜索算法，为了能够验证算法，通过python书写了相关代码。根据CSDN上面一些博客，也是求解TSP问题。
禁忌搜索算法是局部搜索和爬山法的结合。运用了局部搜索的思想；再利用爬山法，保持最优解方向的迭代方向。减少循环次数，降低对解的要求，作为亚启发式算法，快速的找到最优解是其关键。
根据一些网课和博客的介绍，总结出禁忌搜索算法的关键步骤如下：
1、明确问题，找准目标函数。在算法实现过程中扮演着成本函数的作用。
2、初始解获取，禁忌搜索算法是基于一个可行解进行搜索的，获取一个优质的初始解极为重要。可先设计一个贪心算法进行初始解的获取。
3、解空间的编码，启发式算法主要用于NP难问题的求解。解的多维度以及解的数据类型存在差异，将解进行编码，让其适应于程序能够进行变换，才能更好的获取邻域。
4、禁忌表，禁忌对象。禁忌表用来存储禁忌对象，禁忌表需要是变动的，如果禁忌表是不变的，更容易陷入局部最优。禁忌对象是对解空间的一种约束，当禁忌对象进入禁忌表以后，解的搜寻将变得有方向。
5、禁忌步长、禁忌长度。禁忌步长是禁忌对象在禁忌表中停留的时间或者说次数。禁忌长度是禁忌表中存储的最多的禁忌对象的数量。用梯度下降的观点来看，禁忌步长相当于学习率。禁忌对象停留太短，不能尽快的达到最优，而禁忌对象停留得太长，则会导致迭代多次，浪费资源。禁忌长度则会直接的影响寻优的方向。禁忌长度太长，初始解的可搜索领域变小；太短，不能达到邻域搜索的目的。
6、特赦准则，禁忌搜索算法注重效率，当迭代一定次数后，选择一个次优的解作为其最优解。一般设置候选解，在候选解中选取，如果没有符合条件的，就选择初始解作为最优解。

下面是实现TSP问题求解的代码

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import random
import copy

#设置数据
np.random.seed(10000)
city_list = [[1, (1150.0, 1760.0)], [2, (630.0, 1660.0)], [3, (40.0, 2090.0)], [4,(750.0, 1100.0)],
              [5, (750.0, 2030.0)], [6, (1030.0, 2070.0)], [7, (1650.0, 650.0)], [8, (1490.0, 1630.0)],
              [9, (790.0, 2260.0)], [10, (710.0, 1310.0)], [11, (840.0, 550.0)], [12, (1170.0, 2300.0)],
              [13, (970.0, 1340.0)], [14, (510.0, 700.0)], [15, (750.0, 900.0)], [16, (1280.0, 1200.0)],
              [17,(230.0, 590.0)], [18, (460.0, 860.0)], [19, (1040.0, 950.0)], [20, (590.0, 1390.0)],
              [21, (830.0, 1770.0)], [22, (490.0, 500.0)], [23, (1840.0, 1240.0)], [24, (1260.0, 1500.0)],
              [25, (1280.0, 790.0)], [26, (490.0, 2130.0)], [27, (1460.0, 1420.0)], [28, (1260.0, 1910.0)],
              [29, (360.0, 1980.0)],[30,(1650.1,290.2)],[31,(650.2,390.6)],[32,(982.2,1802.5)]
             ]
#原始路径，序号代表先后顺序
origin = copy.deepcopy(city_list)
np.random.shuffle(origin) #打乱原始路径的序号，生成一条随机路径

#计算城市之间的距离
def city_distance(city1,city2):
    distance = np.sqrt(np.square(float(city1[1][0]-city2[1][0]))+np.square(float(city1[1][1]-city2[1][1])))
    return distance
#计算整条路线的总距离
def all_distance(origin):
    dis_list=[]
    citys = copy.deepcopy(origin)
    current_city = citys[0]
    citys.remove(current_city)
    sum_distance = 0
    while len(citys) >0:
        distance = city_distance(current_city,citys[0])
        dis_list.append(distance)
        sum_distance +=distance
        current_city = citys[0]
        citys.remove(current_city)
    oi_dis = city_distance(origin[-1],origin[0])
    dis_list.append(oi_dis)
    sum_distance = sum_distance+oi_dis
    return round(sum_distance,2),dis_list

#选出某城市邻居城市中，距离最短的城市
def short_distance(city1,city_list):
    now_min = 9999999999999
    now_city = None
    other_citys = copy.deepcopy(city_list)
    try:
        other_citys.remove(city1)
    except:
        print('没有当下城市')
    for i in range(len(other_citys)):
        distance = city_distance(city1,other_citys[i])
        if distance < now_min:
            now_min = distance
            now_city = other_citys[i]
    return now_min,now_city

#定义一个贪婪算法，获取一个较优的初始解,tsp问题，最直观的就是两两城市间距离最短进行连接
def greed_alg(sample_road,city_list):
    road = []
    copy_sample = copy.deepcopy(city_list)
    pre_city = sample_road[0]
    while len(copy_sample) >0:
        distance,next_city = short_distance(pre_city,copy_sample)
        road.append(pre_city)
        copy_sample.remove(pre_city)
        pre_city = next_city
    return road

def tab_search(origin,tab_step=100,tab_len=5,condidate_len=100,itertimes=1000):
    # 定义一个生产算子的函数，禁忌对象为地点的先后顺序，或者某两个位置的改变对于整体距离的影响。
    # 禁忌对象是基于初始解进行变换产生，而变换部分会产生禁忌对象。
    tabo_list = []  #禁忌表的构成为，1、固定两个城市的相邻关系，2、随机选定两个城市地点，保持其在系列中位置不变。
    original_road = greed_alg(sample_road=origin,city_list=city_list)
    original_cost,ver_distance= all_distance(original_road)
    aim_cost =  original_cost
    #创建一个列表，存储候选解
    condidate_jie = []
    condidate_cost = []
    condidate_jie.append(original_road)
    condidate_cost.append(original_cost)
    tab_step = 100 #禁忌步长为禁忌对象在禁忌表中迭代的次数，设置为100次
    #初始化禁忌表并添加第一个禁忌对象，
    def ori_init(original_road,t,condidate_cost=condidate_cost,condidate_jie=condidate_jie):
        new_road = copy.deepcopy(original_road)
        toa_dis,dis_list = all_distance(original_road)
        a = dis_list.index(min(dis_list))
        if a==dis_list.index(dis_list[-1]):
            a_value = original_road[a]
            b_value = original_road[0]
            new_road[a] = b_value
            new_road[0] = a_value
        else:
            a_value = original_road[a]
            b_value = original_road[a+1]
            new_road[a] = b_value
            new_road[a+1] = a_value
        new_toal_dis,dis_lis = all_distance(new_road)
        if new_toal_dis > toa_dis:
            tab_object = [(original_road[a],original_road[a+1]),t]
        else:
            condidate_cost.append(new_toal_dis)
            condidate_jie.append(new_road)
            tab_object = [(original_road[a+1], original_road[a]),t]
        return tab_object
    init_tab = ori_init(original_road,t=tab_step)
    tabo_list.append(init_tab)

    def pan_move(a,b,road,tabo_list):     #判断生成的两个元素是否在禁忌表里
        for each in tabo_list:
            if road[a] in each[0] and road[b] in each[0]:
                result = True
                break
            else:
                result = False
        return result
        #为禁忌表添加禁忌对象
    def add_tab(object1,object2,t=tab_step,tab=tab_len,tabo_list=tabo_list):
        if len(tabo_list)>tab:
            del tabo_list[0]
        else:
            tabo_list.append([(object1,object2),t])

    def prodece_road(road):     #领域解产生，通过随机交换两个地点的位置，产生领域解。
        new_citys = copy.deepcopy(road)
        i = 1
        xishu_list = [i for i in range(len(city_list))]
        while i ==1:
            sample = random.sample(xishu_list,2)
            index_a = sample[0]
            index_b = sample[1]
            result = pan_move(index_a,index_b,road,tabo_list)
            if  not result:
                i = 0
        city_1 = road[index_a]
        city_2 = road[index_b]
        new_citys[index_a] = city_2
        new_citys[index_b] = city_1
        return index_a,index_b,new_citys

    def item_search(road=original_road,itera_time=itertimes,t=tab_step,tabo_list=tabo_list,condidate_cost=condidate_cost,condidate_jie=condidate_jie):
        use_road = copy.deepcopy(road)
        cost, dis_list = all_distance(use_road)
        for i in range(itera_time):         #在迭代次数内进行领域搜索
            index_a,index_b,new_road = prodece_road(road=use_road)
            new_cost,new_distances = all_distance(new_road)
            if new_cost < cost :        #如果新的解使得目标成本降低，将新的解加入到候选解集中
                condidate_cost.append(new_cost)
                condidate_jie.append(new_road)
                add_tab(new_road[index_a], new_road[index_b],t=tab_step)
                use_road = new_road
            for each in tabo_list:          #每一次迭代，禁忌对象的迭代次数减一
                each[1] -=1
                if each[1] <0:
                    tabo_list.remove(each)
            if len(condidate_cost)>condidate_len:       #候选解集的长度设置为100，超过后，将比较次的解排除
                indexs = condidate_cost.index(max(condidate_cost))
                del condidate_cost[indexs]
                del condidate_jie[indexs]

            if len(tabo_list) ==0:     #如果禁忌表轮空，意味着，在当下解的领域里，更优解不容易找到，重新初始化初始解和禁忌对象
                new_tab=ori_init(new_road,t)
                tabo_list.append(new_tab)

        if min(condidate_cost) < aim_cost:      #选优法则，在迭代完成后，若候选解比初始解更优，选择候选解作为最终解
            fil_index = condidate_cost.index(min(condidate_cost))
            finally_cost = condidate_cost[fil_index]
            finally_jie = condidate_jie[fil_index]
        else:
            finally_cost = aim_cost
            finally_jie = original_road
        return finally_cost,finally_jie

    finally_distance,finally_road=item_search()
    return finally_road,finally_distance,

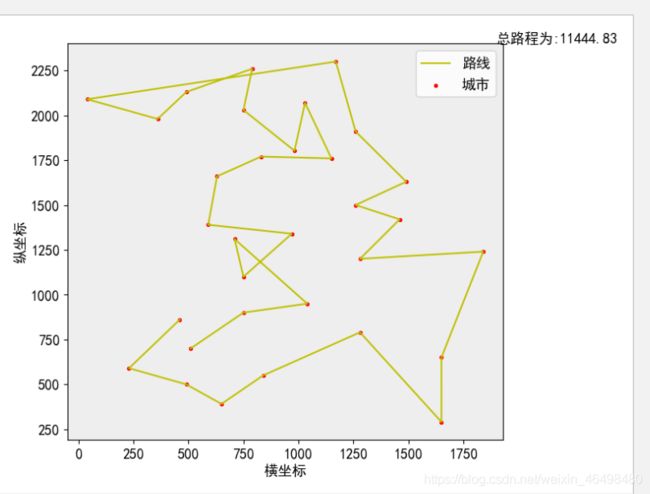
def picture(road,cost):
    mpl.rcParams['font.family'] = 'SimHei'  # 设置西文字体
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 设置正常显示中文字体
    mpl.rcParams['font.style'] = 'oblique'  # 设置字体风格
    mpl.rcParams['font.size'] = 13  # 设置字体大小
    x = []
    y = []
    for each in road:
        x.append(each[1][0])
        y.append((each[1][1]))
    figer = plt.figure(figsize=(8, 6))
    axes = figer.add_subplot(1, 1, 1, facecolor='#eeeeee')
    axes.scatter(x, y, marker='.', label='城市', s=30, color='r')
    axes.plot(x,y,'y-',label='路线',linewidth=1.5)
    axes.set_xlabel('横坐标')
    axes.set_ylabel('纵坐标')
    axes.legend()
    plt.text(x=1900,y=2400,s='总路程为:{}'.format(cost))
    plt.show()

if __name__ == '__main__':
    fina_road,fina_cost=tab_search(origin, tab_step=100, tab_len=5, condidate_len=100,itertimes=10000)
    picture(road=fina_road, cost=fina_cost)
    print(fina_cost)
    print(fina_road)
    print(all_distance(greed_alg(sample_road=origin,city_list=city_list))[0])   #贪心算法的总路程

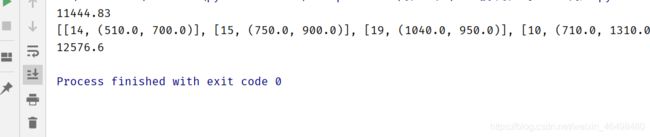
代码运行结果如下：

有兴趣的朋友们可以复制代码进行运行。欢迎指出错误。

说明

如果有用禁忌搜索算法实行其他问题求解的大佬愿意分享我们评论见。

文章的数据来源其他博客，代码的编写思路也有一定的模仿。附参考文章链接
参考博客地址一：禁忌搜索(Tabu Search)算法及python实现
参考博客地址二：禁忌搜索算法的实现_Python