使用 Caffe Python 编写 LeNet
使用 Caffe Python 编写 LeNet
前言:
本文翻译自 Solving in Python with LeNet,基于深度学习框架 Caffe 的应用,运行本代码的前提是:
安装了Caffe,windows Caffe安装教程以及添加Python接口请参考Caffe安装 和编译Caffe Python接口
安装 Python 2.7,推荐使用Anaconda安装。安装完以后启动Jupyter Notebook
注:为正确运行程序,本文代码对原文代码有改动。
还有,代码中的细节我会在详解目录中陆续更新
详解目录
- caffe.NetSpec()
- Caffe solver.net.forward(),solver.test_nets[0].forward() 和 solver.step(1)
正文:
1. 开始 (Setup)
导入 pylab,画图使用。
from pylab import *导入 caffe,添加系统变量。
caffe_root = 'D:/wincaffe/caffe-master/' # 这是我的caffe 根目录
import sys
sys.path.insert(0, caffe_root + 'python')
import caffe下载数据,下载好的数据请放在 D:\wincaffe\caffe-master\examples\mnist\mnist_data 目录下,我使用的是绝对路径。mnist 二进制文件需要转换为lmdb格式,我将原mnist文件和 lmdb 文件放在百度网盘mnist+lmdb (密码:h7wh)上了,不会转换的可以下载。 
2.创建网络(Creating the net)
现在我们创建一个源自1989年的经典卷积网络结构 LeNet 的变体。
我们需要两个额外的文件方便输出:
- net prototxt:定义了指向 train/test 数据的网络结构。
- solver prototxt : 定义了网络学习参数。
from caffe import layers as L, params as P
def lenet(lmdb, batch_size):
# our version of LeNet: a series of linear and simple nonlinear transformations
n = caffe.NetSpec() # 见详解目录-1
n.data, n.label = L.Data(batch_size=batch_size, backend=P.Data.LMDB, source=lmdb,
transform_param=dict(scale=1./255), ntop=2)
n.conv1 = L.Convolution(n.data, kernel_size=5, num_output=20, weight_filler=dict(type='xavier'))
n.pool1 = L.Pooling(n.conv1, kernel_size=2, stride=2, pool=P.Pooling.MAX)
n.conv2 = L.Convolution(n.pool1, kernel_size=5, num_output=50, weight_filler=dict(type='xavier'))
n.pool2 = L.Pooling(n.conv2, kernel_size=2, stride=2, pool=P.Pooling.MAX)
n.fc1 = L.InnerProduct(n.pool2, num_output=500, weight_filler=dict(type='xavier'))
n.relu1 = L.ReLU(n.fc1, in_place=True)
n.score = L.InnerProduct(n.relu1, num_output=10, weight_filler=dict(type='xavier'))
n.loss = L.SoftmaxWithLoss(n.score, n.label)
return n.to_proto() #写入到prototxt文件
with open('D:/wincaffe/caffe-master/examples/mnist/lenet_auto_train.prototxt', 'w') as f:
f.write(str(lenet('D:/wincaffe/caffe-master/examples/mnist/mnist_data/mnist_train_lmdb', 64)))
with open('D:/wincaffe/caffe-master/examples/mnist/lenet_auto_test.prototxt', 'w') as f:
f.write(str(lenet('D:/wincaffe/caffe-master/examples/mnist/mnist_data/mnist_test_lmdb', 100)))让我们看一下 train net 的结构:
layer {
name: "data"
type: "Data"
top: "data"
top: "label"
transform_param {
scale: 0.00392156862745
}
data_param {
source: "D:/wincaffe/caffe-master/examples/mnist/mnist_data/mnist_train_lmdb"
batch_size: 64
backend: LMDB
}
}
layer {
name: "conv1"
type: "Convolution"
bottom: "data"
top: "conv1"
convolution_param {
num_output: 20
kernel_size: 5
weight_filler {
type: "xavier"
}
}
}
layer {
name: "pool1"
type: "Pooling"
bottom: "conv1"
top: "pool1"
pooling_param {
pool: MAX
kernel_size: 2
stride: 2
}
}
layer {
name: "conv2"
type: "Convolution"
bottom: "pool1"
top: "conv2"
convolution_param {
num_output: 50
kernel_size: 5
weight_filler {
type: "xavier"
}
}
}
layer {
name: "pool2"
type: "Pooling"
bottom: "conv2"
top: "pool2"
pooling_param {
pool: MAX
kernel_size: 2
stride: 2
}
}
layer {
name: "fc1"
type: "InnerProduct"
bottom: "pool2"
top: "fc1"
inner_product_param {
num_output: 500
weight_filler {
type: "xavier"
}
}
}
layer {
name: "relu1"
type: "ReLU"
bottom: "fc1"
top: "fc1"
}
layer {
name: "score"
type: "InnerProduct"
bottom: "fc1"
top: "score"
inner_product_param {
num_output: 10
weight_filler {
type: "xavier"
}
}
}
layer {
name: "loss"
type: "SoftmaxWithLoss"
bottom: "score"
bottom: "label"
top: "loss"
}
还有 test net 的结构:
layer {
name: "data"
type: "Data"
top: "data"
top: "label"
transform_param {
scale: 0.00392156862745
}
data_param {
source: "D:/wincaffe/caffe-master/examples/mnist/mnist_data/mnist_test_lmdb"
batch_size: 100
backend: LMDB
}
}
layer {
name: "conv1"
type: "Convolution"
bottom: "data"
top: "conv1"
convolution_param {
num_output: 20
kernel_size: 5
weight_filler {
type: "xavier"
}
}
}
layer {
name: "pool1"
type: "Pooling"
bottom: "conv1"
top: "pool1"
pooling_param {
pool: MAX
kernel_size: 2
stride: 2
}
}
layer {
name: "conv2"
type: "Convolution"
bottom: "pool1"
top: "conv2"
convolution_param {
num_output: 50
kernel_size: 5
weight_filler {
type: "xavier"
}
}
}
layer {
name: "pool2"
type: "Pooling"
bottom: "conv2"
top: "pool2"
pooling_param {
pool: MAX
kernel_size: 2
stride: 2
}
}
layer {
name: "fc1"
type: "InnerProduct"
bottom: "pool2"
top: "fc1"
inner_product_param {
num_output: 500
weight_filler {
type: "xavier"
}
}
}
layer {
name: "relu1"
type: "ReLU"
bottom: "fc1"
top: "fc1"
}
layer {
name: "score"
type: "InnerProduct"
bottom: "fc1"
top: "score"
inner_product_param {
num_output: 10
weight_filler {
type: "xavier"
}
}
}
layer {
name: "loss"
type: "SoftmaxWithLoss"
bottom: "score"
bottom: "label"
top: "loss"
}
嗯,再给你看看solver的结构。这个文件在 D:\wincaffe\caffe-master\examples\mnist 中本来就存在。不过你需要根据路径自己修改一下代码中 train_net,test_net的路径。
# The train/test net protocol buffer definition
train_net: "D:/wincaffe/caffe-master/examples/mnist/lenet_auto_train.prototxt"
test_net: "D:/wincaffe/caffe-master/examples/mnist/lenet_auto_test.prototxt"
# test_iter specifies how many forward passes the test should carry out.
# In the case of MNIST, we have test batch size 100 and 100 test iterations,
# covering the full 10,000 testing images.
test_iter: 100
# Carry out testing every 500 training iterations.
test_interval: 500
# The base learning rate, momentum and the weight decay of the network.
base_lr: 0.01
momentum: 0.9
weight_decay: 0.0005
# The learning rate policy
lr_policy: "inv"
gamma: 0.0001
power: 0.75
# Display every 100 iterations
display: 100
# The maximum number of iterations
max_iter: 10000
# snapshot intermediate results
snapshot: 5000
snapshot_prefix: "mnist/lenet"
3.加载和验证solver(Loading and checking the solver)
译者注:选择设备和使用GPU。(没有安装CUDA+cuDnn的可以使用caffe.set_mode_cpu(),亲测,速度慢成屎。)
caffe.set_device(0) #选择默认gpu
caffe.set_mode_gpu() #使用gpu
### load the solver and create train and test nets
solver = None # ignore this workaround for lmdb data (can't instantiate two solvers on the same data)
solver = caffe.SGDSolver('C:/Users/Admin512/Desktop/MyStudy/caffe_python/LeNet/mnist/lenet_auto_solver.prototxt')看一下中间变量的维度:
代码1:
# each output is (batch size, feature dim, spatial dim)
[(k, v.data.shape) for k, v in solver.net.blobs.items()]输出1:
[('data', (64L, 1L, 28L, 28L)),
('label', (64L,)),
('conv1', (64L, 20L, 24L, 24L)),
('pool1', (64L, 20L, 12L, 12L)),
('conv2', (64L, 50L, 8L, 8L)),
('pool2', (64L, 50L, 4L, 4L)),
('fc1', (64L, 500L)),
('score', (64L, 10L)),
('loss', ())]代码2:
# just print the weight sizes (we'll omit the biases)
[(k, v[0].data.shape) for k, v in solver.net.params.items()]输出2:
[('conv1', (20, 1, 5, 5)),
('conv2', (50, 20, 5, 5)),
('fc1', (500, 800)),
('score', (10, 500))]训练前,让我们检查一下是否一切就绪:
代码1:
# 见详解目录-2
solver.net.forward() # train net
solver.test_nets[0].forward() # test net (there can be more than one)输出1:
{'loss': array(2.365971088409424, dtype=float32)}代码2:
# we use a little trick to tile the first eight images
imshow(solver.net.blobs['data'].data[:8, 0].transpose(1, 0, 2).reshape(28, 8*28), cmap='gray'); axis('off')
print 'train labels:', solver.net.blobs['label'].data[:8]输出2:
train labels: [ 5. 0. 4. 1. 9. 2. 1. 3.]代码3:
imshow(solver.test_nets[0].blobs['data'].data[:8, 0].transpose(1, 0, 2).reshape(28, 8*28), cmap='gray'); axis('off')
print 'test labels:', solver.test_nets[0].blobs['label'].data[:8]输出3:
test labels: [ 7. 2. 1. 0. 4. 1. 4. 9.]4.做一步solver(Stepping the solver)
训练网络和测试网看起来都在加载数据,并拥有正确的标签。
- 让我们做一步 minibatch-SGD ,看一下发生了什么:
# 见详解目录-2
solver.step(1)我们通过我们的滤波器(filters)进行了梯度传播吗?让我们看一下第一层的更新,这里展示了5×5的滤波器组成的4×5的网格。
代码4:
imshow(solver.net.params['conv1'][0].diff[:, 0].reshape(4, 5, 5, 5)
.transpose(0, 2, 1, 3).reshape(4*5, 5*5), cmap='gray'); axis('off')输出4:
(-0.5, 24.5, 19.5, -0.5)5.编写一个自定义的训练循环(Writing a custom training loop)
Something is happening. 我们让网络运行一段时间,运行期间我们保持跟踪一些事情。注意,这个过程和通过caffe二进制训练一样。特别是:
- 日志记录将继续正常进行。
- 在solver prototxt 指定的间隔获取快照(在这里,间隔取5000次迭代)
- 在指定的间隔进行测试(在这里,间隔取500次迭代)
因为我们可以使用 Python 控制循环,我们可以自由的计算额外的东西,就像下面展示的一样。我们也可以做一些别的事情,比如:
- 写一个自定义的停止标准
- 通过更新循环中的网络来改变求解过程
代码5:
%%time
niter = 200
test_interval = 25
# losses will also be stored in the log
train_loss = zeros(niter)
test_acc = zeros(int(np.ceil(niter / test_interval)))
output = zeros((niter, 8, 10))
# the main solver loop
for it in range(niter):
solver.step(1) # SGD by Caffe
# store the train loss
train_loss[it] = solver.net.blobs['loss'].data
# store the output on the first test batch
# (start the forward pass at conv1 to avoid loading new data)
solver.test_nets[0].forward(start='conv1')
output[it] = solver.test_nets[0].blobs['score'].data[:8]
# run a full test every so often
# (Caffe can also do this for us and write to a log, but we show here
# how to do it directly in Python, where more complicated things are easier.)
if it % test_interval == 0:
print 'Iteration', it, 'testing...'
correct = 0
for test_it in range(100):
solver.test_nets[0].forward()
correct += sum(solver.test_nets[0].blobs['score'].data.argmax(1)
== solver.test_nets[0].blobs['label'].data)
test_acc[it // test_interval] = correct / 1e4输出5:
(貌似我的GPU比他们的好不少!)
Iteration 0 testing...
Iteration 25 testing...
Iteration 50 testing...
Iteration 75 testing...
Iteration 100 testing...
Iteration 125 testing...
Iteration 150 testing...
Iteration 175 testing...
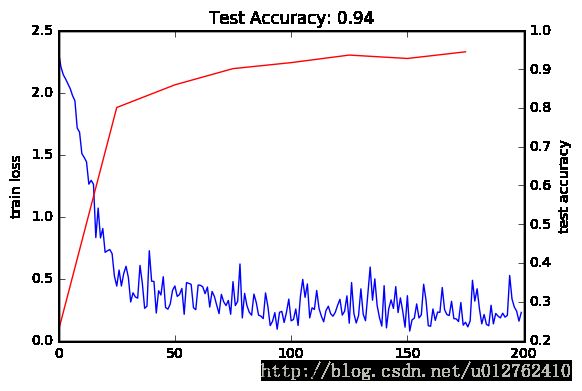
Wall time: 2.3 s我们看一下训练损失函数和测试正确率
代码6:
_, ax1 = subplots()
ax2 = ax1.twinx()
ax1.plot(arange(niter), train_loss)
ax2.plot(test_interval * arange(len(test_acc)), test_acc, 'r')
ax1.set_xlabel('iteration')
ax1.set_ylabel('train loss')
ax2.set_ylabel('test accuracy')
ax2.set_title('Test Accuracy: {:.2f}'.format(test_acc[-1]))输出6:
text.Text at 0x32b3fb38> 损失函数下降的很快,而且收敛(except for stochasticity,我觉得这句话翻译成除了局部随机性),相应的,正确率在上升。Hooray!
因为我们在第一次测试batch中保存了结果,所以我们可以观察我们的预测分数是如何演变的。x轴是迭代次数,y轴是标签。
代码7:
for i in range(8):
figure(figsize=(2, 2))
imshow(solver.test_nets[0].blobs['data'].data[i, 0], cmap='gray')
figure(figsize=(10, 2))
imshow(output[:50, i].T, interpolation='nearest', cmap='gray')
xlabel('iteration')
ylabel('label')输出7:
我们刚开始对这些数字(digit)一点都不了解,但是最后我们对每个数字都有正确的分类。随着分类的进行,你会发现识别最后的数字是非常困难的,倾斜的“9”很容易和“4”混淆。
注意:以上都是原始的输出而不是 softmax 计算的概率向量。如下所示,后者很容易表示我们的网络的 confidence (但是很难看到难以识别数字的分数)。
代码8:
for i in range(8):
figure(figsize=(2, 2))
imshow(solver.test_nets[0].blobs['data'].data[i, 0], cmap='gray')
figure(figsize=(10, 2))
imshow(exp(output[:50, i].T) / exp(output[:50, i].T).sum(0), interpolation='nearest', cmap='gray')
xlabel('iteration')
ylabel('label')####输出8:
6.网络结构和优化的实验(Experiment with architecture and optimization)
现在,我们已经定义,训练和测试了LeNet,下一步要做什么有很多可能的方向:
- 定义新的网络结构进行比较
- 通过设置 base_lr 和简单的训练更长的时间进行调优。
- 将 SGD 改成有适应能力的方法如 AdaDelta 或者 Adam
随意地通过编辑以下的多功能示例来探索这些方向。寻找“ EDIT HERE ”的注释所建议的修改要点。
默认情况下,它定义了一个简单的线性分类器作为基准。
In case your coffee hasn’t kicked in and you’d like inspiration, try out!!!
- 将 ReLU 转换为非线性的 ELU 或 Sigmoid 。
- 添加更多的连接和非线性层
- 以10×的倍数改变学习率
- 将solver type改为 Adam 。
- 将 niter 设置的更大让训练变得更长,让训练结果更好 。
代码9:
train_net_path = 'mnist/custom_auto_train.prototxt'
test_net_path = 'mnist/custom_auto_test.prototxt'
solver_config_path = 'mnist/custom_auto_solver.prototxt'
### define net
def custom_net(lmdb, batch_size):
# define your own net!
n = caffe.NetSpec()
# keep this data layer for all networks
n.data, n.label = L.Data(batch_size=batch_size, backend=P.Data.LMDB, source=lmdb,
transform_param=dict(scale=1./255), ntop=2)
# EDIT HERE to try different networks
# this single layer defines a simple linear classifier
# (in particular this defines a multiway logistic regression)
n.score = L.InnerProduct(n.data, num_output=10, weight_filler=dict(type='xavier'))
# EDIT HERE this is the LeNet variant we have already tried
# n.conv1 = L.Convolution(n.data, kernel_size=5, num_output=20, weight_filler=dict(type='xavier'))
# n.pool1 = L.Pooling(n.conv1, kernel_size=2, stride=2, pool=P.Pooling.MAX)
# n.conv2 = L.Convolution(n.pool1, kernel_size=5, num_output=50, weight_filler=dict(type='xavier'))
# n.pool2 = L.Pooling(n.conv2, kernel_size=2, stride=2, pool=P.Pooling.MAX)
# n.fc1 = L.InnerProduct(n.pool2, num_output=500, weight_filler=dict(type='xavier'))
# EDIT HERE consider L.ELU or L.Sigmoid for the nonlinearity
# n.relu1 = L.ReLU(n.fc1, in_place=True)
# n.score = L.InnerProduct(n.fc1, num_output=10, weight_filler=dict(type='xavier'))
# keep this loss layer for all networks
n.loss = L.SoftmaxWithLoss(n.score, n.label)
return n.to_proto()
with open(train_net_path, 'w') as f:
f.write(str(custom_net('mnist/mnist_train_lmdb', 64)))
with open(test_net_path, 'w') as f:
f.write(str(custom_net('mnist/mnist_test_lmdb', 100)))
### define solver
from caffe.proto import caffe_pb2
s = caffe_pb2.SolverParameter()
# Set a seed for reproducible experiments:
# this controls for randomization in training.
s.random_seed = 0xCAFFE
# Specify locations of the train and (maybe) test networks.
s.train_net = train_net_path
s.test_net.append(test_net_path)
s.test_interval = 500 # Test after every 500 training iterations.
s.test_iter.append(100) # Test on 100 batches each time we test.
s.max_iter = 10000 # no. of times to update the net (training iterations)
# EDIT HERE to try different solvers
# solver types include "SGD", "Adam", and "Nesterov" among others.
s.type = "SGD"
# Set the initial learning rate for SGD.
s.base_lr = 0.01 # EDIT HERE to try different learning rates
# Set momentum to accelerate learning by
# taking weighted average of current and previous updates.
s.momentum = 0.9
# Set weight decay to regularize and prevent overfitting
s.weight_decay = 5e-4
# Set `lr_policy` to define how the learning rate changes during training.
# This is the same policy as our default LeNet.
s.lr_policy = 'inv'
s.gamma = 0.0001
s.power = 0.75
# EDIT HERE to try the fixed rate (and compare with adaptive solvers)
# `fixed` is the simplest policy that keeps the learning rate constant.
# s.lr_policy = 'fixed'
# Display the current training loss and accuracy every 1000 iterations.
s.display = 1000
# Snapshots are files used to store networks we've trained.
# We'll snapshot every 5K iterations -- twice during training.
s.snapshot = 5000
s.snapshot_prefix = 'mnist/custom_net'
# Train on the GPU
s.solver_mode = caffe_pb2.SolverParameter.GPU
# Write the solver to a temporary file and return its filename.
with open(solver_config_path, 'w') as f:
f.write(str(s))
### load the solver and create train and test nets
solver = None # ignore this workaround for lmdb data (can't instantiate two solvers on the same data)
solver = caffe.get_solver(solver_config_path)
### solve
niter = 250 # EDIT HERE increase to train for longer
test_interval = niter / 10
# losses will also be stored in the log
train_loss = zeros(niter)
test_acc = zeros(int(np.ceil(niter / test_interval)))
# the main solver loop
for it in range(niter):
solver.step(1) # SGD by Caffe
# store the train loss
train_loss[it] = solver.net.blobs['loss'].data
# run a full test every so often
# (Caffe can also do this for us and write to a log, but we show here
# how to do it directly in Python, where more complicated things are easier.)
if it % test_interval == 0:
print 'Iteration', it, 'testing...'
correct = 0
for test_it in range(100):
solver.test_nets[0].forward()
correct += sum(solver.test_nets[0].blobs['score'].data.argmax(1)
== solver.test_nets[0].blobs['label'].data)
test_acc[it // test_interval] = correct / 1e4
_, ax1 = subplots()
ax2 = ax1.twinx()
ax1.plot(arange(niter), train_loss)
ax2.plot(test_interval * arange(len(test_acc)), test_acc, 'r')
ax1.set_xlabel('iteration')
ax1.set_ylabel('train loss')
ax2.set_ylabel('test accuracy')
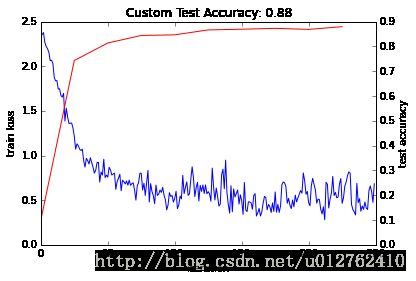
ax2.set_title('Custom Test Accuracy: {:.2f}'.format(test_acc[-1]))输出9:
Iteration 0 testing...
Iteration 25 testing...
Iteration 50 testing...
Iteration 75 testing...
Iteration 100 testing...
Iteration 125 testing...
Iteration 150 testing...
Iteration 175 testing...
Iteration 200 testing...
Iteration 225 testing...
<matplotlib.text.Text at 0x7f5199af9f50>