ndarray元素类型转换、shape变换、元素级运算、矩阵积
python高级应用与数据分析学习笔记 08
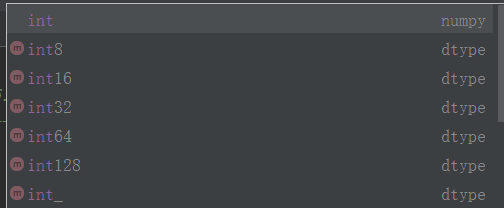
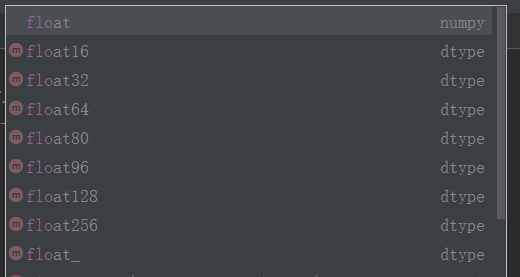
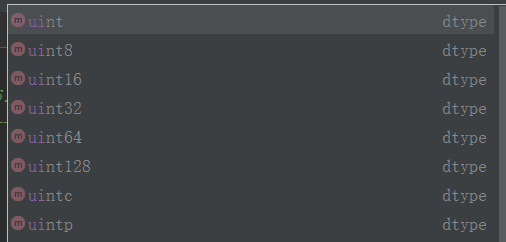
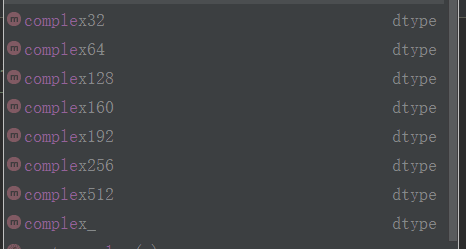
1、ndarray元素数据类型
int 类型
float 类型
uint类型
complex类型
string类型
object类型
unicode类型
boolen类型
2、ndarray元素类型转换:使用astype函数
a = np.array([1,2,4],dtype=np.bo)
print(a,a.dtype) #[1 2 4] int32
b = a.astype(np.string_)
print(b,b.dtype) #[b'1' b'2' b'4'] |S11
c = a.astype(np.str_)
print(c,c.dtype) #['1' '2' '4'] 'python','android','c','java'],dtype='U4')
print(d,d.dtype) #['pyth' 'andr' 'c' 'java'] 3、shape变换的两种方式
核心：size不变
三维数组（2,3,5） size = 2 * 3 * 5 = 30
转换成二维数组（3,10） size = 3 * 10 = 30
或者转换成二维数组（3,-1） 系统会自动计算：2 * 3 * 5 / 3 = 10
第一种方法：直接修改原数组
f = np.random.random((2,3,5))
print(f,f.shape)
# [[[ 0.47213292 0.14591814 0.59233384 0.92748321 0.5630603 ]
# [ 0.88537607 0.85550674 0.8643711 0.10000259 0.92410171]
# [ 0.07707875 0.54446853 0.06637628 0.75274004 0.32725236]]
#
# [[ 0.42021855 0.31693002 0.37445413 0.53950964 0.71708008]
# [ 0.96498739 0.99657426 0.16042028 0.57581363 0.76998479]
# [ 0.3587095 0.09490328 0.55956659 0.3640629 0.82835561]]] (2, 3, 5)
f.shape = (3,10)
print(f.shape) #(3, 10)第二种方法：不直接修改原数组（新旧数组会公用一个内存空间）
f = np.random.random((2,3,5))
ff = f.reshape((3,2,5))
print(f.shape) #(2, 3, 5)
print(ff.shape) #(3, 2, 5)4、元素级运算
回顾一下列表
a = [1,2,3]
b = ['aa','bb','cc']
print(a+b) #[1, 2, 3, 'aa', 'bb', 'cc']元素级运算：数组与数组之间的运算，要求同一个数据类型
a = np.array([1,2,3])
b = np.array([4,5,6])
print(a+b) #[5 7 9]
print(a-b) #[-3 -3 -3]
print(a*b) #[ 4 10 18]
print(a/b) #[ 0.25 0.4 0.5 ]
print(a**b) #[ 1 32 729]5、矩阵积
a = np.array([[1,2,3],[4,5,6]])
b = np.array([[3,4,5],[10,11,12]])
print(a.shape)
print(b.shape)
b.shape = (3,2)
print(a)
print(b)
print(np.dot(a,b))关于矩阵积的理解，推荐阮一峰老师的一篇文章http://www.ruanyifeng.com/blog/2015/09/matrix-multiplication.html