【编译原理】DFA自动机设计 算法&例题&代码实现
1.前言
设计DFA是编译原理中非常重要的一环,在词法分析中占有很重要的地位。一般而言,我们会先求正则表达式,然后根据正则表达式来求DFA。所以,在设计DFA之前,首先要确保你的正规文法正确。
简单的正规表达式可以直接求出DFA,但是稍微复杂的就困难了。一般而言DFA的设计需要经过三步,第一步,设计符合要求的ε-NFA;第二步,转化成DFA;第三步(如果没要求可省略),DFA的化简。
2.算法
2.1 ε-NFA设计
ε-NFA的定义:非确定性有限自动机。条件:1.自动机在某个状态下读取一个符号后转移的状态不唯一;2.符号含ε(空转换,表示不读入任何符号就转换状态)。
三种结构,分别是顺序、选择、循环,对应三个DFA模板:
1.顺序结构。
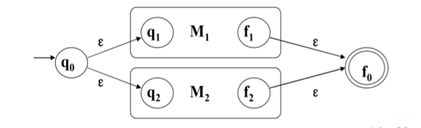
2.选择结构,M1、M2是被选择部分。
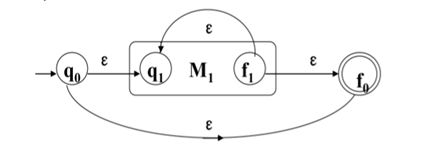
3.循环结构,M1是循环部分。
按照这三个模板去实现正则表达式,然后你就会发现有很多ε和很多“无用”状态,正是这些边和顶点的加入才使得ε-NFA的设计变得直观。实际上,上述给出的模板足够严谨却没有极致精简,在例题中我们将进一步精简表达。
2.2 ε-NFA转化DFA
DFA定义:确定性有限自动机。条件:有限状态机在读取一个符号后转移的状态唯一。
根据定义,DFA里不会出现空转移,也不会出现某状态读取相同符号后转移到不同的状态。
设原自动机ε-NFA={Pn,Vt,p1,pe,Q}.Pn为状态集合;Vt为转移符号xi集合(含ε);p1为开始状态;pe为终止状态;Q为转换规则。
设转换后的自动机DFA={Sn,Vt,s1,se,Q}.Sn为新状态集合;Vt为转移符号(不含ε);s1为新开始状态;Se为新终止状态集合;Q为新的转换规则。
1.S置为空。
2.从p1开始记录所有ε可以转移到的状态,记为s1={P0,Pi,...,Pj},s1∈Sn.
3.遍历Vt中所有非终结符。对于xi∈Vt(非终结符)记录下s1中状态能到达的状态集合,记为si={Pk,...Pj}。若si不为空,则si∈Sn。
4.对3中S增添的新状态重复3的操作。
5.反复执行3、4直到Sn不会增添新的元素。
ps:
对于新的DFA状态集合中元素si,如果含有原NFA的终止状态,则它是DFA的终止状态。
DFA的状态转移函数在3中求过了,如s1->as2。如果算法看起来难懂,没关系,下面我们有例子进行详解。
2.3 DFA的化简
DFA的化简主要是进一步删除具有相同功能的状态以及无用状态。
删除相同功能的状态的依据是状态是否可区分。直接观察DFA有时也能看出来哪些状态“具有相同的功能”。大多时候很难直接找到哪些状态是“有相同功能”的,于是我们从反面出发,研究哪些状态是具有不同的功能(可区分)。
设原自动机DFA={Pn,Vt,p1,pe,Q}.Pn为状态集合;Vt为转移符号xi集合(含ε);p1为开始状态;pe为终止状态;Q为转换规则。
定义状态的可区分:如果两个状态(p1,p2)分别属于Kn和Pn-Kn,那么这两个状态(p1,p2)可区分;如果两个状态(p1,p2)都属于Kn或者Pn-Kn,但是分别读取一个相同的符号x后转移到的两个新状态(p3,p4)分别处于Kn和Pn-Kn中,那么这两个状态仍然可区分。
根据可区分关系划分Pn的商集:
1.首先划分两个集合Kn与Pn-Kn,这两个集合的元素互相可区分。
2.对于剩下的、同处于相同集合的元素pi、pj执行:
每次尝试读取一个转移符号xi,观察转移后的状态pi'、pj'是否处于Kn与Pn-Kn两个状态集合。如果是,就判定pi,pj这两个状态可区分,否则对pi、pj尝试一个新的转移符号。如果所有的转移符号都尝试完,这pi、pj依旧不可区分,那么pi、pj不可区分,记为pi≡pj。
最终,记录下哪些状态对不可区分。
3.例题&代码
实现常数识别机:能够识别的数的形式包括整数、浮点数、科学计数。
首先确定符合要求的正规表达式,大概是d+ [. d+ [ (e | E) (+ | -) d+ ] ]
注意的一点是,这里我没有讨论识别负数,这是因为如果在常数识别这个任务识别了“-”,会给将来的语法分析带来麻烦。举例说:a-b,这个表达式在语法分析中是“《因式》《运算符》《因式》”的结构,也就是说结构合理。而如果过早识别了-,这个式子的结构就会变成“《因式》《因式》”,会被判错。所以,在常数识别的时候,不识别负数。
制作一个符合要求的DFA(下图-1表示无效输入,如空格等)。
然后根据DFA写一个简单的程序。
string judgeConst(char &ch, ifstream &infile)
{
string str = "";
int state = 0;
bool flag = false;
while (state != 7) //有限状态自动机,7为终止状态
{
switch (state)
{
case 0:
if ((ch >= '0' && ch <= '9') || ch == '-')
{
state = 1;
str += ch;
infile >> ch;
}
break;
case 1:
if (ch >= '0' && ch <= '9')
{
state = 1;
str += ch;
infile >> ch;
}
else if (ch == 'e' || ch == 'E')
{
state = 4;
str += ch;
infile >> ch;
}
else if (ch == '.')
{
state = 2;
str += ch;
infile >> ch;
}
else
{
state = 7;
flag = true;
}
break;
case 2:
if (ch >= '0' && ch <= '9')
{
state = 3;
str += ch;
infile >> ch;
}
break;
case 3:
if (ch == 'e' || ch == 'E')
{
state = 4;
str += ch;
infile >> ch;
}
else if (ch >= '0' && ch <= '9')
{
state = 3;
str += ch;
infile >> ch;
}
else
{
flag = true;
}
break;
case 4:
if (ch == '+' || ch == '-')
{
state = 5;
str += ch;
infile >> ch;
}
else if (ch >= '0' && ch <= '9')
{
state = 6;
str += ch;
infile >> ch;
}
break;
case 5:
if (ch >= '0' && ch <= '9')
{
state = 6;
str += ch;
infile >> ch;
}
break;
case 6:
if (ch >= '0' && ch <= '9')
{
state = 6;
str += ch;
infile >> ch;
}
if (ch < '0' || ch > '9')
{
state = 7;
}
break;
case 7:
flag = true;
break;
}
if (flag)
break;
}
return str;
}