牛客网编程题（1）

1. vivo第一题

在vivo产线上，每位职工随着对手机加工流程认识的熟悉和经验的增加，日产量也会不断攀升。
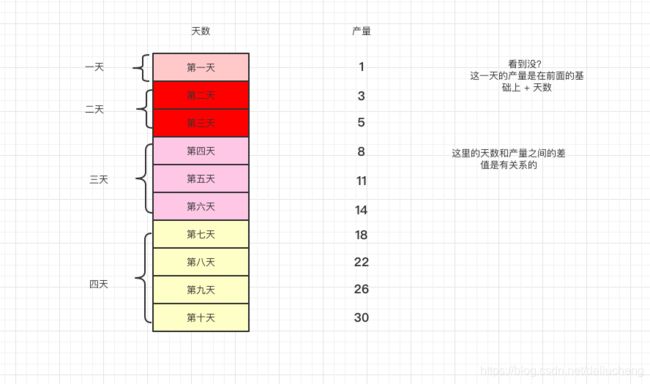
假设第一天量产1台，接下来2天(即第二、三天)每天量产2件，接下来3天(即第四、五、六天)每天量产3件 … …
以此类推，请编程计算出第n天总共可以量产的手机数量。

解析：

 public static void demo1() {
        int day = 5; //求第5天中可以量产的手机
        int[] result = new int[day + 1]; //定义 产量集合，下标为1代表第一天产量，下标为2代表第二天产量。以此类推
        int skip = 1;//定义步长。即就是每次增加的多少。
        int b = 0;//计数器，用来计数是1天还是2天还是三天。因为这个和skip有关 1天skip就是1，2天skip就是2
        for (int i = 1; i <= day; i++) {
            //今天的产量等于前一题+步长
            result[i] = result[i - 1] + skip;
            b++;//计数器++
            /*
             要注意：
                当b 和skip相等的时候 说明skip要➕一天
             */
            if (skip == b) {
                skip++;
                b = 0;//之后将skip规0，重新计数
            }
        }
        System.out.println(Arrays.toString(result));
    }

2. vivo第二题

现给定任意正整数 n，请寻找并输出最小的正整数 m（m>9），使得 m 的各位（个位、十位、百位 … …）之乘积等于n，若不存在则输出 -1。
例子：
输入： 100
输出： 455

思路：
- 先想如果是人来做应该怎么做？
1. 求100的因子。也就是 A * B = 100 ，从 9 开始除，最后找到是 除以 5 可能整除
2. 如果找到这个数（题目中也就是20）继续找这个数的因子，一直找到小于9
3. 然后就是按照个位，十位，百位。拼接起来就好
- 同样计算机也是这样
用递归做
1. 先是找好递归的出口，也就是 n < =9
2. 从9到1开始，找那个数能被这个数整除。
3. 如果能整除，将这个数继续递归
4. 递归的结果*10 + 被整除的数（1-9之间）返回

 /*
    现给定任意正整数 n，请寻找并输出最小的正整数 m（m>9），使得 m 的各位（个位、十位、百位 ... ...）之乘积等于n，若不存在则输出 -1。
     */
    public static int demo2(int number) {
        //输入36 -------》 输出49
        //因为要找最小的正整数  个位要从9开始除。如果能整除。得到的商继续递归运算 作为高位;

        if (number <= 9) {
            //递归出口
            return number;
        }

        for (int i = 9; i > 1; i--) {
            if (number % i == 0) {
                //能整除
                //高位继续递归
                int gaowei = number / i;
                int gaowei1 = demo2(gaowei);
                return gaowei1 * 10 + i;
            }
        }

        return -1;

    }

3. 华为2016 研发工程师（第一题）

有这样一道智力题：“某商店规定：三个空汽水瓶可以换一瓶汽水。小张手上有十个空汽水瓶，她最多可以换多少瓶汽水喝？”答案是5瓶，方法如下：先用9个空瓶子换3瓶汽水，喝掉3瓶满的，喝完以后4个空瓶子，用3个再换一瓶，喝掉这瓶满的，这时候剩2个空瓶子。然后你让老板先借给你一瓶汽水，喝掉这瓶满的，喝完以后用3个空瓶子换一瓶满的还给老板。如果小张手上有n个空汽水瓶，最多可以换多少瓶汽水喝？

思路：
有两种解题方式
- 数学归纳
经过写公式的推导，如果有n个空瓶子，就能换取n/2瓶汽水
- 递归求解
递归问题
3个瓶子换1瓶水+1个空瓶子，两个瓶子换1瓶水+0个空瓶子，1个瓶子换0瓶水。
f(1) = 0
f(2) = 1
f(3) = 1
f(4) = f(2)+1 //4个瓶子，其中3个可以换1瓶水+1个空瓶，所以是f(2)+1
f(5) = f(3)+1 //3个瓶子换1瓶水+1个空瓶，所以是f(3)+1
…
f(n) = f(n-2)+1
代码：

• 方法一：

import java.util.Scanner;
public class Main{
    public static void main(String[] args){
      Scanner scanner =   new Scanner(System.in);
      while (scanner.hasNext()){
         int n = scanner.nextInt();
          System.out.println(n/2);
      }
    }
}

• 方法二

import java.util.Scanner;
public class Main{
    public static void main(String[] args){
    demo6(10)
  }
		
	public static int demo6(int n) {
       if(n == 1){
            return 0;
        }
        if(n ==2 || n== 3){
            return 1;
        }
        return  demo6(n-2)+1;
	}
}

4. 华为2016 研发工程师（第二题）

明明想在学校中请一些同学一起做一项问卷调查，为了实验的客观性，他先用计算机生成了N个1到1000之间的随机整数（N≤1000），对于其中重复的数字，只保留一个，把其余相同的数去掉，不同的数对应着不同的学生的学号。然后再把这些数从小到大排序，按照排好的顺序去找同学做调查。请你协助明明完成“去重”与“排序”的工作(同一个测试用例里可能会有多组数据，希望大家能正确处理)。

思路：
这就是考察去重+排序

• 桶排序（空间换取时间）
• TreeSet（Treeset底层使用二叉排序树做的）
• 先去重复，后排序
  代码：
• 第一种

  Scanner scanner = new Scanner(System.in);
        int[] numbers = new int[1000];
        while (scanner.hasNextInt()) {
            for (int number : numbers) {
                number = 0;
            }//初始化。因为一次排序之后有残余
            int n = scanner.nextInt();//次数
            for (int i = 0; i < n; i++) {
                //按照桶排序
                int i1 = scanner.nextInt();
                numbers[i1] = i1;
            }
            for (int number : numbers) {
                if (number != 0) {
                    System.out.println(number);
                }
            }
        }

• 第二种

链接：https://www.nowcoder.com/questionTerminal/3245215fffb84b7b81285493eae92ff0
来源：牛客网

import java.util.*;
public class Main{
    public static void main(String[] args){
        Scanner scanner = new Scanner(System.in);
        TreeSet<Integer> numbers = new TreeSet<>();

        while (scanner.hasNextInt()) {
            numbers.clear();//初始化。因为一次排序之后有残余
            int n = scanner.nextInt();//次数

            for (int i = 0; i < n; i++) {
                
                int i1 = scanner.nextInt();
                numbers.add(i1);//在添加的时候已经拍好序
            }
            for (int number : numbers) {
                System.out.println(number);
            }
        }
    }
     
}

• 第三种（这就不写了）

5. 华为2016 研发工程师（第三题)

写出一个程序，接受一个十六进制的数，输出该数值的十进制表示。（多组同时输入 ）
输入：0xA
输出：10

思路
这里不是简单的一个parseInt就可以结束的，如果是超级超级大的数字，int或者long根本就放不下

• 创建一个arraylist，用来放置各个位置上对应的int数字
• 遍历输入的超级大的数字，将每个位置位置上对应的数变为int 存放上面的arraylist
• 定义一个bigDecimal 为sum
• 遍历arraylist 16进制变为10进制

 public static void demo6() {
 /*
 如果输入是substring十六进制 那么
 //        System.out.println("Long.parseLong: " + Long.parseLong(s, 16));//这个就会报错。因为超出可限制
 	
 */
        String substring = "0x1AFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF";
        String s = substring.substring(2); //去掉前面的0x。左开右闭
        //这里并不是简单的一个格式转换就好了,这里要考虑超大数字的转换
        ArrayList<Integer> integers = new ArrayList<>(); //存放各个位置对应的十进制
        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            int a = Integer.parseInt(c + "", 16);//变为十进制
            integers.add(a);
        }
        System.out.println(Arrays.toString(integers.toArray()));
        BigDecimal sum = new BigDecimal(0); //这个比较好
        int j = 0;
        for (int i = integers.size() - 1; i >= 0; i--) {

            long v = (long) (integers.get(i) * Math.pow(16, j++));
            sum = sum.add(new BigDecimal(v));
        }
        System.out.println("BigDecimal: " + sum);//这个就不会
//        System.out.println("Long.parseLong: " + Long.parseLong(s, 16));//这个就会报错。因为超出可限制

    }

6. 华为2016研发工程师编程题(第一题)

有一个数组a[N]顺序存放0~N-1，要求每隔两个数删掉一个数，到末尾时循环至开头继续进行，求最后一个被删掉的数的原始下标位置。以8个数(N=7)为例:｛0，1，2，3，4，5，6，7｝，0->1->2(删除)->3->4->5(删除)->6->7->0(删除),如此循环直到最后一个数被删除。

这个题的解法在我的数据结构面试题和常用算法（1）

7. 华为2016研发工程师编程题(第二题)

每组数据输入一个字符串，字符串最大长度为100，且只包含字母，不可能为空串，区分大小写。
输入：
abcqweracb
输出：
abcqwer

思路：
- 遍历 如果相等就让后一个变为; 输入的时候判断一哈就好
- 利用set去重

• 第一种

 public static void main(String[] args){
        Scanner scanner =    new Scanner(System.in);
        while (scanner.hasNext()){
            String next = scanner.next();
            char[] chars = next.toCharArray();
            
            for (int i = 0; i < chars.length; i++) {
                for (int j = i+1; j < chars.length; j++) {
                    if(chars[i]!=';' && chars[j] != ';'){
                        if(chars[i] == chars[j]){
                            chars[j] = ';';
                        }
                    }
                }
            }
            for (char aChar : chars) {
                if (aChar != ';'){
                    System.out.print(aChar);
                }
            }

        }
    }

• 第二种

import java.util.HashSet;
import java.util.Scanner;
import java.util.Set;
public class Main{
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        while(in.hasNext()){
            char[] c = in.next().toCharArray();
            StringBuffer sb = new StringBuffer();
            Set<Character> set = new HashSet<Character>();
            for(int i = 0;i<c.length;i++){
                if(set.add(c[i]))
                    sb.append(c[i]);
            }
            System.out.println(sb.toString());
        }
    }
}

7. 华为2016研发工程师编程题(第三题)

数独是一个我们都非常熟悉的经典游戏，运用计算机我们可以很快地解开数独难题，现在有一些简单的数独题目，请编写一个程序求解。

这个题我还没有怎么懂。后续更新

import java.util.*;
public class Main{   
    public static void main(String[] args){
        Scanner sc=new Scanner(System.in);
        while(sc.hasNext()){
            int[][] data=new int[9][9];
            ArrayList<HashSet<Integer>> row=new ArrayList<HashSet<Integer>>();
            ArrayList<HashSet<Integer>> col=new ArrayList<HashSet<Integer>>();
            ArrayList<HashSet<Integer>> squ=new ArrayList<HashSet<Integer>>();
             
            for(int i=0;i<9;i++){
                row.add(new HashSet<Integer>());
                col.add(new HashSet<Integer>());
                squ.add(new HashSet<Integer>());
            }
             
            for(int i=0;i<9;i++){
                for(int j=0;j<9;j++){
                    data[i][j]=sc.nextInt();
                    if(data[i][j]!=0){
                        row.get(i).add(data[i][j]);
                        col.get(j).add(data[i][j]);
                        squ.get(i/3*3+j/3).add(data[i][j]);
                    }
                }
            }
             
            dfs(data,row,col,squ,0);
 
            for(int i=0;i<9;i++){
                for(int j=0;j<9;j++){
                    if(j!=8)
                        System.out.print(data[i][j]+" ");
                    else
                        System.out.println(data[i][j]);
                }
            }
        }
        sc.close();
    }
     
     
    public static boolean dfs(int[][] data,ArrayList<HashSet<Integer>> row,ArrayList<HashSet<Integer>> col,ArrayList<HashSet<Integer>> squ,int index){
        if(index==81)
            return true;       
        int m=index/9;
        int n=index%9;
        int k=m/3*3+n/3;
         
        if(data[m][n]!=0){
            return dfs(data,row,col,squ,index+1);
        }
        else{
            for(int i=1;i<=9;i++){
                if(!row.get(m).contains(i) && !col.get(n).contains(i) && !squ.get(k).contains(i)){
                    data[m][n]=i;
                    row.get(m).add(i);
                    col.get(n).add(i);
                    squ.get(k).add(i);
                    if(dfs(data,row,col,squ,index+1))
                        return true;
                    data[m][n]=0;
                    row.get(m).remove(i);
                    col.get(n).remove(i);
                    squ.get(k).remove(i);
                }
            }
            return false;
        }
    }
}