【ECCV2020】 Context-Gated Convolution

论文：https://arxiv.org/abs/1910.05577

代码：https://github.com/XudongLinthu/context-gated-convolution

这是来自哥伦比亚大学和腾讯 AI lab 的工作，也是一种即插即用的模块。

论文的动机为：Neurons do change their function according to contexts and task. 但是传统的CNN并不具有这样的性质。当前也出现了一些方法，作者命名为global feature interaction，如下图所示。这些方法（non-local, SENet, CBAM等）考虑到既然卷积层不具有这样的能力，在卷积之前通过 feature interatction 的方式操作。这些方法仍没有办法对卷积核建模做到“changing the structure of correlations over neuronal ensembles”。

作者提出的Context-Gated Convolution，把卷积层当做一个“自适应的处理器”，可以根据图像中的语义信息来调整卷积核的权重。

这个方法实现起来并不容易，因为对于输入feature map 的尺寸为 \((c, h , w)\)， 输出 feature map 的尺寸为 \((o, h, w)\)，这样，卷积参数量就是 \(o\times c \times k\times k\)。所以，必须把卷积分解为两个：\(o\times k\times k\)和 \(c \times k \times k\) 。

这样来看，还是比较复杂，因此，又进一步借鉴了 depth-wise separable 可分离卷积的思想。

方法的总体架构如下图所示，包含三个关键模块：context encoding module, channel interacting module, 和 gate decoding module。

1、Context encoding module

对于输入为 \(chw\) 的特征，使用pooling降维成 \(ch'w'\)，转后把 \(h\times w\)这个维度转化成一维向量 \(d\)。 论文里提到，如果 \(d\) 没有定义，就使用 \((k_1\times k_2)/2\)。经过这个模块处理，作出的特征为 \(c\times d\)。因为下一步要输出到两个模块，因此，使用了两个独立的BN层。代码如下：

# the context encoding module
self.ce = nn.Linear(ws*ws, num_lat, False)            
self.ce_bn = nn.BatchNorm1d(in_channels)
self.ci_bn2 = nn.BatchNorm1d(in_channels)
# activation function is relu
self.act = nn.ReLU(inplace=True)

2、 Channel Interaction module

这个模块把输入\(c\times d\)的特征转化为 \(o\times d\)的特征。为了保证高效性，这里使用了 grouped FC，代码如下：

# the number of groups in the channel interacting module
if in_channels // 16:
   self.g = 16
else:
  self.g = in_channels
# the channel interacting module    
self.ci = nn.Linear(self.g, out_channels // (in_channels // self.g), bias=False)
self.ci_bn = nn.BatchNorm1d(out_channels)

3、Gate decoding module

这个模块接收两个输入，对于\(c\times d\)的输入，使用FC转化成 \(c\times k_1 \times k_2\)的特征； 对于 \(o\times d\) 输入，使用FC转化成 \(o\times k_1 \times k_2\) 的特征。然后，两组特征分别沿两个方向复制，得到 \(o\times c \times k_1 \times k_2\) 的特征，然后加一个 sigmoid 函数，实现 gate 操作。代码如下：

# produce gate
out = self.sig(out.view(b, 1, c, self.ks, self.ks) +    oc.view(b, self.oc, 1, self.ks, self.ks))

最后，把得到的结果，逐元素点乘的方式与 卷积核 融合。

由于在关键的步骤使用了 Grouped FC，所以计算量并没有显著增加，但是因为给卷积核上每个点添加了权重 （注意力机制），性能得到了提升。具体可以参考论文在 ImageNet 和 CIFAR10 上的实验。

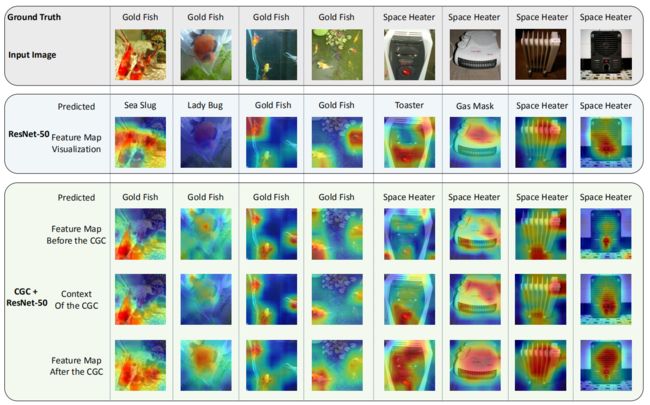
论文中有一个比较有趣的实验是 feature map 的可视化。在第一列里，可以看到 ResNet 对于金鱼的捕获不是特别准确，但是 CGC 方法就可以准确的捕获金鱼区域。

一些想法

这是我第一次看到给卷积核逐点分配权重，还是比较有意思。Gate decoding module 里，把 \(c\times k_1 \times k_2\)的特征和 \(o\times k_1 \times k_2\) 的特征，分别沿两个方向复制，得到 \(o\times c \times k_1 \times k_2\) 的特征，让我忽然想到了 程明明组的 strip pooling 。不过， strip pooling 仍然是给 feature map 分配权重，这个工作是给卷积核分配权重。