深入浅出理解Dilated Convolution(空洞卷积,膨胀卷积)
温故而知新,可以为师矣!
一、参考资料
github仓库:Multi-Scale Context Aggregation by Dilated Convolutions
图片素材来源:Convolution arithmetic
理解Dilation convolution
Dilated Convolution —— 空洞卷积(膨胀卷积)
膨胀卷积学习笔记
二、空洞卷积(Dilated Convolution)相关介绍
1. 引言
1.1 增大感受野
用CNN进行图像处理时,通常需要经过多次卷积和pooling操作,pooling操作可以减少图像的尺寸,再使用卷积核可以增大感受野;多个卷积核堆叠也可以增大感受野。但是,在图像分割任务中,例如FCN[3],由于图像分割预测是 pixel-wise 的输出,所以要将pooling操作后较小尺寸的 feature map 通过 upsampling 的方法(如Conv2DTranspose转置卷积)恢复到原始图像尺寸,再进行预测。如下图所示:

因此,图像分割FCN中有两个关键,一个是pooling操作减小图像尺寸增大感受野,另一个是 upsampling 扩大图像尺寸。在先减小再增大尺寸的过程中,导致一些细节信息的损失。那么能不能设计一种新的操作,不通过pooling操作也能有较大的感受野看到更多的信息呢?答案就是Dilated Convolution。
1.2 up-sampling 和 pooling layer 存在的问题
图像分割任务中,较为著名的是 up-sampling 和 pooling layer 的设计,但这些设计存在一些致命性的缺陷,主要问题有:
- 参数不可学习:Up-sampling / pooling layer (e.g. bilinear interpolation) is deterministic。
- 内部数据结构丢失,空间层级化信息丢失。
- 小物体信息无法重建:如果一个物体占4x4的像素,则经过4次pooling操作之后,物体的信息就无法重构了。换句话说,假设有4个pooling layer,则任何小于 2 4 = 16 p i x e l 2^4=16 pixel 24=16pixel 的物体信息将理论上无法重建。
- pooling操作是不可逆转的,通过对
feature map进行upsampling还原图像尺寸时丢失信息。
在这样问题的存在下,图像分割问题一直处在瓶颈期无法再明显提高精度, 而 Dilated Convolution 的设计很好的避免了这些问题。
2. Dilated Convolution的概念
Dilated Convolution,中文叫做空洞卷积或者膨胀卷积,是一种通过增加卷积核(kernel)元素间距(padding 0)使得感受野增加的一种卷积方式。
3. dilation rate
Dilated Convolution是在标准卷积Convolution map的基础上注入空洞,以此来增加感受野(reception field)。因此,Dilated Convolution在标准卷积的基础上多了一个超参数(hyper-parameter)称之为膨胀率(dilation rate),表示卷积核的间隔。 dilation rate 控制卷积时的padding 以及 dilation rate,通过不同的填充以及与膨胀,可以获取不同尺度的感受野,提取多尺度的信息。
如下图所示,Dilated Convolution与标准卷积采用的都是3x3卷积核,标准卷积的 dilation rate 为1,Dilated Convolution 的 dilation rate 为2。

4. Dilated Convolution 的作用
Dilated Convolution 代替了传统的 max-pooling 和 strided convolution,能够增大感受野,并保持 feature map 的尺寸和原始图片大小。
Dilated Convolution 的好处是不做pooling损失信息的情况下,加大了感受野,让每个卷积输出都包含较大范围的信息。在图像需要全局信息或者语音文本需要较长的sequence信息依赖的问题中,都能很好的应用 Dilated Convolution,比如图像分割[3]、语音合成WaveNet[2]、机器翻译ByteNet[1]中。
5. Conv2DTranspose与Dilated Convolution的区别
Conv2DTranspose 其中的一个用途是做upsampling,即增大图像尺寸。而 Dilated Convolution 并不是做upsampling,而是增大感受野。
Dilated Convolution 不是在像素之间padding空白的像素,而是在已有的像素上,skip掉一些像素,或者输入不变,对conv的kernel参数中插一些0的weight,达到一次卷积看到的空间范围变大的目的。
当然将标准卷积的 stride 步长设为大于1,也会达到增大感受野的效果,但是 stride 大于1就会导致 downsampling,图像尺寸变小。
6. Dilated Convolution存在的问题
-
栅格效应(The Gridding Effect)
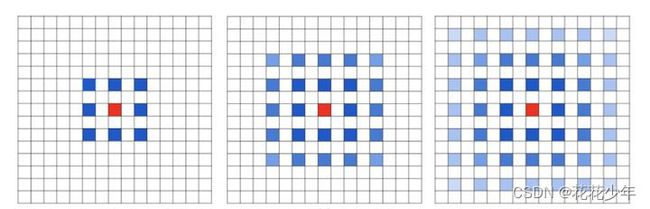
如果我们叠加多个相同的
Dilated Convolution,会发现感受野中有很多像素没有利用上,出现大量空洞。此时,会丢失数据之间的连续性和完整性,不利于学习。如下图所示,展示了连续进行3次相同Dilated Convolution的效果(卷积核大小为3x3,dilation rate=2)。
-
Long-ranged information might be not relevant
Dilated Convolution的设计是为了获取long-range-information,有些长距离信息和当前点是完全不相关的,会影响数据的一致性。并且,仅采用大的 dilation rate 的信息,可能对大物体有较好的分割效果,而对小物体可能有弊无利。如何同时处理好大物体和小物体的关系,则是设计好Dilated Convolution网络的关键。
7. 混合膨胀卷积 (HDC)
混合膨胀卷积 (Hybrid Dilated Convolution,HDC)。
-
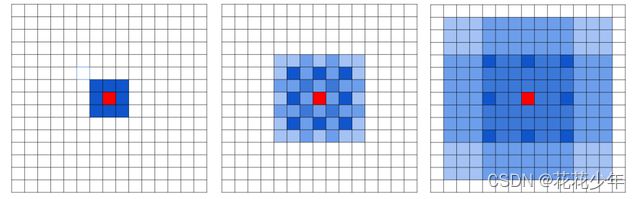
不同的卷积层使用不同的
dilation rate。对于一组Dilated Convolution,设置不同的dilation rate,且dilation rate逐渐增大。例如,3个卷积核可以分别设置dilation rate为 [1, 2, 4]。这样最后一层有比较大的感受野,同时不会丢失大量的局部信息。如下图所示:
-
使多个
Dilated Convolution后的感受野内不存在空洞。假设有n个膨胀卷积核,dilation rate分别是 [r1, r2,…, rn]。如果 [r1, r2,…, rn] 能使下式成立,则说明感受野不会存在空洞。

上式中的 M i M_i Mi 指的是第 i 层可以使用的最大的dilation rate,K是卷积核尺寸。
三、相关经验
1. GrabAR
GrabAR: Occlusion-aware Grabbing Virtual Objects in AR
附件:Supplementary material, A. GrabAR-Net architecture details
四、参考文献
[1] Kalchbrenner N, Espeholt L, Simonyan K, et al. Neural machine translation in linear time[J]. arxiv preprint arxiv:1610.10099, 2016.
[2] Oord A, Dieleman S, Zen H, et al. Wavenet: A generative model for raw audio[J]. arxiv preprint arxiv:1609.03499, 2016.
[3] Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2015: 3431-3440.
[4] Yu F, Koltun V. Multi-scale context aggregation by dilated convolutions[J]. arXiv preprint arXiv:1511.07122, 2015.