Transformer变体（Star-Transformer，Transformer-XL）

Star-Transformer
来自NAACL 2019的论文。
问题：

• Transformer的自注意力机制每次都要计算所有词之间的注意力，其计算复杂度为输入长度的平方，结构很重
• 在语言序列中相邻的词往往本身就会有较强的相关性，似乎本来就不需要计算所有词之间

解决：
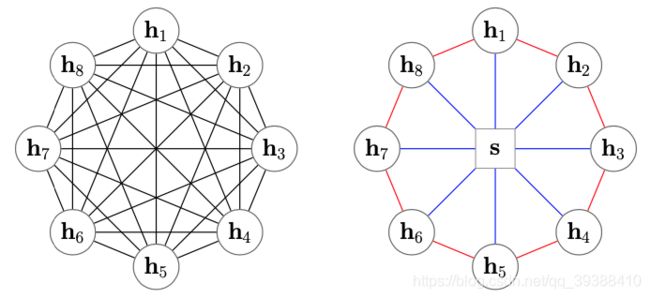
Star-Transformer用星型拓扑结构代替了全连通结构如上图左边是Transformer，而右边是Star-Transformer。在右边的图中，所有序列中直接相邻的词可以直接相互作用，而非直接相邻的元素则通过中心节点实现间接得信息传递，因此，复杂性从二次降低到线性，同时保留捕获局部成分和长期依赖关系的能力。

• Radical connections， 捕捉非局部信息。即每两个不相邻的卫星节点都是两跳邻居，可以通过两步更新接收非局部信息。
• Ring connections， 捕捉局部信息。 由于文本输入是一个序列，相邻词相连以捕捉局部成分之间的关系。值得注意的是它第一个节点和最后一个节点也连接起来，形成环形连接。

具体实现算法如下：

• 在初始化阶段，卫星节点（周围的词节点）的初始值为各自相应的词向量 $e_1....e_n$，而中心节点（集成节点）的初始值为所有词节点词向量的平均值 $average(e_1....e_n)$。
• 更新卫星节点。对于某卫星节点 $i$，先得到它的上下文信息 $C_i^t$，它由相邻节点$h_{i-1}、h_{i+1}$，中心节点$s$，和这个节点对应的token词嵌入$e^i$组成。然后多头注意力更新特征，最后使用层归一化。
• 更新中心节点（relay node）。中心节点与上一时刻和所有卫星信息的交互，所以同样是多头注意力$MultiAtt(s^{t-1},s^{t-1})$，H是可学习的位置编码（它在所有时刻都是一样的）。
• 交替更新T步，over。

paper：https://arxiv.org/abs/1902.09113
code：https://github.com/fastnlp/fastNLP

Transformer-XL
Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context，ACL 2019
问题：

• Transformer可以学习到输入文本的长距离依赖关系和全局特性，但是！ 需要事先设定输入长度，这导致了其对于长程关系的捕捉有了一定限制。
• 出于效率的考虑，需要对输入的整个文档进行分割（固定的），那么每个序列的计算相互独立，所以只能够学习到同个序列内的语义联系，整体上看，这将会导致文档语意上下文的碎片化(context fragmentation)。

那么如何学习更长语义联系？

segment-level Recurrence
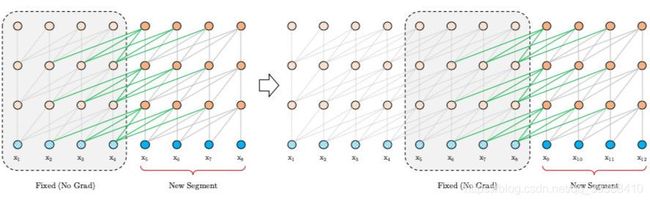
segment-level循环机制。如上图左边为原始 Transformer，右边为 Transformer-XL，Transformer-XL 模型的计算当中加入绿色连线，使得当层的输入取决于本序列和上一个序列前一层的输出。这样每个序列计算后的隐状态会参与到下一个序列的计算当中，使得模型能够学习到跨序列的语义联系。（看动图可能更好理解）

$h_r^n$是第$r$个segment的第n层隐向量，那么第r+1个的第n层的隐向量的计算，就是上面这套公式。

• 其中SG是是stop-gradient，不再对$s_t$的隐向量做反向传播（这样虽然在计算中运用了前一个序列的计算结果，但是在反向传播中并不对其进行梯度的更新，毕竟前一个梯度肯定不受影响）。
• ${\overline{h}}_{r+1}^{n-1}$是对两个隐向量序列沿长度L方向的拼接 。3个W分别对应query，key和value的转化矩阵，需要注意的是！k和v的W用的是$h_{r+1}^{n-1}$，而q是用的${\overline{h}}_{r+1}^{n-1}$，即kv是用的拼接之后的h，而q用的是原始序列的信息。感觉可以理解为以原始序列查拼接序列，这样可以得到一些前一个序列的部分信息以实现跨语义。
• 最后的公式是标准的Transformer。

还有一点设计是，在评估预测模型的时候它是会连续计算前L个长度的隐向量的（训练的时候只有前一个，缓存在内存中）。即每一个位置的隐向量，除了自己的位置，都跟下一层中前(L-1)个位置的token存在依赖关系，而且每往下走一层，依赖关系长度会增加(L-1)，这样能使跨语义更加的深入。

只看看XL多头注意力的forward的不同地方吧

def forward(self, w, r, r_w_bias, r_r_bias, attn_mask=None, mems=None):
 			#w是上一层的输出，r是相对位置嵌入（在下一节），r_w_bias是u，r_r_bias是v向量
	        qlen, rlen, bsz = w.size(0), r.size(0), w.size(1)
	
	        if mems is not None: #mems就是前一些序列的向量，不为空
	            cat = torch.cat([mems, w], 0) #就拼起来
	            if self.pre_lnorm: #如果有正则化
	                w_heads = self.qkv_net(self.layer_norm(cat)) #这个net是nn.Linear，即qkv的变换矩阵W参数
	            else:
	                w_heads = self.qkv_net(cat)#没有正则就直接投影一下
	            r_head_k = self.r_net(r)#也是nn.Linear
	
	            w_head_q, w_head_k, w_head_v = torch.chunk(w_heads, 3, dim=-1) #复制3份
	            w_head_q = w_head_q[-qlen:] #q的W不要拼接的mems
	        else:#没有mems，就正常的计算
	            if self.pre_lnorm:
	                w_heads = self.qkv_net(self.layer_norm(w))
	            else:
	                w_heads = self.qkv_net(w)
	            r_head_k = self.r_net(r)
	
	            w_head_q, w_head_k, w_head_v = torch.chunk(w_heads, 3, dim=-1)
	
	        klen = w_head_k.size(0)
		    #qlen是序列长度，bsz是batch size，n_head是注意力头数，d_head是每个头的隐层维度
	        w_head_q = w_head_q.view(qlen, bsz, self.n_head, self.d_head)           # qlen x bsz x n_head x d_head
	        w_head_k = w_head_k.view(klen, bsz, self.n_head, self.d_head)           # qlen x bsz x n_head x d_head
	        w_head_v = w_head_v.view(klen, bsz, self.n_head, self.d_head)           # qlen x bsz x n_head x d_head
	
	        r_head_k = r_head_k.view(rlen, self.n_head, self.d_head)                # qlen x n_head x d_head
	
	        ####计算注意力的四个部分
	        #AC是指相对位置的公式里的a和c两个部分，相对位置在下一节做笔记
	        rw_head_q = w_head_q + r_w_bias                                         # qlen x bsz x n_head x d_head
	        
	        #爱因斯坦简记法求和sum，统一的方式表示各种各样的张量运算
	        AC = torch.einsum('ibnd,jbnd->ijbn', (rw_head_q, w_head_k))             # qlen x klen x bsz x n_head
	
	        #BD是指相对位置的公式里的b和d两个部分
	        rr_head_q = w_head_q + r_r_bias
	       
	        BD = torch.einsum('ibnd,jnd->ijbn', (rr_head_q, r_head_k))              # qlen x klen x bsz x n_head
	        BD = self._rel_shift(BD)
	
	        # [qlen x klen x bsz x n_head]
	        attn_score = AC + BD #最后的结果
	        attn_score.mul_(self.scale)#进行放缩

Relative Position Encodings
相对位置编码。原始 Transformer 采用了正弦/余弦函数来编码绝对位置信息。然而因为Transformer-XL 会有多个句子，所以还是绝对位置，那么两个句子的相同位置是同样的编码，比如 [0, 1, 2, 3] 在两个句子concat之后就变成了[0, 1, 2, 3, 0, 1, 2, 3]，句子不连续，而且每次拼的句子会不一样，也不能找到适合的绝对位置编码。所以这里使用相对位置编码。

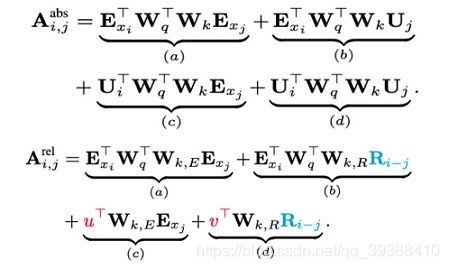
上图是原始Transformer和Transformer-XL的比较，其中 E 表示词的 Embedding，而 U 表示绝对位置编码。这大一堆看起来奇奇怪怪，实际上Transformer的注意力计算是$(E_{x_i}+U_i)W_q{W}_k(E_{x_j}+U_j)$的分解，即先编码Q（当前词 i）和K（其他的词 j）然后算内积，位置编码是直接add在词嵌入上面的。

而Transformer-XL的改变是：

• 把 j 的绝对位置U换成了相对位置R，该相对位置表示也是一个正弦函数表示（i和j的相对位置向量，j是之前的序列，所以相减一定是正数）。R不是通过学习得到的，好处是预测时，可以使用比训练距离更长的位置向量。
• 使用两个可学习参数 u 和 v 替代了中的 query i 的位置映射。这里是由于每次计算query向量是固定的，不需要编码。
• 每一层的Attention计算都要相对位置编码。Transformer里面只有input的时候会加，而XL需要每层。

细细思考，这attention的四个部分各有玄机：

• a. 基于内容的“寻址”，即没有添加原始位置编码的原始向量，$E_{x_i}$查$E_{x_i}$。
• b. 基于内容的位置偏置，即相对于当前内容的位置偏差，$E_{x_i}$查$R_{i-j}$。
• c. 全局的内容偏置，用于衡量key的重要性，query固定查$E_{x_j}$。
• d. 全局的位置偏置，根据query和key之间的距离调整重要性，query固定查$R_{i-j}$。

相对位置编码的代码为：

class PositionalEmbedding(nn.Module):
    def __init__(self, demb):
        super(PositionalEmbedding, self).__init__()
        self.demb = demb #编码维度
        inv_freq = 1 / (10000 ** (torch.arange(0.0, demb, 2.0) / demb)) #间隔频率

    def forward(self, pos_seq):
        sinusoid_inp = torch.ger(pos_seq, self.inv_freq) #序列的位置向量 operation 间隔
        pos_emb = torch.cat([sinusoid_inp.sin(), sinusoid_inp.cos()], dim=-1) #正弦余弦
        return pos_emb[:,None,:] #直接返回R，非学习矩阵R

简单把编码维度设置为10，查询向量也是10个，存储之前的序列也是10，有以下结果：

>>> import torch
>>> inv_freq = 1 / (10000 ** (torch.arange(0.0, 10, 2.0) / 10))
>>> inv_freq
tensor([1.0000e+00, 1.5849e-01, 2.5119e-02, 3.9811e-03, 6.3096e-04])
>>> pos_seq=torch.arange(20-1, -1, -1.0) #qlen+mlen，即10+10的维度然后逆序
>>> pos_seq
tensor([19., 18., 17., 16., 15., 14., 13., 12., 11., 10.,  9.,  8.,  7.,  6.,
         5.,  4.,  3.,  2.,  1.,  0.])
>>> sinusoid_inp = torch.ger(pos_seq,inv_freq)
>>> sinusoid_inp
tensor([[1.9000e+01, 3.0113e+00, 4.7726e-01, 7.5640e-02, 1.1988e-02],
        [1.8000e+01, 2.8528e+00, 4.5214e-01, 7.1659e-02, 1.1357e-02],
        [1.7000e+01, 2.6943e+00, 4.2702e-01, 6.7678e-02, 1.0726e-02],
        [1.6000e+01, 2.5358e+00, 4.0190e-01, 6.3697e-02, 1.0095e-02],
        [1.5000e+01, 2.3773e+00, 3.7678e-01, 5.9716e-02, 9.4644e-03],
        [1.4000e+01, 2.2189e+00, 3.5166e-01, 5.5735e-02, 8.8334e-03],
        [1.3000e+01, 2.0604e+00, 3.2655e-01, 5.1754e-02, 8.2024e-03],
        [1.2000e+01, 1.9019e+00, 3.0143e-01, 4.7773e-02, 7.5715e-03],
        [1.1000e+01, 1.7434e+00, 2.7631e-01, 4.3792e-02, 6.9405e-03],
        [1.0000e+01, 1.5849e+00, 2.5119e-01, 3.9811e-02, 6.3096e-03],
        [9.0000e+00, 1.4264e+00, 2.2607e-01, 3.5830e-02, 5.6786e-03],
        [8.0000e+00, 1.2679e+00, 2.0095e-01, 3.1849e-02, 5.0477e-03],
        [7.0000e+00, 1.1094e+00, 1.7583e-01, 2.7867e-02, 4.4167e-03],
        [6.0000e+00, 9.5094e-01, 1.5071e-01, 2.3886e-02, 3.7857e-03],
        [5.0000e+00, 7.9245e-01, 1.2559e-01, 1.9905e-02, 3.1548e-03],
        [4.0000e+00, 6.3396e-01, 1.0048e-01, 1.5924e-02, 2.5238e-03],
        [3.0000e+00, 4.7547e-01, 7.5357e-02, 1.1943e-02, 1.8929e-03],
        [2.0000e+00, 3.1698e-01, 5.0238e-02, 7.9621e-03, 1.2619e-03],
        [1.0000e+00, 1.5849e-01, 2.5119e-02, 3.9811e-03, 6.3096e-04],
        [0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00]])
>>> sinusoid_inp.sin()
tensor([[ 1.4988e-01,  1.2993e-01,  4.5935e-01,  7.5568e-02,  1.1988e-02],
        [-7.5099e-01,  2.8479e-01,  4.3689e-01,  7.1598e-02,  1.1357e-02],
        [-9.6140e-01,  4.3251e-01,  4.1416e-01,  6.7627e-02,  1.0726e-02],
        [-2.8790e-01,  5.6939e-01,  3.9117e-01,  6.3654e-02,  1.0095e-02],
        [ 6.5029e-01,  6.9200e-01,  3.6793e-01,  5.9681e-02,  9.4642e-03],
        [ 9.9061e-01,  7.9726e-01,  3.4446e-01,  5.5706e-02,  8.8333e-03],
        [ 4.2017e-01,  8.8254e-01,  3.2077e-01,  5.1731e-02,  8.2024e-03],
        [-5.3657e-01,  9.4569e-01,  2.9688e-01,  4.7755e-02,  7.5714e-03],
        [-9.9999e-01,  9.8514e-01,  2.7281e-01,  4.3778e-02,  6.9405e-03],
        [-5.4402e-01,  9.9990e-01,  2.4856e-01,  3.9800e-02,  6.3095e-03],
        [ 4.1212e-01,  9.8959e-01,  2.2415e-01,  3.5822e-02,  5.6786e-03],
        [ 9.8936e-01,  9.5448e-01,  1.9960e-01,  3.1843e-02,  5.0476e-03],
        [ 6.5699e-01,  8.9544e-01,  1.7493e-01,  2.7864e-02,  4.4167e-03],
        [-2.7942e-01,  8.1396e-01,  1.5014e-01,  2.3884e-02,  3.7857e-03],
        [-9.5892e-01,  7.1207e-01,  1.2526e-01,  1.9904e-02,  3.1548e-03],
        [-7.5680e-01,  5.9234e-01,  1.0031e-01,  1.5924e-02,  2.5238e-03],
        [ 1.4112e-01,  4.5775e-01,  7.5285e-02,  1.1943e-02,  1.8929e-03],
        [ 9.0930e-01,  3.1170e-01,  5.0217e-02,  7.9621e-03,  1.2619e-03],
        [ 8.4147e-01,  1.5783e-01,  2.5116e-02,  3.9811e-03,  6.3096e-04],
        [ 0.0000e+00,  0.0000e+00,  0.0000e+00,  0.0000e+00,  0.0000e+00]])

使用Transformer-XL的预训练模型经典的就是XLNet啦，可以更好的处理较长的文本。

作者的论文和代码开源：
paper：https://arxiv.org/abs/1901.02860
code：https://github.com/kimiyoung/transformer-xl