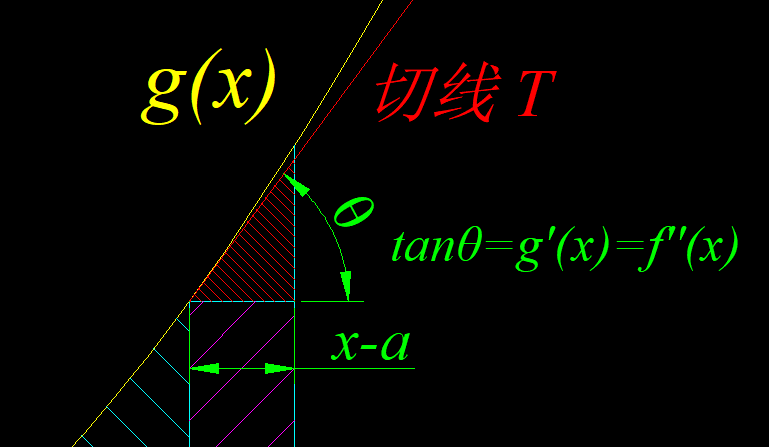来看看比尔盖茨当年写的BASIC解释器源代码吧，你就知道泰勒级数有什么用了...

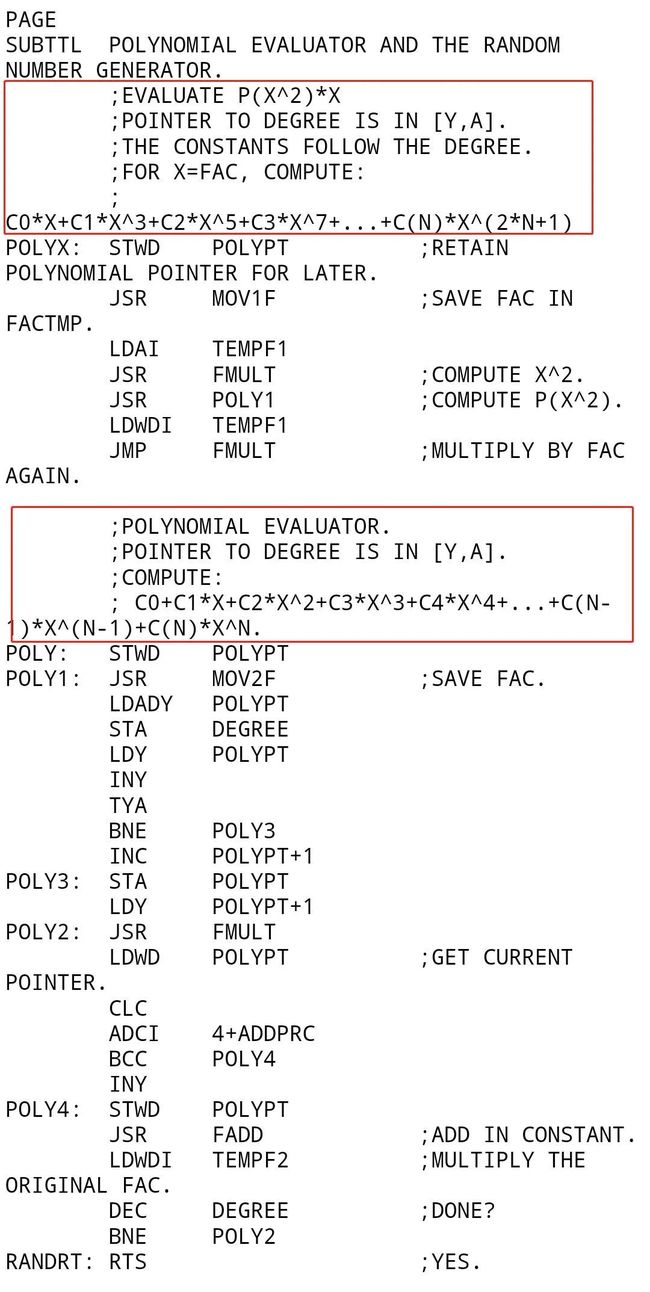
几年前当我刚上大学那会，我曾经问过我一位学计算机同学的一个问题：计算机是如何计算诸如   或者   这种运算的？当初这个问题曾经困扰了我好长时间，这个问题并非是我当年在微积分课堂上解决的，而是直到我后来接触编程后才彻底恍然大悟。那么计算机究竟是如何计算这类运算呢？带着这个问题，我们先来看看当年比尔盖茨在上世纪七十年代写的BASIC解释器的部分源代码吧。

代码部分内容：

完整源代码链接

https://www.pagetable.com/docs/M6502.MAC.txt

盖茨的这些代码公布于两年前，当时在网上引起了不小风波。

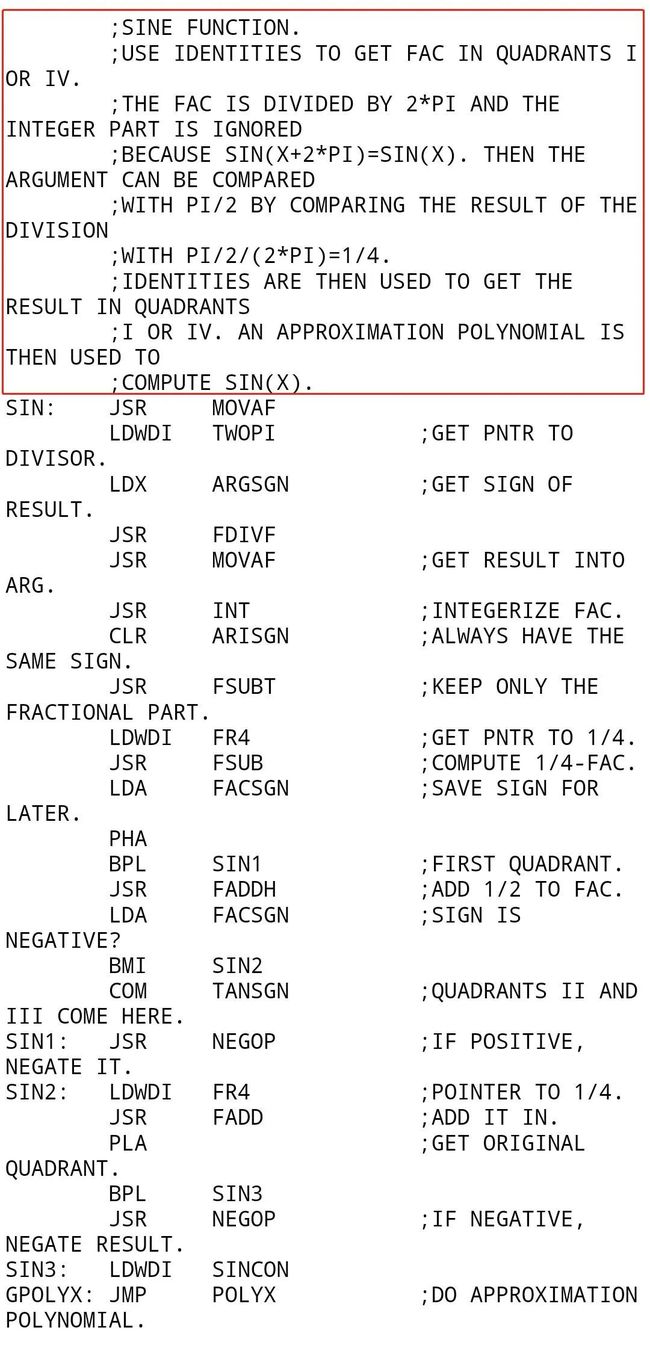
对于这段汇编代码，即便你看不懂，但你仅从注释部分（我标注的红框内）也能猜出是计算正弦sin函数的方法。如果你汇编基础好的话，仔细研究，发现盖茨用的正是泰勒公式来逼近这个   函数的。也即：  暂且不说编程逻辑、算法效率方面如何，单是从注释习惯方面已经足够秒杀现在大部分的软件从业人员了。如果非要说算法的话，这个算法已经是被盖茨压榨到了极限，开始部分就先判断象限，再将角度进行区间的转化。

要知道，在比尔盖茨那个年代，市场上还没有软件工程这个概念。。。而盖茨这部分代码却包含了完整的注释，极简的算法。想想多恐怖。

嗯，扯远了，今天我们不聊汇编，主要聊一聊盖茨使用的这个算法，也就是泰勒级数。

盖茨使用的这个算法，延续到了现代计算器上面。

无独有偶，前不久微软在GitHub上面开源了其Windows上面自带计算器应用的C++源代码（计算引擎部分用C++，UI部分使用C#）

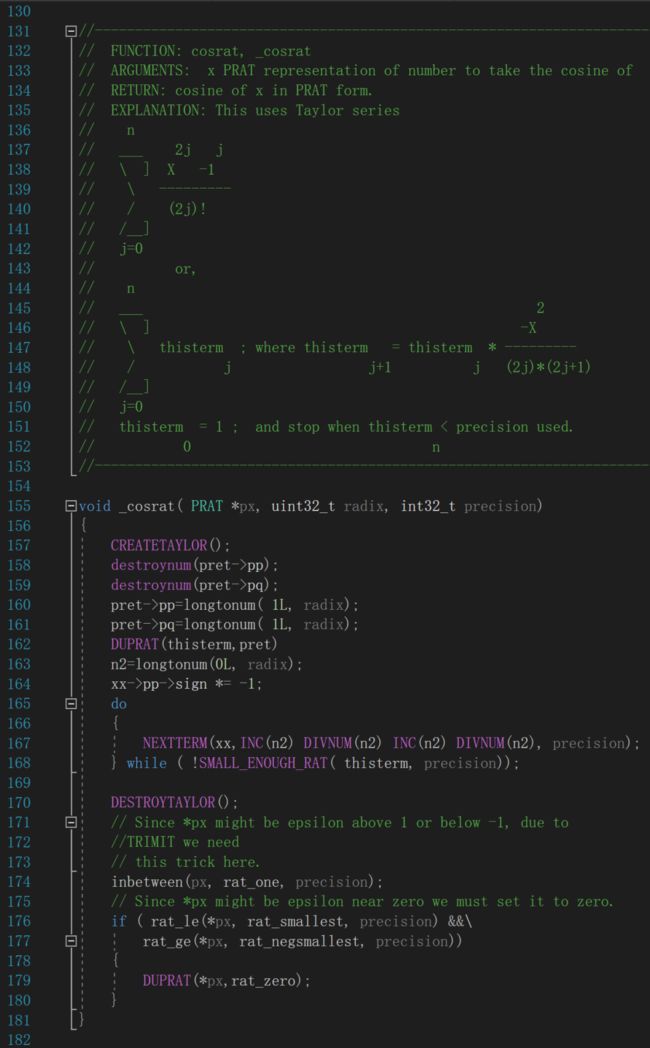
部分C++源代码:

完整代码且看

https://github.com/Microsoft/calculator

对于上面的代码，得益于微软工程师完美的代码注释，即便你没有编程基础的话，你依然能够从注释里面看出本行代码的大致意思，没错，这段代码就是求余弦   的函数。再仔细观察注释部分，你能发现，哈哈，你能发现微软的工程师挺皮的，居然把   函数的泰勒展开给画出来了。我甚至怀疑微软的工程师是不是继承了盖茨的编码注释风格，居然如此详细。

如果那两段汇编你可能看不懂的话，那么上面这段C++代码你肯定能有所领悟。其实这段代码跟上面那段汇编有同样的功能，都是计算三角函数，而所用的方法也一样，都是泰勒展开。至于微软为什么不直接使用c++提供的math库函数，而非要再造一个轮子来计算这类函数，我个人猜测可能有两个原因，一个是历史遗留问题，也许早年c++还没有math库，另一个我觉得使用库函数的话会造成编译出来的二进制文件过大，也许微软也担心这个问题。当然这都是我个人的猜测，但这里不做重点讨论。

其实，计算器求解我们所知道的几乎所有的函数都是使用泰勒展开方法，例如   ,   ,   等等。

那么泰勒级数为什么能逼近我们我们所需要的函数曲线呢？为了解决这个问题，我们先从一个简单速度的问题说起。

假设小明坐在一辆车上，车的行驶速度随时间   变化为   .小明突然很想知道当   时刻他的行驶速度。这可把小明给难住了，因为他手上没计算器，又没三角函数表可查。如果是特殊的函数点位的话，大不了他运用运用和差公式直接就可以计算出来，但是这种情况该怎么办呢？

万般无奈的小明想到，如果我能把这个速度指数函数转化成只有加法或者乘法的函数，那该多好。

小明想到，如果定义一个只有加法乘法的函数   ，让它在某点的值与   的值一样，后面为了保证它们两个的增长趋势一样，让它们两个的速度的变化率（导数）一样，变化率的变化率（导数的导数）也一样，变化率的变化率的变化率（导数的导数的导数）也一样。。。，那么后面的两者函数的值不应该是很接近吗？ 在一定条件下成立呢？

于是，小明定义了一个只有加法与乘法的函数   来表示所有可能的多项式：  可是如何才能让g(x)逼近f(x)呢，换句话说，如何取得合适的   才能让  成立呢？

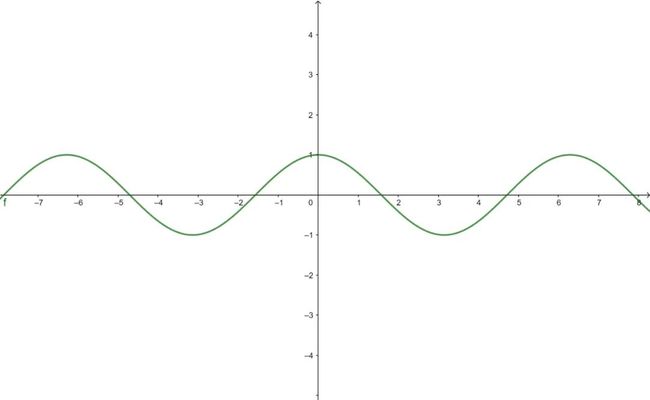
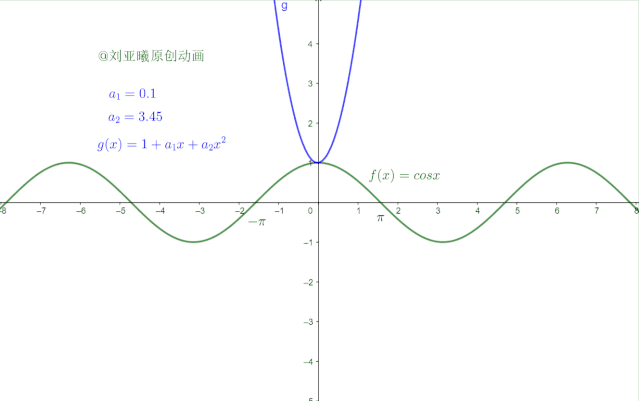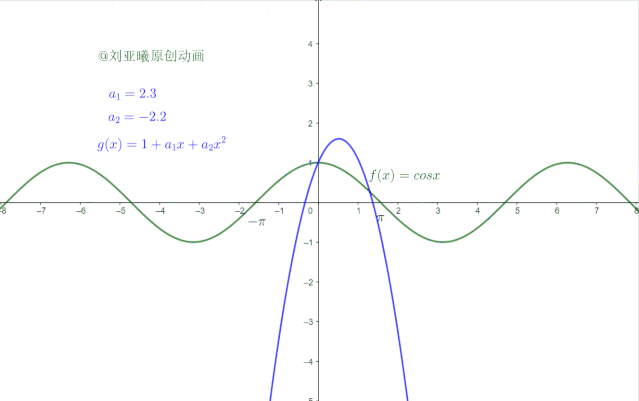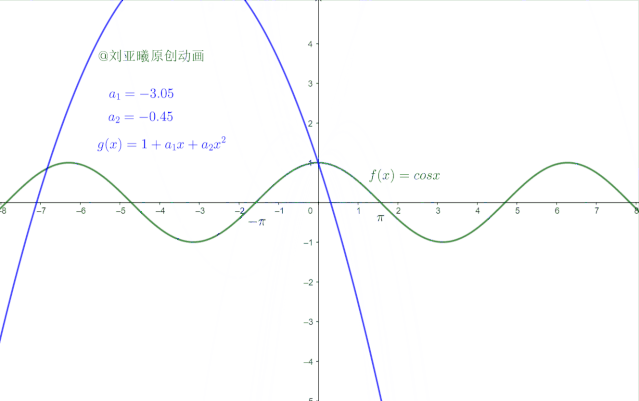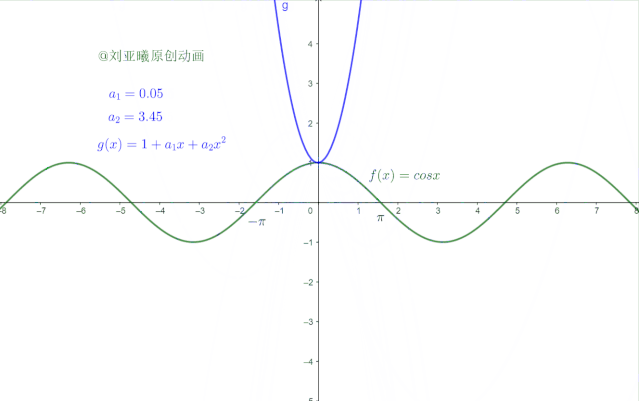
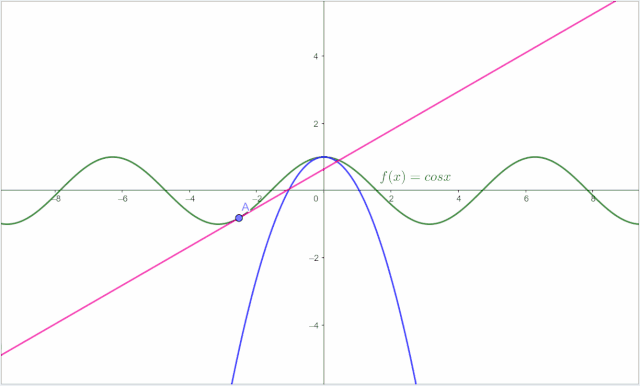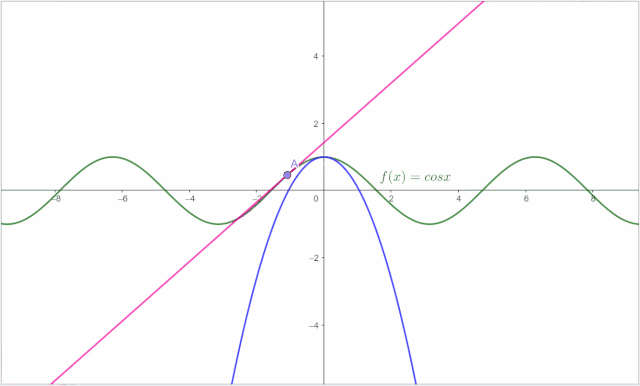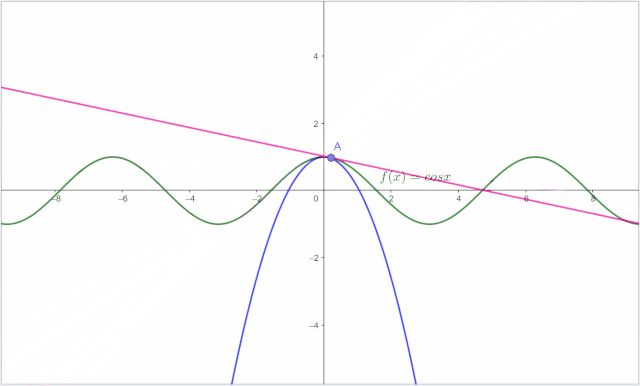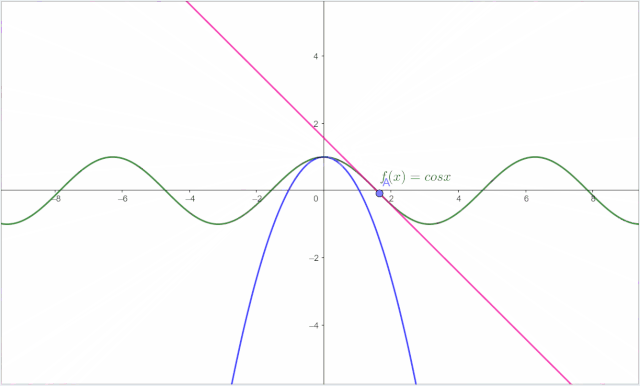
小明观察了   的函数图像：

他发现，在(-π,π)区间之内，   函数的图像很像抛物线。舍繁取简，他也用抛物线来近似。于是他讲   简化，定义为： 

可即便这样，还是要找出三个变量的值。于是小明进一步思考，已经知道   了，求得的   至少也得让他们两者在   处相等，也即：  代入计算：

也即   变成：  可是在那么多的   与   当中，如何取值呢？

于是，小明再观察图像，他为了保证在   附近这个抛物线逼近   ，他让两者的切线斜率一致，这样就保证了两个函数的加速度保持一致，也即： 

代入计算：  也即   ，这样   也就更简单了，直接剩下最后一个系数：  这时候小明再观察图像，发现两者似乎又进了一步：

为了求出最后一个   ，小明再观察图像：

小明发现在   附近，也即(-π/2,π/2)附近，   是一个凸函数，而且斜率不断减小，这时为什么不让他们的斜率的增长率也保持一致呢？也就是说让两个函数在   处加速度的加速度也相等，也即他们的二阶导数相等：  代入计算：  求得   ，从而得到  再观察图像：

这时候发现，经过三次的求导运算，两者函数在   周围已经非常接近了。我们来实际验证一下用   逼近   的误差有多大：    两者误差仅为0.00005，完全在我们可接受的范围之内。于是乎，小明忽然明白了为什么   与   是等价无穷小了（当初的我曾经对这个公式大惑不解）。

可是小明依旧不满足，他在想我只求了两次的倒数，如果我让变化率的变化率的变化率的变化率的变化率。。。。也相等的话，误差会不会更小呢？

于是小明持续往下计算

发现越往后，越精确，但是代价就是计算量越大。而往往，我们直接舍去后面的高阶无穷小，仅需要前三四项即可满足我们的要求。

可是，小明突然又想到，这样只是计算在   处附近的函数值，如何让   逼近   的任意一点比如   呢？很简单只要将   替换成   即可，推导过程也一样，只是不会像x=0处那样把奇数项给消掉了：

小明大喜，用这种方法在没有计算器的情况下几乎可以计算任何函数的数值了，虽然有一定误差，但误差完全在我们容忍范围之内。于是他又用同样的方法计算了   在   处的泰勒展开：

具体步骤为：

1),先让函数值相同，也即  得到：   2),再让一阶导数相等 

得到：  ......

最后让n阶导数数相等 (   的   阶导数仍是   )

得到：  最后得出：

当   不断增大的时候，小明惊奇地发现在固定区间内，两者几乎完美地融合在了一起：

可是小明纵然知道了其中的推导原理，但他依然不太直观理解泰勒级数为什么会逼近原函数。我在上文「深入浅出线性代数的理解及应用」中曾经引用笛卡尔的名言，说明几何对抽象代数理解的重要性。同样，在这里也不例外，泰勒级数在几何上也有明确的意义：

泰勒级数的几何意义

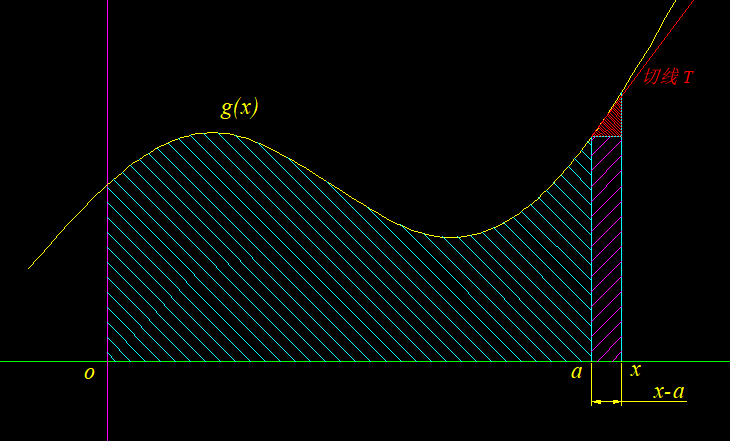
如图下所示，我们假设黄色的曲线函数为   ，在   区间内连续。点   为点   周围（微小的邻域）内任意一点。

我们再定义一个积分函数：  由于   是   的原函数（注意，   是积分函数，   才是曲线函数），因此： 

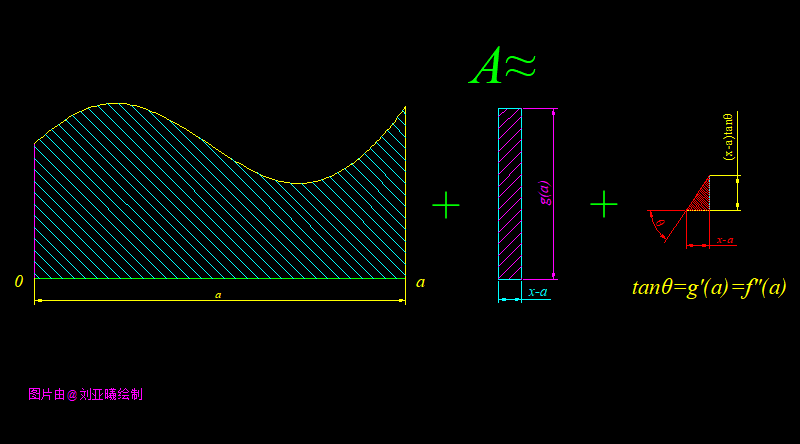
积分函数   连续，因此可以分成两个积分区间：  这两个积分区间实际上由三部分构成。根据积分的实际几何意义，我们知道   代表图中阴影部分的面积，我们记为   .而面积A由三部分构成，分别是   扫过的曲边多边形  ～  ，矩形   ，曲边三角形   ：

我们记三部分面积分别为  ～  ，也即：

～

曲线   在任意一点的切线斜率为   ,曲边三角形的斜边我们可以用   在点   上的切线来近似表示（这便是我在上篇文章深入浅出线性代数的理解及应用中提到的微分的“非线性函数的局部显性化”的重要思想）。显然，这里在   处斜率为   ，也即   .如果   越接近   ，那么这个斜边越接近曲线   ：

切线   在点   处的斜率为   ，也即   ，因此三角形的直角边高   为：  θ 从而得出三角形的面积为：  也即  而这个矩形的高即   ，它的面积： 

也即：  显然曲边多边形也就是第一部分的面积为   :  ～ 三个面积相加，也就是 

上面这个式子不正是泰勒级数展开的二次多项式吗，不过不要忘了，这个式子与   之间的关系是约等于。如果   无限逼近   ，那么我们完全可以用   来近似   ,也就是说省略掉后面的矩形与三角形，只剩下一项。而实际上我们省略了后面的高阶无穷小，在一般情况下，精度已经够高了。

这便是泰勒级数在几何上面的解释。

推荐阅读：

    专辑|Linux文章汇总

    专辑|程序人生

    专辑|C语言

嵌入式Linux

微信扫描二维码，关注我的公众号