循环队列的定义,入队算法,出队算法,遍历算法,及其代码实现
队列 的定义:
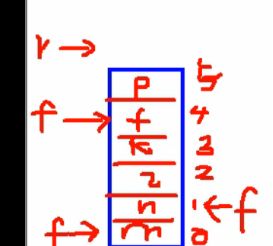
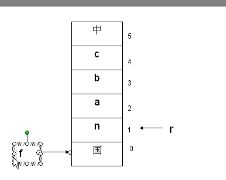
一种可以是实现“先进先出”的存储结构。数据的进出类似于排队购票。队只允许队尾一端(rear)添加,在另一端队头(front)删除。队有队头(front)和队尾(rear)两个指针。队头front指向第一个元素,队尾rear指向无实际意义的元素,即队列最后一个元素的下一位置。
//队列定义
typedef struct Queue
{
int *pBase;//数组基地址,数组的首地址
int front;//队头
int rear;//队尾巴
}QUEUE;
//创建一个队列,空间分配,保存6个整形元素。
void init (QUEUE *pQ)
{
pQ->pBase=(int*)malloc(sizeof(int)*6);//长度为6的数组
pQ->front=0;
pQ->rear=0;
}
队列的分类:
分为动态队列和静态队列两种。动态队列用链表实现。动态队列易于实现。静态队列用数组实现,静态队列通常都必须是循环队列。
- 静态队列为甚么必须是循环队列?
数组实现静态队列,删除元素时候,每删除一位,front指针上移一位,浪费一个单位的数组空间。这种方式添加元素的时候rear上移一个,删除元素的时候front上移一个。总之都是上移。
当front或者rear指到最上面一个位置,再上移就移动到最下面一个位置。所以数组实现队列的时候必须是循环队列,传统方式实现不了。
2.循环队列需要几个参数来确定,及循环队列各个参数的含义
队列需要两个参数确定,front和rear.2个参数不同的场合有不同的含义,建议初学者先记住,然后慢慢体会。
- 队列初始化
Front和rear的值都是零
- 队列非空
Front 代表的是队列的第一个元素
Rear代表队列的最后一个有效元素的下一个元素
- 队列空
Front 和rear的值相等,但不一定是零。
2.循环队列入队伪算法讲解
Rear=(rear+1)%数组的长度
//进队,队尾rear+1;
bool en_queue(QUEUE *pQ,int val)
{
if(full_queue(pQ))
{
return false;
}
else
{
pQ->pBase[pQ->rear]=val;
pQ->rear=(pQ->rear+1)%6;
}
}
- 循环队列出队伪算法讲解
Front=(front+1)%数组的长度
//出队,队头位置变为:(front+1)%6
bool out_queue(QUEUE *pQ,int *pVal)
{
if(emput_queue(pQ))
return false;
else
{ *pVal=pQ->pBase[pQ->front];
pQ->front=pQ->front+1;
return true;
}
}
4.判断循环队列是否已空
Front与rear的值相等,则该队列为空。
5.如何判断循环对了是否已满
预备知识 :由于是循环队列,front的值可能比rear大,可能比rear小,也能相等,两者没有规律。但是队首旋转的速度不能比队尾快。
当存放元素的数目等于数组的存储位置个数,则rear和front重合。分不清头和尾。
所以我们少用一个存储位置。
c语言伪算法表示是:
队列满的条件:if ((rear+1)%数组长度==front)已满
Else 不满
#include
#include
#include"stdbool.h"//解决不能使用bool
#include "malloc.h"
//队定义
typedef struct Queue
{
int *pBase;//数组基地址,数组的首地址
int front;//队头
int rear;//队尾巴
}QUEUE;
void init(QUEUE*);//创建循环队列
bool en_queue(QUEUE*,int ); //入队
void traverse_queue(QUEUE*);//遍历
bool emput_queue(QUEUE* );//队是否满
bool full_queue(QUEUE *);//对列是否空
bool out_queue(QUEUE *,int *);//出队
int main()
{
int Val;
QUEUE Q;
init(&Q);
en_queue(&Q,1);
en_queue(&Q,2);
en_queue(&Q,3);
en_queue(&Q,4);
en_queue(&Q,5);
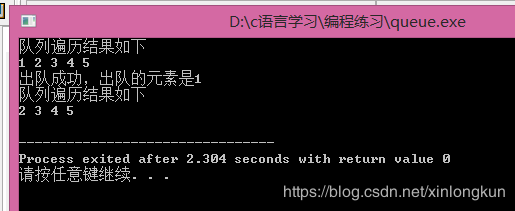
traverse_queue(&Q );//遍历
if(out_queue(&Q ,&Val))
{
printf("出队成功,出队的元素是%d\n",Val);
traverse_queue(&Q );//遍历
}
return 0;
}
//创建一个队列,空间分配,保存6个整形元素。
void init (QUEUE *pQ)
{
pQ->pBase=(int*)malloc(sizeof(int)*6);//长度为6的数组
pQ->front=0;
pQ->rear=0;
}
//判断循环队列是否满
bool full_queue(QUEUE *pQ)
{
if((pQ->rear+1)%6==pQ->front)
{
return true;
}
else
return false;
}
//进队,队尾rear+1;
bool en_queue(QUEUE *pQ,int val)
{
if(full_queue(pQ))
{
return false;
}
else
{
pQ->pBase[pQ->rear]=val;
pQ->rear=(pQ->rear+1)%6;
}
}
//利用中间变量,遍历队列
void traverse_queue(QUEUE *pQ)
{
printf("队列遍历结果如下\n");
int i= pQ->front;
while(i!=pQ->rear)
{
printf("%d ",pQ->pBase[i]);
i=(i+1)%6;
}
printf("\n");
return ;
}
bool emput_queue(QUEUE* pQ)
{
if(pQ->front==pQ->rear)
return true;
else
return false;
}
//出队,队头front+1
bool out_queue(QUEUE *pQ,int *pVal)
{
if(emput_queue(pQ))
return false;
else
{ *pVal=pQ->pBase[pQ->front];
pQ->front=(pQ->front+1)%6;
return true;
}
}