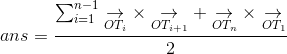学习笔记第十四节：向量、叉积、点积，旋转卡壳及其应用

正题

      向量看起来很难，但是理解透彻，运用得好，在比赛上会占很大优势。

      首先我们描述一个二维向量，用两个坐标表示，它是有方向的，我们可以把它平移回原点，那么他的坐标就只有两个了，。

 

向量的缩放

      把向量缩放为原来的k倍，

向量的叉积

      向量的叉积是一个向量，即，向量p的模长的绝对值为AB与AC为邻边所组成的平行四边形的面积。

      正负性由AB在AC的顺逆时针方向决定，当AB在AC的顺时针时，p的模长为正；逆时针时，模长为负。

向量的点积

      向量的点积是数量积，即。几何意义上为AB在AC上投影的长度，乘上AC的模长。

      那么我们会这几个东西，我们就可以去学凸包了。贴自己博客真的是不要脸

      学完这个以后，我们还要拓展一些东西。

向量的旋转

      

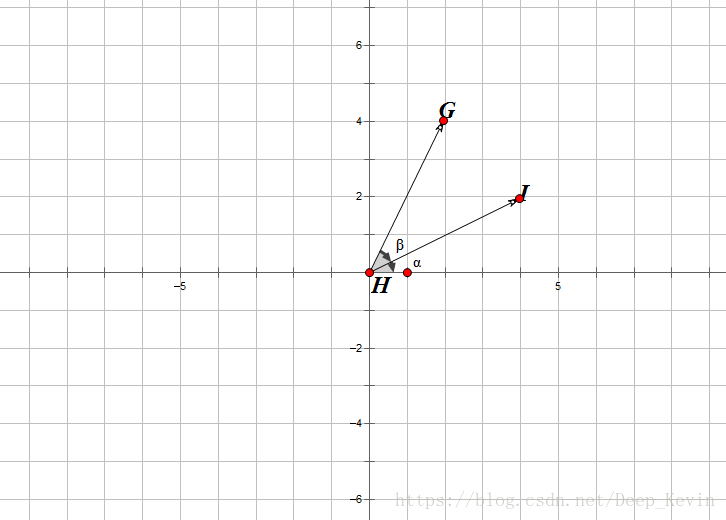
      我们一直向量HI，现在要求向量HI逆时针旋转β之后的向量HG。

      ，l为HI的模长

      那么我们就要求.

      和角公式证明即可。

      得出。（这个在比赛中很有用，有兴趣的同学可以试着从点积的方向去证明。）

直线的交点

      这个就很明显了，已知两条直线

                                                                                          

      很明显他们交点的坐标就是解这个方程

                                                                                         

      解得

                                                                                         

线段的交点

      我们首先可以求出来两条线段所在直线的交点，然后再判断这个交点是否在两条线段上，如果是，那么就有交点，否则就没有交点。

      第二种方法可以用叉积来判断，首先判断以每条线段的两个端点所构成的举行是否相交，如果是，那么用叉积判断每条线段是否在另一条线段所在的直线上，否则没有交点。

任意多边形的面积

       有一个结论就是.，O为任一点

       其中乘号表示的是叉积，我们知道一个在外面的点x，沿着Ox的方向，从x开始，会穿过多边形边界偶数次。

       所以在叉积相当于，正着算一遍反着算一遍，相当于没有。

       而那些在里面的，恰好会被算单数次（正数）。

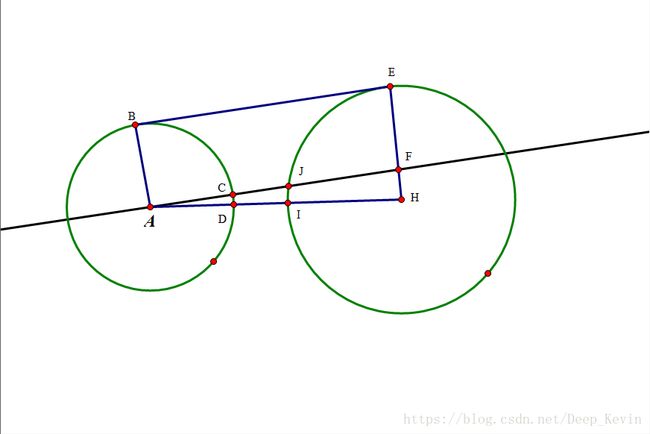
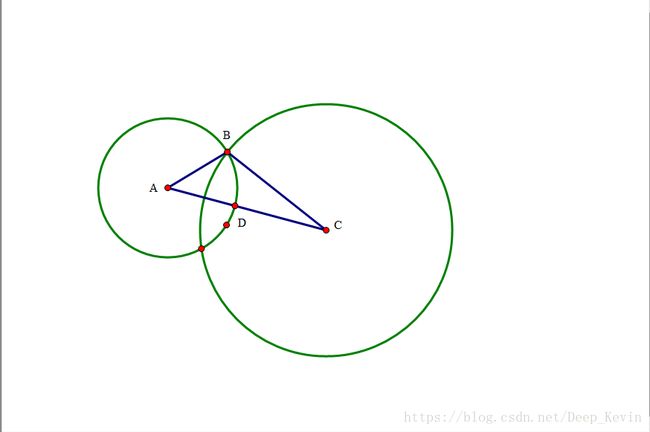
圆的内公切线与圆的交点

       

      如上图，已知两个圆，求A点的坐标。

      我们只得到BD的长度，AB和DE的长度，就很容易求BC的长度。因为三角形ABC与三角形EDC相似，所以

      然后我们知道了AB和BC还有一个直角，就可以用acos来求出∠ABC的大小。

      再把BC缩放到BF那么长，就可以通过旋转来求出A点的坐标了。

      E点同理。

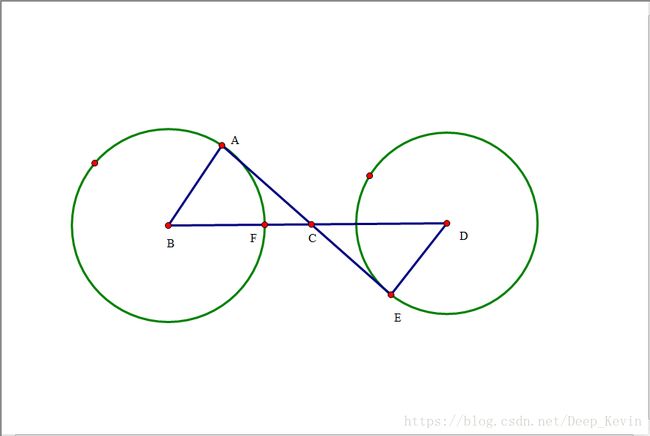
圆的外公切线与圆的交点

      

      如上图，已知两圆，求外公切点。

      我们可以知道AH和HF（两圆半径之差），就可以用asin来算出∠FAH的大小，我们再把AH缩放到AD的长度，再把它旋转∠DAC+90°即可。

两圆交点

      

      已知两个圆，求交点坐标。

      很简单啊，已知AB，BC，和AC。就可以用余弦定理求出∠BAC的大小，然后再把AC缩放到AD，旋转∠BAC即可。

点到直线的距离

       套公式

       

      即可算出。

点到圆的距离

       直接用点到圆心的距离减去圆的半径就可以了。

旋转卡壳

       重点来了。

       对于一个凸多边形（不是凸多边形先求凸包）。

       我们思考怎么通过On的时间来寻找最大距离点对。

       在朴素算法中，我们习惯直接在凸包上找最远点来求解。

       很慢。

       但是，我们可以发现一个规律，就是如果我们询问的点是顺时针的，每个点所对应的最远点，也是按照顺时针进行排列的。

       所以很明显，我们就可以用一个now来存储最远点当前的位置，如果最远点的下一个点比最远点远的话。

       那我们就可以最远点++

       一直到距离相等或者距离变小。

       这时候，更新就可以了。

       

#include
#include
#include
#include
#include
using namespace std;

int n;
struct node{
	double x,y;
}s[10000010];

double dou(double x){
	return x*x;
}

double dis(int x,int y){
	return sqrt(dou(s[x].x-s[y].x)+dou(s[x].y-s[y].y));
}

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%lf %lf",&s[i].x,&s[i].y);
	int now=1;
	double mmax=0;
	for(int i=1;i<=n;i++){
		while(dis(i,now)

旋转卡壳的经典应用

       我们旋转卡壳的应用还有很多很多。（很逗很逗）

       比如说，要求多边形的宽度（字面意思）

      这时，把里面的max改成min就可以了。

      还有比如说，要求两个凸多边形的最远点对，也是两个顺时针转，就可以了。

      最近点对我觉得其他博客上写的都有问题。

       觉得只能用kdtree。

       kdtree和替罪羊还有闵可夫斯基和也是非常有用的