主动噪声控制(ANC)与Simulink仿真
主动噪声控制与Simulink仿真
- 摘要
- 空气管道问题
- X-滤波的LMS算法
- 反馈路径
- 其它ANC模型
- Simulink仿真实验与结果
- 真实环境
- 参考资料
摘要
随着数字信号处理器的发展,近年来主动/有源噪声控制(Active Noise Control, ANC)技术已在耳机、汽车等领域普及。
本质上,主动噪声控制的目的是产生与噪声信号相反的声波,以抵消/削弱噪声。但是由于目前中文网络上对于具体实现的介绍尚不完善,笔者希望更透彻地解析其中一些能引发思考且不可忽视的细节。
本文基于Matlab官方给出Simulink例程,主要介绍宽带前馈单通道ANC系统原理,和X-滤波的LMS算法思想,并简单拓展到其它类型的ANC系统。
空气管道问题
ANC的一个典型应用场景是空气管道,例如空调(HVAC)管道或者是汽车的排气管道。
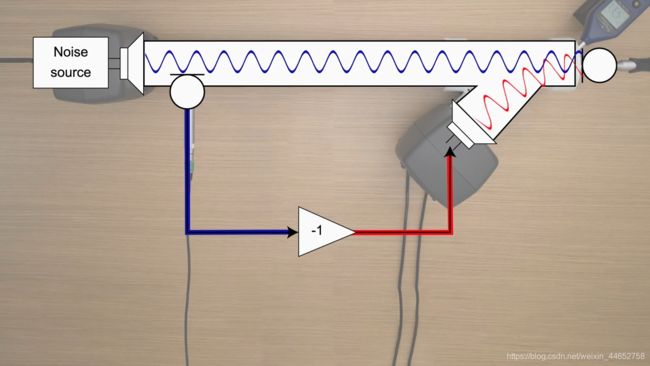
上图展示了一个理想化的空气管道ANC系统,左侧的圆圈是参考拾音器(Reference Microphone),它接收蓝色的噪音,然后取其声压的相反数,从对消扬声器输出红色的相反信号。如果在右侧的误差拾音器(Error Microphone)拾取到的声音接近与0,则再往右侧的管道中声信号也被抑制,也意味着达到了我们的目标。
但是,事情远没有这么简单。显然,噪声从参考拾音器处经过后,到与对消扬声器相遇还行经了一段距离,在这段距离里,噪声信号经历了时延、衰减、混响等调制。这些经历使得它已经不是原来被拾取的噪声信号,所以单纯的取相反数难以保证完美的抵消。
这时就需要用上误差拾音器的结果,对这段经历进行估计,然后对参考拾音器拾取到的信号添加这样的估计,再取相反数,发送给对消扬声器。
从参考拾音器到误差拾音器的这段空气管道经历,记作主路径(Primary Path),用传递函数 P ( z ) P(z) P(z)表示。而对经历的估计并取反,用传递函数 W ( z ) W(z) W(z)表示。(注意,为了方便起见,这里都使用离散形式的传递函数表达式)
这个估计是可以随时调整的,调整的算法是归一化的最小均方(Normalized Least Mean Square, NLMS)算法。NLMS算法的作用就是对某一系统进行估计,其算法在笔者之前讲AEC算法的博文中简单探讨过,这里不再展开。
所以这样就好了吗?并不。事实上,从对消扬声器到误差拾音器之间,还有一段传播过程,尽管我们可以通过将误差拾音器和对消扬声器放得很近,但始终不能忽略这一过程。从扬声器到误差拾音器的这一过程叫做次路径(Secondary Path),传递函数记作 S 2 ( z ) S_2(z) S2(z)
X-滤波的LMS算法
X-滤波(Filtered-x)则用于对次路径作出调整。
我们考虑如下的一个含主次路径的系统框图。如前所述, P ( z ) P(z) P(z)、 W ( z ) W(z) W(z)和 S 2 ( z ) S_2(z) S2(z)分别表示空气管道传递函数、自适应滤波器传递函数和次路径传递函数。

如果基于这个系统求解 W ( z ) W(z) W(z),有:
W ( z ) = − P ( z ) S 2 ( z ) W(z)=-\frac{P(z)}{S_2(z)} W(z)=−S2(z)P(z)
并不是一个可行解。
然而,如果我们假定(在很短的时间内) W ( z ) W(z) W(z)和 S 2 ( z ) S_2(z) S2(z)都是线性时不变系统,则可以调换二者的顺序,形成如下的近似:

这也就是说,我们可以先对输入噪声x进行(近似的)次路径滤波,再送给LMS算法进行自适应迭代,等价于先经过自适应的滤波,再通过次路径。这也是其名X-滤波算法的原因。
于是就有了以下的算法框图:

值得注意的是,这里加入的依然是对次路径的估计 S 2 ′ ( z ) S'_2(z) S2′(z),这样的估计需要在ANC系统工作开始前获得。其获得方法是:让对消扬声器播放白噪音,作为待测系统输入,误差拾音器接收信号,作为待测系统输出,用LMS算法进行估计。
反馈路径
至此,我们仍未考虑的一点是:当对消扬声器播放声音时,不单是误差拾音器能收到声音,参考拾音器仍能拾取扬声器的声音。显然,这会干扰到对源噪声 x ( n ) x(n) x(n)的估计。
而从对消扬声器到参考拾音器这一部分,称为反馈路径,传递函数记作 F ( z ) F(z) F(z) 或 S 1 ( z ) S_1(z) S1(z)
因此,同样地,在ANC系统工作开始前需要获得反馈路径的估计,再从参考拾音器中减去对消扬声器声音的近似 F ′ ( z ) F'(z) F′(z) 。

值得注意的是,在Matlab官方给出的完全电脑模拟的Simulink例程中,没有对于反馈路径的考虑。
其它ANC模型
至此,我们讲完了一整个空气管道模型。这个模型又称为宽带前馈单通道ANC模型。其中:
- 宽带:指的是理论上可以抵消所有频率的声音。对应的窄带ANC模型,其输入噪声源并不是通过拾音器录制的信号。而是在已知目标噪声的频率时,产生该频率的脉冲串作为 x ( n ) x(n) x(n)。因此只能抵消某几段频率的噪声,即为窄带ANC,见下图1.
- 前馈:指的是误差拾音器向前对扬声器进行反馈。对应的反馈模型,则是先用误差拾音器收音,扬声器从后先前对误差拾音器周围的环境进行反馈,见下图2.
- 单通道:指的是不论所使用的扬声器或拾音器均为单通道。相应地,如果空气管道过于庞大,则需要考虑在管道侧面的各个方向上增加输入/输出通道,见下图3.


Simulink仿真实验与结果
为方便起见,这里借助Matlab官方给的实验框架。
在含有的Audio Toolbox与Simulink内容的Matlab中,官方框架可以通过执行以下语句直接调用:
%% Secondary Path Estimation Model ----- 次路径估计
open_system('SecondaryPath_ANC')
sim('SecondaryPath_ANC')
%% Filtered-X ANC Model ----- X-滤波ANC模型
open_system('FilteredX_LMS_ANC')
sim('FilteredX_LMS_ANC')
笔者主要进行了第二个实验,即已知次路径的估计,模拟X-滤波模型。其中的次路径参数遵循例程的初始设定:
真实滤波器系数:[0.5 0.5 -.3 -.3 -.2 -.2]
估计滤波器系数:[0.466 0.533 -0.257 -0.274 -0.231 -0.175]
此处的误差有可能影响之后对于主路径的估计,进而可能影响ANC的收敛。
在这样的条件下,笔者引入三种不同的信号,尝试不同的组合:
其中从上到下分别是,白噪音、(多个)正弦波组合、一段电台对话录音。
对应波形图(依次黄、蓝、红)如下:
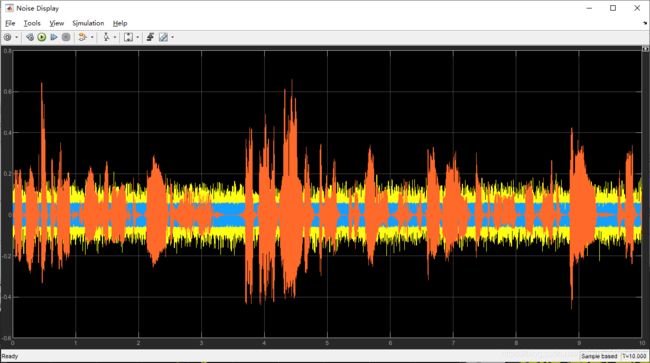
结果不论是何种组合,都能得到良好的降噪效果,此处只展示三种声音混合叠加
(注:下图中,黄色为经过主路径后的噪声,蓝色为对消后误差拾音器得到的噪声,时长10秒,采样率8820Hz)

该实验允许使用者实时地听到降噪效果。实验内容的slx文件,可以在笔者的Github项目下载到。
真实环境
以上结果说明,在全部模拟环境下,我们能取得相当不错的效果。
那么到实际环境下呢?我们的计算机是否有足够的计算速度完成模数/数模转换,计算等过程?在实际中的降噪效果又如何呢?
参考Matlab官方的实验结果,他们使用了长度34厘米的PVC管实验环境:

以及Speedgoat硬件对模拟信号进行处理。据称,此机器的时延低至1~2个采样点。
官方并没有给出噪声随时间变化的展示。
但是他们的结论是:
We have measured the performance of this ANC prototype with both dual tones and the actual recording of a muffled washing machine. We obtained a noise reduction of 20-30 dB for the dual tones and 8-10 dB for the recording, which is a more realistic but also more difficult case. The convergence rate for the filter is less than a few seconds with tones, but requires much more time for the real case (one or two minutes).
意思是,双纯音噪声可以降低20到30分贝,而且只需要学习几秒便可。但是对于录制的(低沉的)洗衣机噪声,则只能降低8-10分贝,且需要一两分钟进行学习,
另外,实验人员还提到了扬声器带来的时延问题。扬声器的迟钝使得他们只有约0.3ms(2.5/8)进行模数转换、ANC滤波和数模转换。
所以,如果需要将这个模型应用到降噪耳机,一个管道长度显著小于本实验的环境。则必须更换更灵敏的扬声器。
参考资料
- 书籍:自适应滤波器原理及Matlab仿真应用(原书第2版) 机械工业出版社
- 网页:Active Noise Control with Simulink Real-Time
- 视频:Active Noise Control – From Modeling to Real-Time Prototyping


