凸包算法分析

toleft:
对于toleft的计算，是通过叉积的定义来进行的，叉积代表面积，且方向为顺时针，那么如果大于0，则认为k在ab向量的左边.
对于2个向量a(x1,y1),b(x2,y2),将其进行行列式的计算，第三维补0，计算过程如下：

而2个二维向量可以由3个点a(x1,y1),b(x2,y2),k(x3,y3)相减得到，然后我们可以得到计算公式：

//通过向量叉乘符号来进行定义 ,必须严格大于0，在一条线上的也不算left 
bool toleft(Point a, Point b, Point k)
{
    return (a.x * b.y - a.y * b.x + b.x * k.y - b.y * k.x + k.x * a.y - k.y * a.x) > 0 ? true : false;
}

in_triangle:
有了toleft（），我们可以进行点是否在多边形内的判断，比如三角形的话，点在内部则3对3边顺时针进行toleft测试要么都在左要么都在右。

bool in_triangle(Point a, Point b, Point c, Point k)
{
    bool r1 = toleft(a, b, k);
    bool r2 = toleft(b, c, k);
    bool r3 = toleft(c, a, k);
    return (r1 == r2) && (r1 == r3);
}

我们进行凸包的计算，算法有多种，从O(n^4) ~ O(nlogn)
一、EP（extreme point）算法（O（n^4））
极点：不被任何图形内点构成的三角形所包含的点为极点，通过排除法来找极点。步骤：
1. 全部点表为极点
2. 对每一个点，通过对每个可能的三角形进行in_triangle测试，如果没有一个三角形能包含此点，那么此为极点，否则标记为非极点。

二、EE（extreme edge）极边算法（O（n^3））
极边：图中所有点都在其一侧的边称为极边，可以通过toleft测试判断。步骤：
1、对图中每一条边，对除构成此边2点的其他点进行toleft测试，如果全为false或者全为true，证明所有点都在其一侧，标记为极边。

//返回extreme edge的个数
int EE(Point *a, Point *res, int num)
{
    int res_count = 0;
    for (int i = 0; i < num; i++)
        for (int j = i + 1; j < num; j++)
        {
            bool flag;
            int count = 0,result = 0;
            for (int k = 0; k < num ; k++)
            {
                if (k == i || k == j)
                    continue;
                if (count == 0)//第一个点，确定左右
                {
                    flag = toleft(a[i], a[j], a[k]);
                    count++;
                }
                else if (flag != toleft(a[i], a[j], a[k]))//有一个点与前面点不同
                {
                    result = 1;
                    break;
                }
            }
            if (result == 0)//证明全部点都在a[i] a[j]边的一边
            {
                res[res_count++] = a[i];
                res[res_count++] = a[j];
            }
        }
    return res_count / 2;
}

三、Javis march（O（hn））
根据EE的想法，我们可以想到一个凸包所有的边都是连着的，那么在找到一条边之后我们可以顺着其中的顶点继续向下找，而不用将所有的边都进行遍历。步骤：
1. 找到最左下的点LTD->p_now
2. 从p_now出发找到第一条极边FEE，并将另一个顶点赋为p_now
3. 不断重复2步骤，直到p_now = LTD，算法结束

//Jarvis Marching
int JM(Point *a, Point *res, int num)
{
    int min_x = INF,min_loc,min_y;
    //find ltl(最左下) Point to be the first element in stack s
    for (int i = 0; i < num; i++)
        if (a[i].x < min_x)
        {
            min_x = a[i].x;
            min_y = a[i].y;
            min_loc = i;
        }
        else if (a[i].x == min_x && a[i].y < min_y)//横坐标一样，取纵坐标小的那个
        {
            min_x = a[i].x;
            min_y = a[i].y;
            min_loc = i;
        }
    //将p1得到并放到第一个的位置，这样好操作 
    int flag = min_loc,end = flag;
    int count = 0;
    res[count++] = a[min_loc];
    while (flag != end || count == 1)
    {
        int right_most;//为了防止right_most == flag.
        if (flag == num - 1)
            right_most = flag - 1;
        else
            right_most = flag + 1;
        for (int i = 0; i < num; i++)//找到a[flag]点最右下的点，那么就是其下一个点，扫一遍即可，一直往toleft的反方向扫
        {
            if (i == right_most || i == flag )
                continue;
            if (!toleft(a[flag], a[right_most], a[i]))//证明a[i]比a[right_most]还要右下
                right_most = i;
        }
        res[count++] = a[right_most];
        flag = right_most;
    }
    return count;

}

算法复杂度为O（hn），其中h为凸包中点的个数，此算法当h很小（即大部分点全在凸包内）的时候可以认为其为O（n），当h很大的时候（如点全部都在凸包上）则为O（n^2）,是一个和最终结果相关的算法。

四、grahamscan（O（nlogn））：
算法步骤
1. 找到最左下的那个点LTD
2. 将剩余点根据与LTD点的角度大小从小到大排序（一般算tan的值）
3. 按照排序后的序列每次找到最右边的点（这个通过2个栈+toleft测试来实现）

int graham_scan(Point *a, Point *res, int num)
{
    stack S;
    stack T;
    float tanp[1000];
    float min_x = 1000000;
    float min_y = 1000000;
    int min_loc = -1;
    //find ltl(最左下) Point to be the first element in stack s
    for (int i = 0; i < num; i++)
        if (a[i].x < min_x)
        {
            min_x = a[i].x;
            min_y = a[i].y;
            min_loc = i;
        }
        else if (a[i].x == min_x && a[i].y < min_y)//横坐标一样，取纵坐标小的那个
        {
            min_x = a[i].x;
            min_y = a[i].y;
            min_loc = i;
        }
    //将p1得到 
    First_p = a[min_loc];
    //将后面元素向前移动，即提取First_p元素 
    for (int i = min_loc; i < num - 1; i++)
        a[i] = a[i + 1];
    num = num - 1;
    //按照angle来进行排序
    qsort(a, num, sizeof(Point), cmp);
    S.push(First_p);
    S.push(a[0]);
    for (int i = num - 1; i > 0; i--)
        T.push(a[i]);
    while (1)
    {
        if (T.empty())
            break;
        Point p2 = S.top();
        S.pop();
        Point p1 = S.top();
        S.pop();
        Point p3 = T.top();
        T.pop();
        if (toleft(p1, p2, p3))
        {
            S.push(p1);
            S.push(p2);
            S.push(p3);
        }
        else
        {
            S.push(p1);
            S.push(p3);
        }
    }
    int num_res = S.size();
    for (int i = 0; i < num_res; i++)
    {
        res[i] = S.top();
        S.pop();
    }
    return num_res;
}

算法复杂度主要集中在排序过程中为O（nlogn）。如果不排序直接乱序进行toleft测试的话，会出问题，比如：

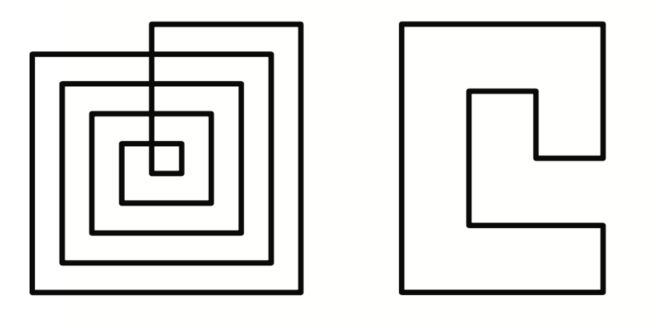
如果按照上面的图形的顺序（顺时针）进行grahamscan的话，那么找出来的凸包会就是原图形，所以不经过犄角排序是不行的。