HDU1007 查找平面最近点对
设p1=(x1, y1), p2=(x2, y2), …, pn=(xn, yn)是平面上n个点构成的集合S,设计算法找出集合S中距离最近的点对。
OJ题目:HDU1007http://acm.hdu.edu.cn/showproblem.php?pid=1007
1、蛮力法(适用于点的数目比较小的情况下)
1)算法描述:已知集合S中有n个点,一共可以组成n(n-1)/2对点对,蛮力法就是对这n(n-1)/2对点对逐对进行距离计算,通过循环求得点集中的最近点对:
2、分治法
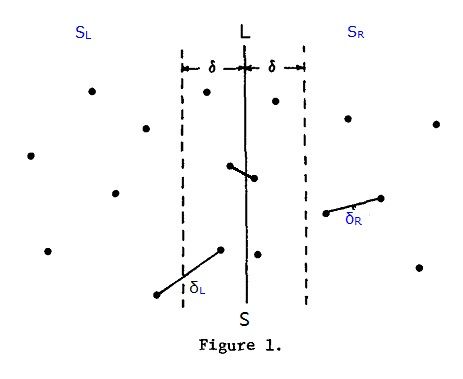
1)算法描述:已知集合S中有n个点,分治法的思想就是将S进行拆分,分为2部分求最近点对。算法每次选择一条垂线L,将S拆分左右两部分为SL和SR,L一般取点集S中所有点的中间点的x坐标来划分,这样可以保证SL和SR中的点数目各为n/2,
(否则以其他方式划分S,有可能导致SL和SR中点数目一个为1,一个为n-1,不利于算法效率,要尽量保持树的平衡性)
依次找出这两部分中的最小点对距离:δL和δR,记SL和SR中最小点对距离δ = min(δL,δR),如图1:
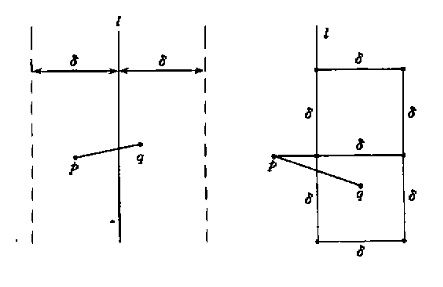
以L为中心,δ为半径划分一个长带,最小点对还有可能存在于SL和SR的交界处,如下图2左图中的虚线带,p点和q点分别位于SL和SR的虚线范围内,在这个范围内,p点和q点之间的距离才会小于δ,最小点对计算才有意义。
对于SL虚框范围内的p点,在SR虚框中与p点距离小于δ的顶多只有六个点,就是图二右图中的2个正方形的6的顶点。这个可以反推证明,如果右边这2个正方形内有7个点与p点距离小于δ,例如q点,则q点与下面正方形的四个顶点距离小于δ,则和δ为SL和SR中的最小点对距离相矛盾。因此对于SL虚框中的p点,不需求出p点和右边虚线框内所有点距离,只需计算SR中与p点y坐标距离最近的6个点,就可以求出最近点对,节省了比较次数。
(否则的话,最坏情形下,在SR虚框中有可能会有n/2个点,对于SL虚框中的p点,每次要比较n/2次,浪费了算法的效率)
#include
#include
#include
#include
#include
using namespace std;
struct point
{
double x,y;
}p[100005];
int a[100005];
int cmpx(const point &a,const point &b)
{
return a.x < b.x;
}
int cmpy(const int &a,const int &b)
{
return p[a].y < p[b].y;
}
double dis(int a,int b)
{
return sqrt((p[a].x - p[b].x) * (p[a].x - p[b].x) + (p[a].y - p[b].y) * (p[a].y - p[b].y));
}
double min(double x,double y)
{
return x < y ? x : y;
}
double cloest(int left, int right)
{
if(left == right)
return 1000000;
if(left + 1 == right)
return dis(left,right);
int mid = (left + right) >> 1;
double d1 = cloest(left,mid); //递归求左部分最近点距离
double d2 = cloest(mid+1,right); //右部分
double d = min(d1,d2);
int i,j,k = 0;
for( i = left ; i <= right; i++ )
{
if(fabs(p[mid].x - p[i].x) < d) //记录和mid位置点小于d的点的位置
a[k++] = i; //注意这里记录的是位置号
}
sort(a,a+k,cmpy); //按y坐标排序
for( i = 0; i < k - 1; i++ )
{
for( j = i+1; j < i + 7 && j < k; j++ )
{
if(p[a[j]].y - p[a[i]].y >= d)
break;
d = min(d,dis(a[i],a[j]));
}
}
return d;
}
int main()
{
int i,n;
while(scanf("%d",&n) != 0)
{
if(!n)
break;
for( i = 0; i < n; i++ )
{
scanf("%lf %lf",&p[i].x,&p[i].y);
}
sort(p,p+n,cmpx); //按x坐标排序
printf("%.2f\n",cloest(0,n-1) / 2);
}
return 0;
}