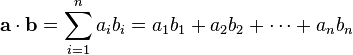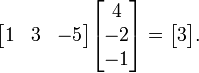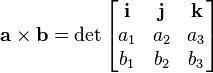叉积 ：也被称为 矢量积、 外积，是一种在 向量空间中 向量的 二元运算。与 点积不同，它的运算结果是一个 伪向量而不是一个 标量。并且两个向量的叉积与这两个向量都 垂直。
--------------------
定义：
点积：
两个(来自正交规范向量空间)向量 a = [a1, a2, … , an] 和 b = [b1, b2, … , bn] 的点积定义为:
这里的 Σ 指示总和符号。
例如，两个三维向量 [1, 3, ?5] 和 [4, ?2, ?1] 的点积是
使用矩阵乘法并把(纵列)向量当作 n×1 矩阵，点积还可以写为:
这里的 aT 指示矩阵 a 的转置。
使用上面的例子，这将结果一个 1×3 矩阵(就是行向量)乘以 3×1 向量(通过矩阵乘法的优势得到 1×1 矩阵也就是标量):
两个向量 a 和 b 的叉积写作 a × b （有时也被写成 a ∧ b，避免和字母 x 混淆）。叉积可以被定义为：
在这里 θ 表示 a 和 b 之间的角度（0° ≤ θ ≤ 180°），它位于这两个矢量所定义的平面上。而 n 是一个与 a 和 b 均垂直的单位矢量。
这个定义有一个问题，就是同时有两个单位向量都垂直于 a 和 b：若 n 满足垂直的条件，那么 -n 也满足。
“正确”的向量由向量空间的方向确定，即按照给定直角坐标系 (i, j, k) 的左右手定则。若 (i, j, k) 满足右手定则，则 (a, b, a × b) 也满足右手定则；或者两者同时满足左手定则。
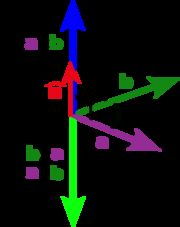
一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的：若坐标系是满足右手定则的，
当右手的四指从a以不超过180度的转角转向b时，竖起的大拇指指向是c的方向。由于向量的叉积由坐标系确定，所以其结果被称为伪向量。
给定直角坐标系的单位向量 i，j，k 满足下列等式：
- i × j = k j × k = i k × i = j
通过这些规则，两个向量的叉积的坐标可以方便地计算出来，不需要考虑任何角度：设
- a = a 1 i + a 2 j + a 3 k = [ a 1, a 2, a 3]
- b = b 1 i + b 2 j + b 3 k = [ b 1, b 2, b 3]
则
- a × b = [a 2b 3 ? a 3b 2, a 3b 1 ? a 1b 3, a 1b 2 ? a 2b 1]
上述等式可以写成矩阵的行列式的形式：
叉积也可以用四元数来表示。注意到上述 i，j，k 之间的叉积满足四元数的乘法。一般而言，若将向量 [a1, a2, a3] 表示成四元数 a1i + a2j + a3k，两个向量的叉积可以这样计算：计算两个四元数的乘积得到一个四元数，并将这个四元数的实部去掉，即为结果。更多关于四元数乘法，向量运算及其几何意义请参见四元数与空间旋转。
拉格朗日公式
- 这是一个著名的公式，而且非常有用：
- a × ( b × c) = b( a · c) ? c( a · b),
可以简单地记成“BAC - CAB”。这个公式在物理上简化向量运算非常有效。需要注意的是，这个公式对微分算子不成立。
这里给出一个和梯度相关的一个情形：
这是一个霍奇拉普拉斯算子的霍奇分解 
的特殊情形。
- 另一个有用的拉格朗日恒等式是：
这是一个在四元数代数中范数乘法 | vw | = | v | | w | 的特殊情形。
--------------------------
几何意义：
点积：
在欧几里得空间中，点积可以直观地定义为
-
,
这里 |x| 表示 x 的范数（长度），θ 表示两个向量之间的角度。
注意：点积的形式定义和这个定义不同；在形式定义中，a 和 b 的夹角是通过上述等式定义的。
这样，两个互相垂直的向量的点积总是零。若 a 和 b 都是单位向量（长度为 1 ），它们的点积就是它们的夹角的余弦。那么，给定两个向量，它们之间的夹角可以通过下列公式得到：
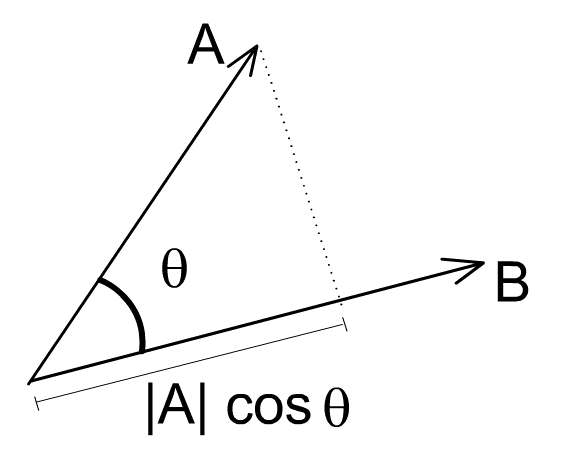
这个运算可以简单地理解为：在点积运算中，第一个向量投影到第二个向量上（这里，向量的顺序是不重要的，点积运算是可交换的），然后通过除以它们的标量长度来“标准化”。这样，这个分数一定是小于等于 1 的，可以简单地转化成一个角度值。
需要注意的是，点积的几何解释通常只适用于 
(
)。在高维空间，其他的域或模中，点积只有一个定义，那就是
点积可以用来计算合力和功。若 b 为单位向量，则点积即为 a 在方向 b 的投影，即给出了力在这个方向上的分解。功即是力和位移的点积。
| A | cos(θ) 是 A 到 B 的投影。
叉积：
