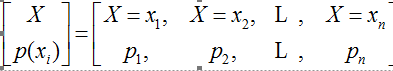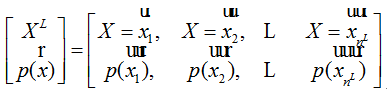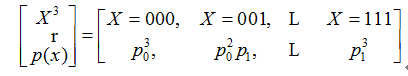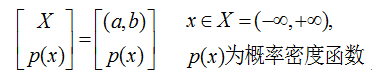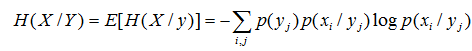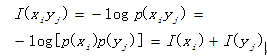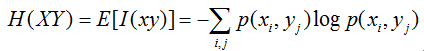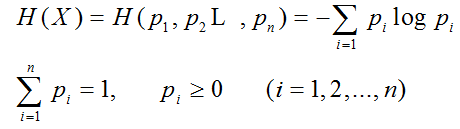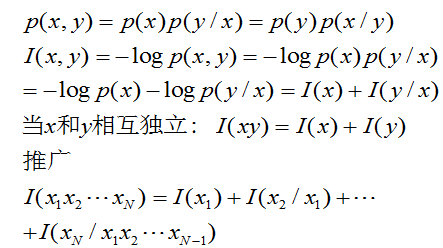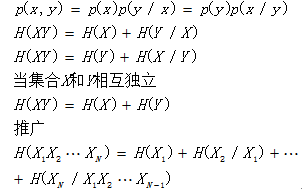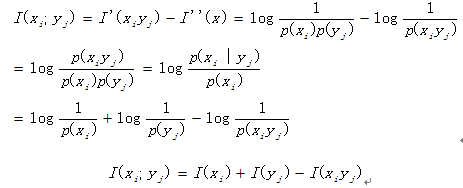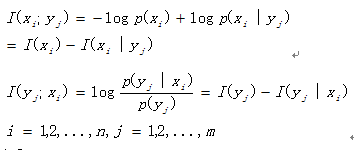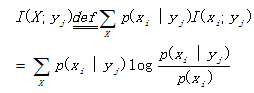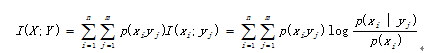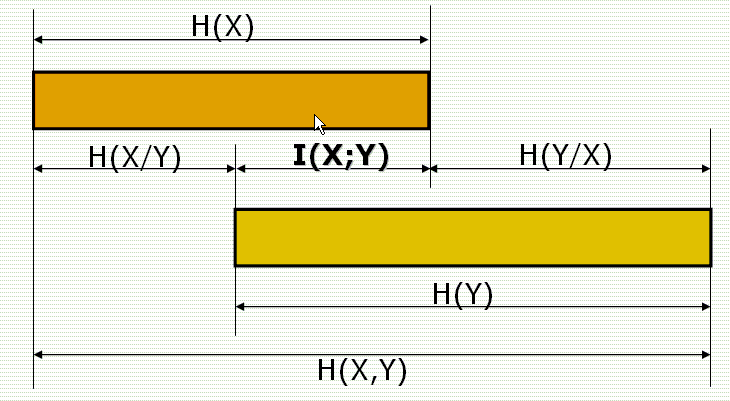第二章-信源与信息熵(一)
主要内容
1. 信源的分类与描述
2. 离散信源的信息熵和互信息
3. 离散序列信源的熵
4. 连续信源的熵与互信息
5. 冗余度
2.1 信源的分类与描述
信源的定义
产生消息(符号)、消息序列和连续消息的来源。
信源的基本特性是具有随机不确定性
l 分类
1. 时间 离散 连续
2. 幅度 离散 连续
3. 记忆 有 无
n 介绍三类信源
Ø 单符号离散信源
Ø 符号序列信源(有记忆和无记忆)
Ø 连续信源
一.单符号离散信源
单符号离散信源:用随机变量X来描述
X的概率空间
二.符号序列信源
离散序列信源:用随机向量XL描述
以3位PCM信源为例
三.连续信源
连续信源:用随机过程x(t)描述
px(x)不再是概率分布,而是概率密度分布函数
2.2 离散信源熵与互信息
信息量
自信息→平均自信息→符号熵
联合自信息→平均联合自信息→联合熵
条件自信息量→平均条件自信息→条件熵
单符号离散信源熵
符号熵
条件熵
联合熵
一.自信息量
1. 定义
对于给定的离散概率空间表示的信源,x=xi事件所对应的(自)信息为
I(xi) = - logp(xi)
以2为底,单位为比特(bit)
以e为底,单位为奈特(nat)
1nat=1.433bit
以10为底,单位为笛特(det)
1det=3.322bit
2. 性质
u 两种特殊情况
l p(xi)=1,确定事件,信息量I(xi)=0
l p(xi)=0 ,I(xi)=无穷,概率为0的事件带来极大的信息量
u I(xi) ≥0,非负性
u I(xi)是p(xi)的单调递减函数
u xi是一个随机量, I(xi)是xi的函数,也是随机变量,没有确定的值
Question?
自信息量I(xi)能反映整个信源的不确定性吗?
如果不能,那用什么量来反映呢?
3. 平均自信息量——信息熵H(X)
Answer:
用自信息量的平均值来描述
算术平均值
数学期望:加权平均值
1. 定义——信息熵
对于给定离散概率空间表示的信源所定义的随机变量I(xi)的数学期望(加权平均值)
2. 熵的物理含义
H(X)表示信源发出任何一个消息状态所携带的平均信息量
也等于在无噪声条件下,接收者收到一个消息状态所获得的平均信息量
熵的本意为热力学中表示分子状态的紊乱程度
信息论中熵表示信源中消息状态的不确定度
信源熵与信息量有不同的意义:
l H(X)表示信源X每一个状态所能提供的平均信息量
l H(X)表示信源X在没有发出符号以前,接收者对信源的平均不确定度
l H(X)表示随机变量X的随机性
二.条件自信息
联合集XY中,在事件yj发生的条件下,关于事件xi的条件(自)信息量为:
I(xi/yi) = - logp(xi/yi)
平均条件自信息量——条件熵
定义:
联合集XY上,条件自信息量I(xi/yj)的概率加权平均值
如何求平均?
先在X集合上求平均(此时,在yj事件发生的条件下)
再在Y集合上求平均
三.联合自信息
1.定义:
联合概率空间中任一联合事件的联合(自)信息量为:
I(xi,yi) = - logp(xi,yi)
当X和Y相互独立时,
2. 联合熵
联合集XY上,每对事件的自信息量的概率加权平均值定义为联合熵。
单位为比特/序列
将联合事件xiyj作为一个随机事件求平均不确定度
四.熵函数的性质
熵函数可表示为
- 非负性 H(X) ≥0
- 对称性
概率矢量中的各分量的次序任意变更时,熵值不变
- 确定性
信源概率空间中,任意一个概率分量等于1,其它概率分量必为0
信源为确知信源,其熵为0
- 连续性
- 扩展性
- 最大熵定理
条件熵小于无条件熵
![]()
推广:多条件熵小于少条件熵
- 条件熵小于无条件熵
五.几种自信息量之间的关系
自信息量、联合自信息量、条件自信息量都满足非负性和单调递减性。
三者都是随机变量,其值随着变量xi和yj的变化而变化。
关系式:
![]()
六.几种熵之间的关系
小结:
一共介绍了
自信息量ß---->平均自信息量
联合自信息量ß---->联合熵
条件自信息量ß---->条件熵
引入另一个很重要的概念——互信息
涉及到信息的交互
七.互信息
1.定义
接收端收到集合Y 中的一个消息符号yj后,重新估计关于信源的各个消息xi发生的概率,为条件概率p(xi / yj),即后验概率。
互信息量=不确定程度的减少量
通信前
将信道看成关闭,可以认为输入随机变量X和输出随机变量Y之间没有任何关联关系,即X、Y统计独立。根据概率的性质,输入端出现xi和输出端出现yj的概率为:
![]()
此时,先验不确定度为
通信后
输入随机变量X和输出随机变量Y之间由信道的统计特性相联系。输入端出现xi和输出端出现yj的联合概率为
此时,后验不确定为
则,通信后流经信道的信息量等于通信前后不确定度的差,即yj带来关于xi的信息量:
互信息量定义为自信息量减去条件自信息量的差:
2.性质
1) 互易性:I(x;y) = I(y;x)
2) 互信息量可为0
3) 可正可负
4) 任何两个事件之间的互信息量小于其中任一事件的自信息量
3.平均互信息
联合集XY上求加权平均和
先在X集合上求平均
再在Y集合上求权平均值
综合一下,平均互信息量
在联合概率空间P(XY)中的统计平均值
4.平均互信息的性质
u 非负性:I(X;Y) ≥ 0
u 互易性:I(X;Y) =I(Y;X)
u 与熵和条件熵及联合熵关系
I(X;Y) = H(X) – H(X/Y) = H(Y) – H(Y/X) = H(X) + H(Y) –H(XY)
u 极值性
互信息量总是小于等于自信息量
接收者收到的信息量不可能大于信源发出的信息量
只有当信道为无噪声信道时,接收信息量才等于信源发出的信息量。
u 凸性函数性质
l 上凸性
n 当条件概率p(yj/xi)给定时,平均互信息量I(X;Y)是信源概率分布p(xi)的∩型上凸函数
n 极大值
n 信道容量C:对于给定的信道,总可以找到一个先验概率分布为pm(xi)的信源,使得平均互信息量达到最大值
n 这个信源为该信道的匹配信源
l 下凸性
n 当信源X的概率分布p(xi)保持不变时,平均互信息量I(X;Y)是条件概率分布p(yj/xi)的∪型下凸函数
n 极小值
n 信息率失真函数R(D)
u 信息不增性原理
l I(X,Y;Z)=I(X;Z)+I(Y;Z/X)
l I(X,Y;Z)=I(Y;Z)+I(X;Z/Y)
l 则有:I(X;Z)=I(Y;Z)+I(X;Z/Y)-I(Y;Z/X)
l 假设在Y条件下X与Z相互独立
n 即I(X;Z/Y)=0,且I(X;Y/Z)和I(Y;Z/X)均非负
n 则有:I(X;Z)≤I(Y;Z) I(X;Z)≤I(X;Y)
l I(X;Z)≤I(Y;Z) I(X;Z)≤I(X;Y)
l 含义
n 当消息经过多级处理时,随着处理级数的增多,输入消息和输出消息之间的平均互信息量趋于变小。
l 数据处理定理
n 数据的处理过程中只会失掉一些信息,绝不会创造出新的信息
n 信息不增性
Ø 疑义度
n I(X,Y)=H(X)-H(X/Y)
n 表示接收者收到Y后,对信源X仍然存在的平均不确定度
n 对于接收者来说,H(X)称为先验不确定度,H(X/Y)称为后验不确定度。
n 平均交互信息量等于不确定度的变化量
Ø 噪声熵
n 扩散度,噪声熵
n I(X,Y)=H(Y)-H(Y/X)
n 表示发信者发出X后,对信道输出Y仍然存在的平均不确定度
n 对于发信者来说,H(Y)称为先验不确定度,H(Y/X)称为后验不确定度。
n 平均交互信息量等于不确定度的变化量
Ø 联合熵(共熵)
l I(X,Y)=H(X)+H(Y)-H(X,Y)
l 表示通信完成之后,观察者对通信系统仍然存在的平均不确定度
l 对于观察来说
n H(X)+H(Y)称为先验不确定度
n H(X,Y)称为后验不确定度
l 平均交互信息量等于不确定度的变化量
l I(X,Y)=H(X)-H(X/Y)=H(Y)-H(Y/X)=H(X)+H(Y)-H(X,Y)