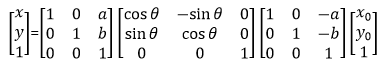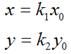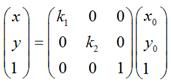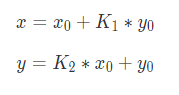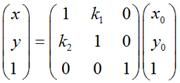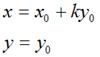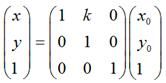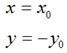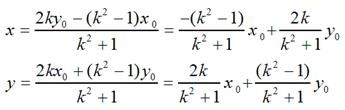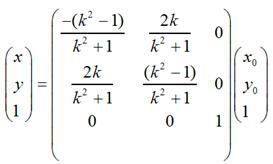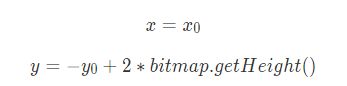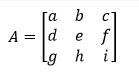Android变形矩阵——Matrix

既然要讲Android中的矩阵肯定少不了变形矩阵Matrix。上篇博文我们介绍了色彩矩阵，那是用于图像色彩处理的。而变形矩阵是用于图形变换的。

图像的变形主要有以下五种基本类型：
- 平移变换
- 旋转变换
- 缩放变换
- 错切变换
- 对称变换

变形矩阵基础

在讲解如何变换之前，先介绍以下变形矩阵。

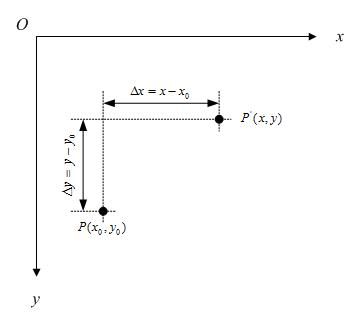
对于一张图片，它的每一个像素点都会有相应的x、y坐标。而图形变换就是将图片的每一个像素点的xy坐标通过变形矩阵去处理，从而达到图形变换的效果。

Android的图形变换矩阵是一个3*3的矩阵：

其中矩阵A就是变形矩阵，C中的XY代表的是原图片中的像素点坐标，R中的X1Y1代表变换后的坐标。

通过矩阵乘法可知：

X_1=a*X+b*Y+c

Y_1=d*X+e*Y+f

1=g*X+h*Y+i

与色彩矩阵一样，图形变换矩阵同样有一个初始矩阵：

当与初始矩阵相乘是不会产生任何图形变换的。

---

现在来讲下Android代码如何使用图形变换矩阵：

我们通过如下代码来初始化一个变形矩阵：

        Matrix matrix = new Matrix();

这时候生成的矩阵就是初始矩阵。

图形变换矩阵也是可以通过一维数组存储：

[ a, b, c, d, e,f, g, h, i ]

我们可以通过如下方法来设置我们需要的矩阵：

matrix.setValues(new float[]{
                1, 0, 300,
                0, 1, 500,
                0, 0, 1,
        });

设置好矩阵之后就是应用到bitmap上了，有如下两种常用方法：

第一种是canvas的：

canvas.drawBitmap(bitmap, matrix, mPaint);

第二种是ImageView的：

setImageMatrix(matrix); 

基础就讲到这里，下面就开始讲图形变换吧：

图形变换

为了更好的讲解，我们结合一个简单的demo。该demo是一个简单的自定义view，显示了一张正方形图片而已：

代码如下：

public class MyMatrix extends View {

    private Paint mPaint;// 画笔
    private Bitmap bitmap;// 位图
    Matrix matrix;

    public MyMatrix(Context context) {
        this(context, null);
    }

    public MyMatrix(Context context, AttributeSet attrs) {
        super(context, attrs);

        mPaint = new Paint(Paint.ANTI_ALIAS_FLAG);

        bitmap = BitmapFactory.decodeResource(context.getResources(), R.drawable.p2);

    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        // 绘制位图
        canvas.drawBitmap(bitmap, 0, 0, mPaint);
    }
}

好了，下面开始进入正题：

1、平移变换

平移变换即将图像每个像素点都进行平移变换。

当一个点从平移到
时，其x轴和y轴方向移动的大小为：

如下图所示：（Android中的坐标系以屏幕左上角为坐标原点）

不难知道：

写成矩阵的话就是：

这个矩阵也就是平移变换矩阵。

现在结合我们的demo来演示一下：

public class MyMatrix extends View {

    private Paint mPaint;// 画笔
    private Bitmap bitmap;// 位图
    Matrix matrix;

    public MyMatrix(Context context) {
        this(context, null);
    }

    public MyMatrix(Context context, AttributeSet attrs) {
        super(context, attrs);

        mPaint = new Paint(Paint.ANTI_ALIAS_FLAG);

        bitmap = BitmapFactory.decodeResource(context.getResources(), R.drawable.p2);

        //设置矩阵
        matrix = new Matrix();
        matrix.setValues(new float[]{
                1, 0, 200,
                0, 1, 50,
                0, 0, 1,
        });

    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        // 绘制位图
        canvas.drawBitmap(bitmap, 0, 0, mPaint);
        //绘制套用矩阵后的位图
        canvas.drawBitmap(bitmap, matrix, mPaint);
    }
}

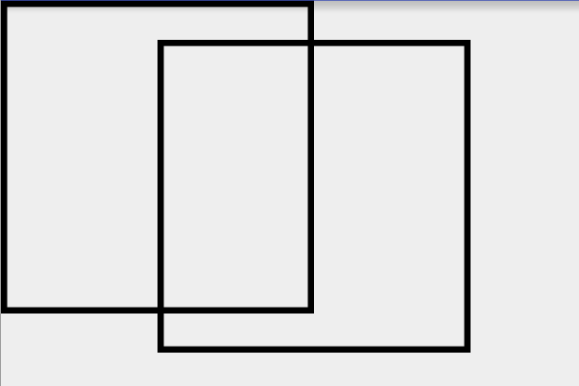
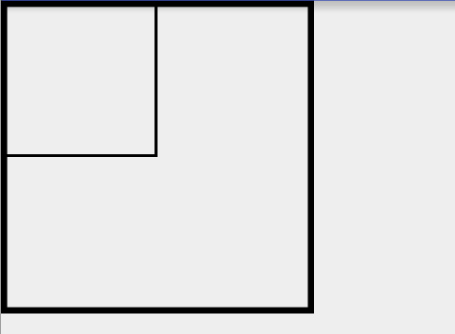
我就在上面的demo上加上变形矩阵，这个矩阵使原图向x轴正向位移200，y轴正向位移50，然后在绘制了普通的方框之后又绘制了一次套用了矩阵的方框。效果如下：

2、旋转变换

旋转变换即指一个点围绕一个中心旋转到一个新的点。

旋转变换有两种：
1. 直接绕坐标原点[0,0]旋转
2. 指定中点，也就是将坐标原点[0,0]平移后在旋转

（1）围绕坐标原点旋转：

当从点，以坐标原点为旋转中心旋转到点时，假定P点离坐标原点的距离为r，如下图：

通过三角函数，我们可以得出以下公式：

用矩阵表示为：

（2）围绕某个点旋转

围绕某一点O进行旋转变换，可以分成3个步骤：
1. 将坐标原点平移到O点
2. 围绕新的坐标原点O进行旋转变换
3. 将坐标原点移回到原先的坐标原点。

用矩阵表示即为：

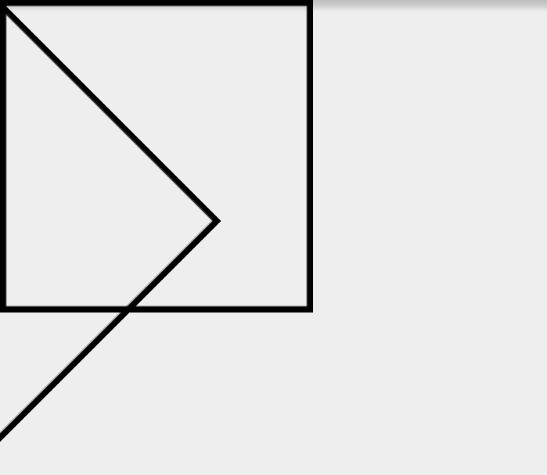
至于用矩阵来进行旋转真的太反人类了，谷歌肯定帮我们封装好了相应的方法，后面我会一起讲解，现在只展示旋转45度之后的demo的效果：

可以发现正方形围绕这坐标原点旋转了45度。

3、缩放变换

一个像素点是不存在缩放的概念的，但是由于图像是由很多个像素点组成，如果将每个点的坐标都进行相同比例的缩放，最终就会形成让整个图像缩放的效果。即：

矩阵形式：

将我们demo的矩阵换成如下形式：

 matrix.setValues(new float[]{
                0.5F, 0, 0,
                0, 0.5F, 0,
                0, 0, 1,
        });

即可将x，y轴方向都缩放为原来的0.5倍，效果如下：

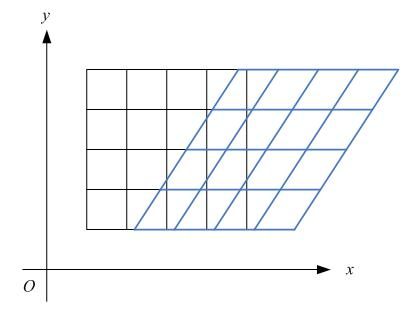
4、错切变换

错切变换(skew)在数学上又称为Shear mapping(可译为“剪切变换”)或者Transvection(缩并)，它是一种比较特殊的线性变换。错切变换的效果就是让所有点的x坐标(或者y坐标)保持不变，而对应的y坐标(或者x坐标)则按比例发生平移，且平移的大小和该点到x轴(或y轴)的垂直距离成正比。

错切变换，属于等面积变换，即一个形状在错切变换的前后，其面积是相等的。

错切包含两种：

1. 水平错切：各点的y坐标保持不变，但其x坐标则按比例发生了平移。

   

2. 垂直错切：各点的x坐标保持不变，但其y坐标则按比例发生了平移。

   

假定一个点经过错切变换后得到，则

错切变换的计算公式如下：

写成矩阵形式则如下：

其中，对于水平错切，有如下关系：

矩阵形式为：

同理，垂直错切的矩阵形式为：

现在我们结合demo演示一下错切的效果，为了方便显示错切的效果，我将原本的方框换成了有方格的正方形：

矩阵如下：

matrix.setValues(new float[]{
                1, 1, 0,
                0, 1, 0,
                0, 0, 1,
        });

是一个非常简单的水平

效果如下：

通过之前的公式，可以发现就是demo中演示的效果

5、对称变换

所谓对称变换，就是经过变化后的图像和原图像是关于某个对称轴是对称的。

比如某点对称变换得到。

• 若对称轴是x轴，则：

  

  矩阵表示为：

  

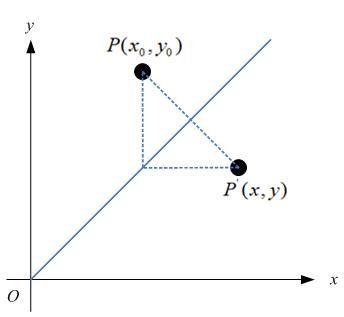
• 若对称轴为y=x，如图：

  

  那么可以得出以下关系：

  

  解得：

  

  矩阵表示为：

  

• 若对称轴是y = kx

  

  那么：

  

  解得：

  

  矩阵表示为：

  

• 若对称轴是y = kx + b

  对于这种情况，只需要在上面的基础上增加两次平移变换即可，即先将坐标原点移动到(0, b)，然后做上面的关于y = kx的对称变换，再然后将坐标原点移回到原来的坐标原点即可。用矩阵表示大致是这样的：

  

其实大致的思路就是通过列方程找出两个点坐标的关系，然后套用到矩阵上

注意：

我们Android的坐标系是以屏幕左上角为坐标原点，所以屏幕的y坐标的正向和数学中y坐标的正向刚好是相反的，上面是以数学中常用的坐标系计算的，所以在实际开发中记得转换

现在结合demo来演示一下：

效果如下：

这里我以图片的高度位置，即y=bitmap.getHeight()为对称轴，做了对称变换

通过简单的运算可以得出一下关系式：

所以使用的矩阵为：

 matrix.setValues(new float[]{
                1, 0, 0,
                0, -1, 2*bitmap.getHeight(),
                0, 0, 1,
        });

之后就是如图所示的效果

总结

对于矩阵：

可以发现a、b、c、d、e、f分别对应一下变换：
- a和e对应控制Scale——缩放变换
- b和d对应控制Skew——错切变换
- c和f对应控制Translate——平移变换
- a、b、d、e共同控制Rotate——旋转变换

相应的Android API

对于上面的变换，Android都相应的提供了Api

大致如下：

• 旋转变换

matrix.setRotate();

• 平移变换

matrix.setTranslate();

• 缩放变换

matrix.setScale();

• 错切变换

matrix.setSkew();

其中还有preXXX()和postXXX()方法，分别对应这前乘和后乘。

Matrix的setXXX()方法会重置矩阵中的所有值，而preXXX()和postXXX()方法则不会。

结合一个demo来说明一下：

对于我们方形的那个demo，我们对其进行如下矩阵变换：

matrix.setRotate(45);
matrix.postTranslate(bitmap.getWidth(),0);
matrix.postTranslate(0,bitmap.getHeight());

其中，我先以原点旋转了45度，然后再向右平移了这个矩阵的宽度，最后再向下平移了这个矩阵的高度，所以效果如下：

若我换成：

matrix.postTranslate(bitmap.getWidth(),0);
matrix.setRotate(45);
matrix.postTranslate(0,bitmap.getHeight());

将set放在了post之后，那么就会像之前所说的，我们第一次的矩阵变换：
matrix.postTranslate(bitmap.getWidth(),0);就会失效，所以最后结果就会少了向右平移的操作：

如果结合pre操作：

matrix.setTranslate(bitmap.getWidth(),0);
matrix.preRotate(45);
matrix.postTranslate(0,bitmap.getHeight());

这个效果则与之前的第一次操作效果相同：

matrix.setRotate(45);
matrix.postTranslate(bitmap.getWidth(),0);
matrix.postTranslate(0,bitmap.getHeight());

本文参考
《Android群英传》
Android Matrix