IMU比较详细的内容(主要是针对卡尔曼滤波器)(摘自于ipythonnotebook)

IMU比较详细的内容(主要是针对卡尔曼滤波器)(摘自于ipythonnotebook)

C++代码，编的比较好，可以仿照。下面是对他的资料的整理。

• 代码均是基于面向对象设计的，调用函数后发现参数输入太少了吧
  • 运行后发现结果不对
  • 对于GPS的模块的调用显得很复杂，最后给位置算积分也不太对
    实际上是仿照这个代码 Kalman-master ，内容主要包含下面两张图：
    
    The coordinate system is as in DIN70000:
    
    非常重要：横滚（roll）(fai)和俯仰（pitch）(seta)摇头（yaw）(psi)
    单位如下：

	The units are:
			Lat/Lon in decimal degree (from GPS)
			speed in km/h (from GPS)
			course in degree (from GPS)
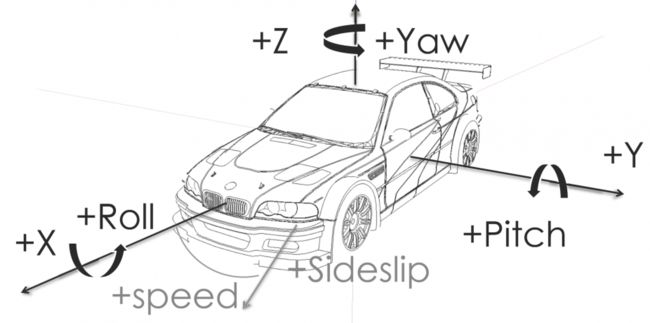
			roll/pitch/yaw in degree (from IMU)
			roll-/pitch-/yawrate in degrees/second (from IMU)
			acclerations in m/s² (from IMU)

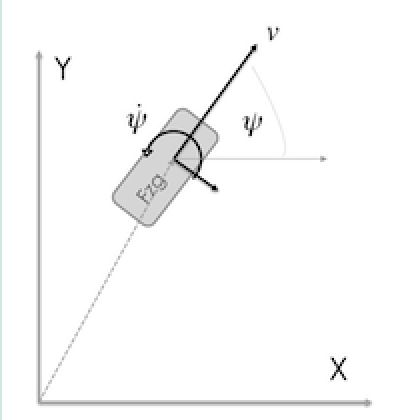
该开源项目主要是针对“汽车”而言，所以很多情况下是一个二维的系统，只有xy两个方向。为此，首先的简化如下：

1. 恒定速度行驶，汽车过隧道
   这里阐述了相应矩阵的确定：

		P： 初始化不确定性
		R： 观测误差协方差
		Q： 过程噪声协方差(类似于风的印象，加速度的干扰)

$$P_0=\left[\begin{array}{cccc}{\sigma }_x^2& 0& 0& 0\\ 0& {\sigma }_y^2& 0& 0\\ 0& 0& {\sigma }_x^2& 0\\ 0& 0& 0& {\sigma }_y^2\end{array}\right]$$

$$R=\left[\begin{array}{cc}{\sigma }_{\dot{x}}^2& 0\\ 0& {\sigma }_{\dot{y}}^2\end{array}\right]$$
过程噪声协方差比较复杂：
$$Q=\left[\begin{array}{cccc}{\sigma }_x^2& {\sigma }_{xy}& {\sigma }_{xx}& {\sigma }_{xy}\\ {\sigma }_{yx}& {\sigma }_y^2& {\sigma }_{y\dot{x}}& {\sigma }_{y\dot{y}}\\ {\sigma }_{xx}& {\sigma }_{xy}& {\sigma }_x^2& {\sigma }_{x\dot{y}}\\ {\sigma }_{yx}& {\sigma }_{yy}& {\sigma }_{yx}& {\sigma }_y^2\end{array}\right]$$
有如下：
$$Q=G\cdot G^T\cdot {\sigma }_v^2$$
其中，
$$G={\left[\begin{array}{llll}0.5d{t}^2& 0.5d{t}^2& dt& dt\end{array}\right]}^T$$
代码如下：

sa = 0.1
G = np.matrix([[1/2.0*dt**2],
               [1/2.0*dt**2],
               [dt],
               [dt],
               [1.0],
               [1.0]])
Q = G*G.T*sa**2
print(Q, Q.shape)

但是有如下结果，是不是代表已经发散了？

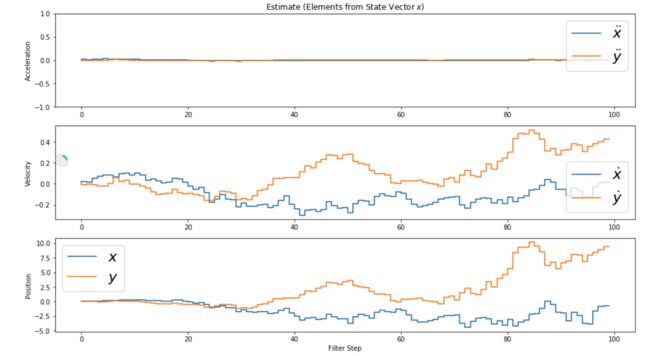
事实证明已经发散了。因为这里观测的是加速度，但是位置的初始误差是很难估计出来的。
2. 球在三维中运动，观测球的位置
模拟球的运动：

Hz = 100.0 # Frequency of Vision System
dt = 1.0/Hz
T = 1.0 # s measuremnt time
m = int(T/dt) # number of measurements

px= 0.0 # x Position Start
py= 0.0 # y Position Start
pz= 1.0 # z Position Start

vx = 10.0 # m/s Velocity at the beginning
vy = 0.0 # m/s Velocity
vz = 0.0 # m/s Velocity

c = 0.1 # Drag Resistance Coefficient阻力阻力系数
d = 0.9 # Damping阻尼

Xr=[]
Yr=[]
Zr=[]
for i in range(int(m)):
    accx = -c*vx**2  # Drag Resistance
    
    vx += accx*dt
    px += vx*dt

    accz = -9.806 + c*vz**2 # Gravitation + Drag
    vz += accz*dt
    pz += vz*dt
    
    if pz<0.01:
        vz=-vz*d
        pz+=0.02
    if vx<0.1:
        accx=0.0
        accz=0.0
        
    Xr.append(px)
    Yr.append(py)
    Zr.append(pz)
# 模拟球的运动

估计位置距离球的位置0.25m。
卡尔曼滤波器仅用于线性动态系统。阻力系数在某种状态下是非线性的，但是滤波器可以处理该阻力，直到达到一定程度的阻力为止。但是这时，球撞到了地面，非线性度过高，滤波器提供了错误的解决方案。因此，必须在滤波器环路中对开关进行建模，这有助于滤波器获得它。
下面给出了离散的动力学模型：
$$x_{k+1}=\left[\begin{array}{ccccccccc}1& 0& 0& \Delta t& 0& 0& \frac{1}{2}\Delta t^2& 0& 0\\ 0& 1& 0& 0& \Delta t& 0& 0& \frac{1}{2}\Delta t^2& 0\\ 0& 0& 1& 0& 0& \Delta t& 0& 0& \Delta t^2\\ 0& 0& 0& 1& 0& 0& \Delta t& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& \Delta t& 0\\ 0& 0& 0& 0& 0& 1& 0& 0& \Delta t\\ 0& 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]x_k$$
这里同样结果很糟糕
3. 观测位置与加速度
结果不错。
4. 这里涉及到加速度计与陀螺仪之间的关系估算角度，观测是用加速度计和陀螺仪
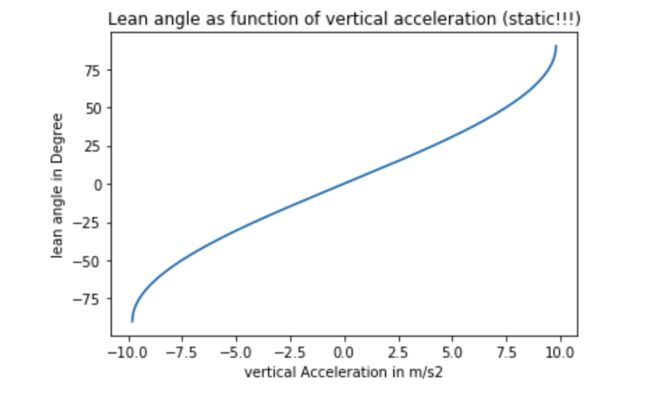
转速传感器直接测量，加速度传感器直接测量重力，因此不直接测量倾斜角ф。倾斜角和由加速度传感器测量的垂直加速度a之间存在数学联系。它是余弦。如果自行车直立，则加速度a恰好为1g，如果ф= 90°，则加速度为0g。
$a=g\cdot \cos \left(90^{\circ }-\varphi \right)$
有如下关系：
![]

page2 扩展卡尔曼滤波

概括如下：
$${\tilde{P}}_k=F_{k-1}{\hat{P}}_{k-1}{F}_{k-1}^T+Q_k^{\prime }$$
$${\tilde{x}}_k=f\left({\hat{x}}_{k-1},v_k,0\right)$$
$$K_k={\tilde{P}}_k{G}_k^T{\left(G_k{\tilde{P}}_k{G}_k^T+R_k^{\prime }\right)}^{-1}$$
$${\hat{P}}_k=\left(I-K_k{G}_k\right){\tilde{P}}_k$$ ,
$${\hat{x}}_k={\tilde{x}}_k+K_k\left(y_k-g\left({\tilde{x}}_k,0\right)\right)$$
其中，
$F_{k-1}={\frac{\partial f}{\partial x_{k-1}}|}_{{\hat{x}}_{k-1}},G_k={\frac{\partial h}{\partial x_k}|}_{{\tilde{x}}_k}$
故而，下面整理了kalman滤波的普遍做法：

Labbe

$$\begin{array}{rl}\overline{\mathbf{x}}& =\mathbf{F}\mathbf{x}+\mathbf{B}\mathbf{u}\\ \overline{\mathbf{P}}& ={\mathbf{F}\mathbf{P}\mathbf{F}}^{\mathsf{T}}+\mathbf{Q}\\ & \\ \mathbf{y}& =\mathbf{z}-\mathbf{H}\overline{\mathbf{x}}\\ \mathbf{S}& =\mathbf{H}\overline{\mathbf{P}}{\mathbf{H}}^{\mathsf{T}}+\mathbf{R}\\ \mathbf{K}& =\overline{\mathbf{P}}{\mathbf{H}}^{\mathsf{T}}{\mathbf{S}}^{-1}\\ \mathbf{x}& =\overline{\mathbf{x}}+\mathbf{K}\mathbf{y}\\ \mathbf{P}& =(\mathbf{I}-\mathbf{K}\mathbf{H})\overline{\mathbf{P}}\end{array}$$

Wikipedia

$$\begin{array}{rl}{\hat{\mathbf{x}}}_{k\mid k-1}& ={\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1\mid k-1}+{\mathbf{B}}_k{\mathbf{u}}_k\\ {\mathbf{P}}_{k\mid k-1}& ={\mathbf{F}}_k{\mathbf{P}}_{k-1\mid k-1}{\mathbf{F}}_k^{\text{T}}+{\mathbf{Q}}_k\\ {\tilde{\mathbf{y}}}_k& ={\mathbf{z}}_k-{\mathbf{H}}_k{\hat{\mathbf{x}}}_{k\mid k-1}\\ {\mathbf{S}}_k& ={\mathbf{H}}_k{\mathbf{P}}_{k\mid k-1}{\mathbf{H}}_k^{\text{T}}+{\mathbf{R}}_k\\ {\mathbf{K}}_k& ={\mathbf{P}}_{k\mid k-1}{\mathbf{H}}_k^{\text{T}}{\mathbf{S}}_k^{-1}\\ {\hat{\mathbf{x}}}_{k\mid k}& ={\hat{\mathbf{x}}}_{k\mid k-1}+{\mathbf{K}}_k{\tilde{\mathbf{y}}}_k\\ {\mathbf{P}}_{k|k}& =(I-{\mathbf{K}}_k{\mathbf{H}}_k){\mathbf{P}}_{k|k-1}\end{array}$$

Brookner

$$\begin{array}{rl}{X}_{n+1,n}^{\ast }& =\Phi X_{n,n}^{\ast }\\ X_{n,n}^{\ast }& =X_{n,n-1}^{\ast }+H_n(Y_n-M{X}_{n,n-1}^{\ast })\\ H_n& =S_{n,n-1}^{\ast }{M}^{\mathsf{T}}[R_n+M{S}_{n,n-1}^{\ast }{M}^{\mathsf{T}}{]}^{-1}\\ S_{n,n-1}^{\ast }& =\Phi S_{n-1,n-1}^{\ast }{\Phi }^{\mathsf{T}}+Q_n\\ S_{n-1,n-1}^{\ast }& =(I-H_{n-1}M)S_{n-1,n-2}^{\ast }\end{array}$$

Gelb

$$\begin{array}{rl}{\underline{\hat{x}}}_k(-)& ={\Phi }_{k-1}{\underline{\hat{x}}}_{k-1}(+)\\ {\underline{\hat{x}}}_k(+)& ={\underline{\hat{x}}}_k(-)+K_k[Z_k-H_k{\underline{\hat{x}}}_k(-)]\\ K_k& =P_k(-)H_k^{\mathsf{T}}[H_k{P}_k(-)H_k^{\mathsf{T}}+R_k{]}^{-1}\\ P_k(+)& ={\Phi }_{k-1}{P}_{k-1}(+){\Phi }_{k-1}^{\mathsf{T}}+Q_{k-1}\\ P_k(-)& =(I-K_k{H}_k)P_k(-)\end{array}$$

Brown

$$\begin{array}{rl}{\hat{\mathbf{x}}}_{k+1}^{-}& ={\varphi }_k{\hat{\mathbf{x}}}_k\\ {\hat{\mathbf{x}}}_k& ={\hat{\mathbf{x}}}_k^{-}+{\mathbf{K}}_k[{\mathbf{z}}_k-{\mathbf{H}}_k{\hat{x}}_k^{-}]\\ {\mathbf{K}}_k& ={\mathbf{P}}_k^{-}{\mathbf{H}}_k^{\mathsf{T}}[{\mathbf{H}}_k{\mathbf{P}}_k^{-}{\mathbf{H}}_k^T+{\mathbf{R}}_k{]}^{-1}\\ {\mathbf{P}}_{k+1}^{-}& ={\varphi }_k{\mathbf{P}}_k{\varphi }_k^{\mathsf{T}}+{\mathbf{Q}}_k\\ {\mathbf{P}}_k& =(\mathbf{I}-{\mathbf{K}}_k{\mathbf{H}}_k){\mathbf{P}}_k^{-}\end{array}$$

Zarcha

$$\begin{array}{rl}{\hat{x}}_k& ={\Phi }_k{\hat{x}}_{k-1}+G_k{u}_{k-1}+K_k[z_k-H{\Phi }_k{\hat{x}}_{k-1}-H{G}_k{u}_{k-1}]\\ M_k& ={\Phi }_k{P}_{k-1}{\varphi }_k^{\mathsf{T}}+Q_k\\ K_k& =M_k{H}^{\mathsf{T}}[H{M}_k{H}^{\mathsf{T}}+R_k{]}^{-1}\\ P_k& =(I-K_{k}H)M_k\end{array}$$
或者也可以表示如下：
![]