IMU噪声参数辨识-艾伦方差

前言

在统计学中描述随机变量的两个经典参数是均值和方差，早期在定量表征原子钟的频率稳定度时采用的就是经典方差方法。1996年，学者D.W.Allan在分析铯原子钟频标的频率稳定度时发现经典方差随着时间的增长而发散，为了解决该问题，提出了一种新的评定方法，后来称为艾伦方差。由于惯性器件也具有振荡器的特征，Allan方差分析也被广泛应用于惯性器件的随机误差建模，IEEE标准中就将Allan方差方法引入到了激光陀螺的建模分析。
Allan方差的物理意义以及应用本质来源于它与功率谱之间的关系，本文首先从功率谱入手推导艾伦方差，然后教大家如何从艾伦方差log曲线中辨识IMU的各种噪声，最后会给出Allan方差的实例应用，包括光纤惯导和Mems惯导，并且给出了和10s平滑方法的差异。

推导过程

因为内容较多，这里只会给出一个大概的推导流程，更多细节的推导可以参考严恭敏老师《惯性仪器测试与数据分析》一书。
从时域测量方面来分析，Allan方差定义如下:
$${\sigma }_y^2(\tau )=\frac{1}{2}<{\left[y_{i+1}(\tau )-y_i(\tau )\right]}^2>$$
然后是艾伦方差和功率谱密度之间的关系，如下所示：
$${\sigma }_y^2(\tau )=2{\int }_{-\infty }^{\infty }{S}_y(f)\frac{{\sin }^4(\pi f\tau )}{(\pi f\tau {)}^2}\mathrm{d}f=4{\int }_0^{\infty }{S}_y(f)\frac{{\sin }^4(\pi f\tau )}{(\pi f\tau {)}^2}\mathrm{d}f$$
上式中$S_y(f)$为功率谱密度。
从艾伦方差曲线中可以辨识出IMU的五种噪声，分别为：量化噪声、角度随机游走、零偏不稳定性噪声，角速率随机游走，速率斜坡，一般在IMU噪声辨识中用的比较多的是中间3种。
下面分别介绍5种噪声和Allan方差之间的关系。

1. 量化噪声（Quantization Noise，QN）

量化噪声产生的来源是传感器在经过A/D转换环节，即存在模拟量向数字量的转化的量化过程，然后这一过程是必然存在信息损失的，所以量化噪声代表了传感器检测的最小分辨率水平。
角速率的量化噪声功率谱为：
$$S_{\Omega }(f)={\tau }_0{Q}^2(2\pi f{)}^2$$
代入艾伦方差和功率谱密度关系公式中得到：
$${\sigma }_{QN}^2(\tau )=4{\int }_0^{\infty }{\tau }_0{Q}^2(2\pi f{)}^2\frac{{\sin }^4(\pi f\tau )}{(\pi f\tau {)}^2}\mathrm{d}f=\frac{16{\tau }_0{Q}^2}{\pi {\tau }^3}{\int }_0^{\infty }{\sin }^4(\pi f\tau )\mathrm{d}(\pi f\tau )$$
上公式化简整理可得：
$${\log }_{10}{\sigma }_{QN}(\tau )={\log }_{10}\sqrt{3}Q-{\log }_{10}\tau$$
由此可见，在Allan方差$\tau -{\sigma }_{QN}$双对数图上，量化噪声对应的斜率为-1，它（或延长线）与$\tau =1$交点的纵坐标读数为$\sqrt{3}Q$，如下图所示。

这里需要注意一下，严格意义上应该称$\sigma (\tau )$为Allan标准差，而称$\sigma (\tau {)}^2$为Allan方差，但习惯上常常直接称$\sigma (\tau )$为Allan方差，以后在不引起歧义的情况下所说的Allan方差亦指$\sigma (\tau )$，在概念上不要造成混乱。
量化噪声具有很宽的带宽，属于高频噪声，在实际应用中可进行低通滤波处理或大部分被导航姿态更新（积分）环节所滤除，因而一般对系统精度的影响不大。

2．角度随机游走（Angular Random Walk，ARW）

如果陀螺仪角速度为高斯白噪声，那么积分得到的角度就会表现为角度随机游走现象。根据随机过程理论，随机游走是一种独立增量过程，含义是：角速率白噪声在两相邻采样时刻进行积分，不同时段的积分值之间互不相关。
从角速率来看，其功率谱为常值，公式如下：
$$S_{\Omega }(f)=N^2$$
公式中的N为角度随机游走系数，同样的，代入艾伦方差和功率谱密度关系公式中可得：
$${\sigma }_{ARW}^2(\tau )=4{\int }_0^{\infty }{N}^2\frac{{\sin }^4(\pi f\tau )}{(\pi f\tau {)}^2}\mathrm{d}f=\frac{4N^2}{\pi \tau }{\int }_0^{\infty }\frac{{\sin }^4(\pi f\tau )}{(\pi f\tau {)}^2}\mathrm{d}(\pi f\tau )=\frac{N^2}{\tau }$$
可见，在$\tau -{\sigma }_{ARW}(\tau )$，角度随机游走的斜率为$-1/2$，它（或延长线）与 $\tau =1$的交点纵坐标读数即为角度随机游走系数$N$，如下图所示。

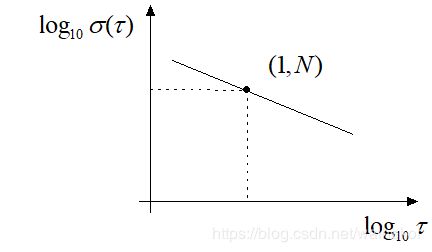
角度随机游走是陀螺仪非常重要的一个噪声参数，在卡尔曼滤波中设置P阵中需要辨识这一参数。如果使用的是陀螺仪角增量信号，因为增量输出是一个积分过程，所以Allan方差的角度随机游走系数和采样频率无关，但是如果直接采样角速率数据，建议尽量提高采样频率来减少信息的损失，比如取两倍的带宽频率，能达到4到6倍或者以上更佳。

3．零偏不稳定性噪声（Bias Instability，BI）

根据《光纤陀螺仪指标（国军标）》的定义，零偏不稳定性主要表征了光纤陀螺输出量围绕其均值变化的离散程度。其功率谱密度与频率成反比，零偏不稳定性噪声的角速率功率谱为：
$$S_{\Omega }(f)=B^2/(2\pi f)$$
上式中$B$为零偏不稳定性系数，对应的方差计算公式如下：
$${\sigma }_{BI}^2(\tau )=4{\int }_0^{\infty }\frac{B^2}{2\pi f}\frac{{\sin }^4(\pi f\tau )}{(\pi f\tau {)}^2}\mathrm{d}f=\frac{2B^2}{\pi }{\int }_0^{\infty }\frac{{\sin }^4(\pi f\tau )}{(\pi f\tau {)}^3}\mathrm{d}(\pi f\tau )\approx \frac{4B^2}{9}$$
所以，在$\tau -{\sigma }_{BI}(\tau )$双对数图上，零偏不稳定性的斜率为0，它（或延长线）与 $\tau =1$的交点纵坐标读数为$2B/3$，如下图所示。

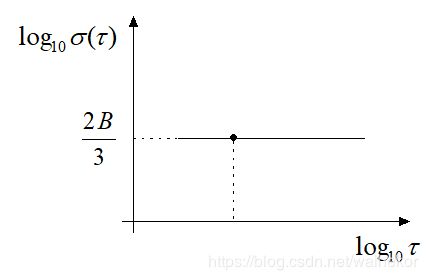
零偏不稳定性噪声具有低频特性，在陀螺输出中表现为零偏随时间的缓慢波动。

4．角速率随机游走（Rate Random Walk，RRW）

和角速度随机游走的概念类似，如果陀螺角加速率建模为高斯白噪声，则角速率表现为随机游走现象。
角加速率的功率谱为：

$$S_{{\Omega }^{\prime }}(f)=K^{\prime }$$
根据功率谱相关性质，得到角速率的功率谱公式如下：
$$S_{{\Omega }^{\prime }}(f)=K^{\prime }$$
所以：
$${\sigma }_{RRW}^2(\tau )=4{\int }_0^{\infty }\frac{K^2}{(2\pi f{)}^2}\cdot \frac{{\sin }^4(\pi f\tau )}{(\pi f\tau {)}^2}\mathrm{d}f=\frac{K^2\tau }{\pi }{\int }_0^{\infty }\frac{{\sin }^4(\pi f\tau )}{(\pi f\tau {)}^4}\mathrm{d}(\pi f\tau )=\frac{K^2\tau }{3}$$
因此，在$\tau -{\sigma }_{RRW}(\tau )$双对数图上，角速率随机游走的斜率为$1/2$，它（或延长线）与 $\tau =1$交点的纵坐标读数为$K/\sqrt{3}$，如下图所示。

5．速率斜坡（Rate Ramp，RR）

如果陀螺仪的角速率输出随时间缓慢变化，比如由于环境温度变化，角速率$\Omega$与测试时间$t$之间呈现线性关系，即：
$$\Omega (t)=\Omega (0)+Rt$$
上公式中$R$为速率斜坡系数，根据艾伦方差的定义公式：
$$y_i(\tau )=\frac{\left[\Omega (0)+R{t}_i\right]+\left[\Omega (0)+R\left(t_i+\tau \right)\right]}{2}=\Omega (0)+R{t}_i+\frac{R\tau }{2}$$
$$y_{i+1}(\tau )=\frac{\left[\Omega (0)+R\left(t_i+\tau \right)\right]+\left[\Omega (0)+R\left(t_i+2\tau \right)\right]}{2}=\Omega (0)+R{t}_i+\frac{3R\tau }{2}$$
所以有：$${\sigma }_{RR}^2(\tau )=\frac{1}{2}⟨{\left[y_{i+1}(\tau )-y_i(\tau )\right]}^2⟩=\frac{1}{2}⟨(R\tau {)}^2⟩=\frac{R^2{\tau }^2}{2}$$
可见，当角速率误差随时间线性变化时，将在$\tau -{\sigma }_{RR}(\tau )$双对数图上得到斜率为1的直线，它（或延长线）与$\tau =1$的交点纵坐标读数为$\mathrm{R}/\sqrt{2}$，如下图所示。

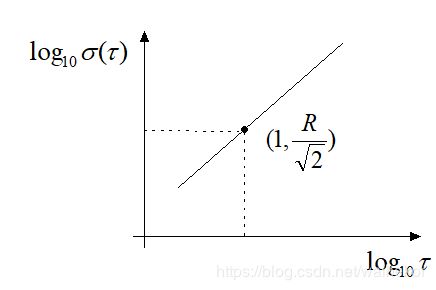
实际上，角速率斜坡更像是一种确定性的误差，而不是随机误差。角速率斜坡常常由系统误差引起的，比如环境温度的缓慢变化，通过严格的环境温度控制或者引入补偿机制可以降低此类误差。

5种艾伦方差汇总介绍与单位转换

上面介绍了5种噪声参数和Allan方差之间的关系，实际系统输出信号的功率谱不一定是单一斜率的，而可能由几种统计独立的线性功率谱叠加组合而成，若将该总功率谱作为Allan方差滤波器的输入，则陀螺误差的Allan方差分析结果可写为：
$${\sigma }_A^2(\tau )={\sigma }_{QN}^2(\tau )+{\sigma }_{ARW}^2(\tau )+{\sigma }_{BI}^2(\tau )+{\sigma }_{RRW}^2(\tau )+{\sigma }_{RR}^2(\tau )$$
整理可得到：
$${\sigma }_A^2(\tau )={\sigma }_{QN}^2(\tau )+{\sigma }_{ARW}^2(\tau )+{\sigma }_{BI}^2(\tau )+{\sigma }_{RRW}^2(\tau )+{\sigma }_{RR}^2(\tau )$$
需要注意的是上公式是在国际单位制上推导出来的，上式中的 ${\sigma }_A(\tau )$和$\tau$的单位分为是 $rad/s$和$s$，由此可得到各种噪声系数的单位，即：

$$Q-\mathrm{r}\mathrm{a}\mathrm{d},N-\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{s}}^{1/2},B-\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s},K-\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{s}}^{3/2},R-\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{s}}^2$$
但是我们习惯上${\sigma }_A(\tau )$常以$\left({}^{\circ }\right)/\mathrm{h}$为单位，并且并且各项误差系数也常使用$°$和$h$的组合作为单位，为了达到该目的，根据换算关系$\mathrm{lrad}/\mathrm{s}=\frac{180/\pi }{1/3600}\left({}^{\circ }\right)/\mathrm{h}$} ，进行如下转换：
$$\begin{array}{l}{\sigma }_A^2(\tau ){\left(\frac{180/\pi }{1/3600}\right)}^2=\frac{3(Q\times 180/\pi \times 3600{)}^2}{{\tau }^2}+\frac{{\left[N\frac{180/\pi }{(1/3600{)}^{1/2}}\times 60\right]}^2}{\tau }\\ +\frac{4{\left(B\frac{180/\pi }{1/3600}\right)}^2}{9}+\frac{{\left[K\frac{180/\pi }{(1/3600{)}^{3/2}}\times \frac{1}{60}\right]}^2\tau }{3}+\frac{{\left[R\frac{180/\pi }{(1/3600{)}^2}\times \frac{1}{3600}\right]}^2{\tau }^2}{2}\end{array}$$

通过相应的变量替换：

$$\begin{array}{rl}& {\sigma }_A^{\prime }(\tau )={\sigma }_A(\tau )\frac{180/\pi }{1/3600}\left(\left({}^{\circ }\right)/\mathrm{h}\right),Q^{\prime }=Q\times 180/\pi \times 3600(")\\ & N^{\prime }=N\frac{180/\pi }{(1/3600{)}^{1/2}}\left(\left({}^{\circ }\right)/{\mathrm{h}}^{1/2}\right),B^{\prime }=B\frac{180/\pi }{1/3600}\\ & K^{\prime }=K\frac{180/\pi }{(1/3600{)}^{3/2}}\left(\left({}^{\circ }\right)/{\mathrm{h}}^{3/2}\right)R^{\prime }=R\frac{180/\pi }{(1/3600{)}^2}\left(\left({}^{\circ }\right)/{\mathrm{h}}^2\right)\end{array}$$

整理可得：
$${\sigma }_A^{\prime 2}(\tau )=\frac{3Q^{\prime 2}}{{\tau }^2}+\frac{{\left(60N^{\prime }\right)}^2}{\tau }+\frac{4B^{\prime 2}}{9}+\frac{{\left(K^{\prime }/60\right)}^2\tau }{3}+\frac{{\left(R^{\prime }/3600\right)}^2{\tau }^2}{2}=\sum _{k=-2}^2{A}_k^{\prime }{\tau }^k$$
上式非常重要，有了它，当我们画出Allan方差曲线后，就可以直接通过读图的方式，辨识出各种噪声参数。

艾伦方差辨识参数的误差问题

理论上，Allan方差是随机过程一个现实的一种时间平均，但是由于实际应用时总是基于有限长度样本数据计算的，因而与经典方差估计一样，Allan方差也可看作是一种估计或统计量，服从一定的概率分布。研究表明，Allan方差估计${\hat{\sigma }}_A(\tau )$的$1\sigma$均方根误差可近似为（以相对百分比表示）
$$E_A(\tau )=\frac{\left|{\hat{\sigma }}_A(\tau )-{\sigma }_A(\tau )\right|}{{\sigma }_A(\tau )}\approx \frac{1}{\sqrt{2(N/M-1)}}\times 100\%$$
上式中 $M$为样本长度，$N$为分组数据长度，$N/M$为分组数，上式表明表明分组数越少Allan方差的估计误差越大。

艾伦方差曲线的绘制方法

假设我们获得了一组平均角速率样本序列：
$${\bar{\Omega }}_1\left({\tau }_0\right),{\bar{\Omega }}_2\left({\tau }_0\right),{\bar{\Omega }}_3\left({\tau }_0\right),\cdots ,{\bar{\Omega }}_N\left({\tau }_0\right)$$
公式中${\tau }_0$为采样间隔，一般IMU的采样频率一般在几百$Hz$甚至上千$Hz$,一般在计算艾伦方差时会静止放置几个小时，但是由于样本序列的长度总是有限的，因此Allan方差计算只能给出理论值的一个估计。
下面给出实现Allan方差计算的具体步骤：

1. 首先计算取样时间为${\tau }_0$时的Allan方差：
   $${\hat{\sigma }}_A^2\left({\tau }_0\right)=\frac{1}{2(N-1)}\sum _{k=1}^{N-1}{\left[{\bar{\Omega }}_{k+1}\left({\tau }_0\right)-{\bar{\Omega }}_k\left({\tau }_0\right)\right]}^2$$
2. 其次将取样时间间隔加倍，记${\tau }_1=2^1{\tau }_0$和$N_1=[N/2]$，（$[\cdot ]$表示取整），在相继奇偶序号角速率之间作算术平均，即
   $${\bar{\Omega }}_k\left({\tau }_1\right)=\frac{{\bar{\Omega }}_{2k-1}\left({\tau }_0\right)+{\bar{\Omega }}_{2k}\left({\tau }_0\right)}{2}k=1,2,3,\cdots ,N_1$$
   组成新的取样时间间隔为${\tau }_1$的平均角速率序列，即：
   $${\bar{\Omega }}_1\left({\tau }_1\right),{\bar{\Omega }}_2\left({\tau }_1\right),{\bar{\Omega }}_3\left({\tau }_1\right),\cdots ,{\bar{\Omega }}_{N_1}\left({\tau }_1\right)$$
   显然新序列的长度减半（但可能相差1个数据，下同），计算取样时间为${\tau }_1$时的Allan方差，即：
   $${\hat{\sigma }}_A^2\left({\tau }_1\right)=\frac{1}{2\left(N_1-1\right)}\sum _{k=1}^{N_1-1}{\left[{\bar{\Omega }}_{k+1}\left({\tau }_1\right)-{\bar{\Omega }}_k\left({\tau }_1\right)\right]}^2$$
3. 再次将取样时间间隔加倍，记${\tau }_2=2{\tau }_1=2^2{\tau }_0$和$N_2=\left[N_1/2\right]$ ,计算平均角速率，即：
   $${\bar{\Omega }}_k\left({\tau }_2\right)=\frac{{\bar{\Omega }}_{2k-1}\left({\tau }_1\right)+{\bar{\Omega }}_{2k}\left({\tau }_1\right)}{2}k=1,2,3,\cdots ,N_2$$
   组成新的取样时间间隔为${\tau }_2$的平均角速率序列，即：
   $${\bar{\Omega }}_1\left({\tau }_2\right),{\bar{\Omega }}_2\left({\tau }_2\right),{\bar{\Omega }}_3\left({\tau }_2\right),\cdots ,{\bar{\Omega }}_{N_2}\left({\tau }_2\right)$$
   新序列的长度再次减半，计算取样时间为KaTeX parse error: Can't use function '$' in math mode at position 9: \tau_{2}$̲，时的Allan方差，即： \hat{\sigma}{A}^{2}\left(\tau{2}\right)=\frac{1}{2\left(N_{2}-1\right)} \sum_{k=1}^{{N_{2}-1}\left[\bar{\Omega}_{k+1}\left(\tau_{2}\right)-\bar{\Omega}_{k}\left(\tau_{2}\right)\right]}{2}$$
4. 如此反复将取样时间间隔不断加倍，记${\tau }_L=2{\tau }_{L-1}=2^L{\tau }_0$和$N_L=\left[N_{L-1}/2\right]$,直至最终序列的长度不小于2，得平均角速率序列为:
   $${\bar{\Omega }}_1\left({\tau }_L\right),\cdots ,{\bar{\Omega }}_{N_L}\left({\tau }_L\right)$$
   并计算取样时间为${\tau }_L$时的Allan方差，即:
   $${\hat{\sigma }}_A^2\left({\tau }_L\right)=\frac{1}{2\left(N_L-1\right)}\sum _{k=1}^{N_L-1}{\left[{\bar{\Omega }}_{k-1}\left({\tau }_L\right)-{\bar{\Omega }}_k\left({\tau }_L\right)\right]}^2$$
   至此获得一系列的点对，${\tau }_i\sim {\hat{\sigma }}_A^2\left({\tau }_i\right)$或${\tau }_i\sim {\hat{\sigma }}_A\left({\tau }_i\right)$，$(i=1,2,3,\cdots ,L)$，完成Allan方差估计，并将结果绘制成双对数图。
   从上述计算过程可以看出，在${\tau }_0$基础上取样间隔时间是以2的倍数递增的，即取样时间为2的幂次方倍，而在一般应用中不需计算其他时间间隔上的Allan方差值。还容易看出，Allan方差的计算过程比较简单，并且计算量也不大。

艾伦方差相关代码

下面给出艾伦方差曲线绘制的matlab代码，可以对应上面的步骤。

function [sigma, tau, Err] = avar(y0, tau0)
% 计算Allan方差
% 输入：y -- 数据(一行或列向量), tau0 -- 采样周期
% 输出：sigma -- Allan方差(量纲单位与输入y保持一致), tau -- 取样时间, Err -- 百分比估计误差
% 作者: Yan Gong-min, 2012-08-22
% example: 
%     y = randn(100000,1) + 0.00001*[1:100000]';
%     [sigma, tau, Err] = avar(y, 0.1);
    N = length(y0);
    y = y0; NL = N;
    for k = 1:inf
        sigma(k,1) = sqrt(1/(2*(NL-1))*sum([y(2:NL)-y(1:NL-1)].^2));
        tau(k,1) = 2^(k-1)*tau0;
        Err(k,1) = 1/sqrt(2*(NL-1));
        NL = floor(NL/2);
        if NL<3
            break;
        end
        y = 1/2*(y(1:2:2*NL) + y(2:2:2*NL));  % 分组长度加倍(数据长度减半)
    end
    subplot(211), plot(tau0*[1:N], y0); grid
    xlabel('\itt \rm/ s'); ylabel('\ity');
    subplot(212), 
    loglog(tau, sigma, '-+', tau, [sigma.*(1+Err),sigma.*(1-Err)], 'r--'); grid
    xlabel('\itt \rm/ s'); ylabel('\it\sigma_A\rm( \tau )');

从艾伦方差曲线中辨识噪声参数可以通过手动读图的方式，当然也可以通过自动化的形式，自动辨识出参数，下面代码是一个自动辨识角度随机游走参数的代码，主要步骤是：通过辨识的噪声参数对应到log曲线频率，通过查找最为接近的频率对应的纵坐标数据。
需要注意的是下面代码输入的陀螺仪单位是国际单位，为$rad/s$，如果使用$\mathrm{deg}/h$，需要注意单位的转换。

%% Noise Parameter Identification
% Find the index where the slope of the log-scaled Allan deviation is equal to the slope specified.

% Angle Random Walk
% The above equation is a line with a slope of -1/2 when plotted on a log-log plot of σ(τ)versusτ. 
% The value of N can be read directly off of this line at τ=1.
slope = -0.5;
logtau = log10(tau);
logadev = log10(adev);
dlogadev = diff(logadev) ./ diff(logtau);
[~, i] = min(abs(dlogadev - slope)); %找到slope=-0.5 最接近的点；

% Find the y-intercept of the line.
b = logadev(i) - slope*logtau(i); 
% Determine the angle random walk coefficient from the line.
logN = slope*log(1) + b;
% disp('random walks');
N =[10^logN]; %角度随机游走值，单位为：(rad/s/root-Hz)

% Plot the results.
tauN = 1;
lineN = N ./ sqrt(tau);
figure
loglog(tau, adev, tau, lineN, '--', tauN, N, 'o')
title('Allan Deviation with Angle Random Walk')
xlabel('\tau')
ylabel('\sigma(\tau)')
legend('\sigma', '\sigma_N')
text(tauN, N, 'N')
grid on
axis equal

艾伦方差应用实例

1.ADIS16465

下图是是ADI的一款6轴MEMS IMU的数据手册，型号是ADIS16465，手册中给出的噪声参数如下，注意其单位：

1. In-Run Bias Stability: $2.5^{\circ }/h$
2. Angular Random Walk: $0.15^{\circ }/\sqrt{h}$
   另外还可以看到其零偏重复性是$0.4^{\circ }/\mathrm{s}\mathrm{e}\mathrm{c}$，，还是挺大的，所以一般需要在开始上电后静置数秒得到零偏重复性。根据国军标的定义，零偏重复性为：在同样条件下及规定间隔时间内，多次通电过程中，陀螺仪零偏相对其均值的离散程度，以多次测试所得零偏的标准偏差表示。
   
   下图是ADIS16465静置2.5小时$Z$轴的数据，采样率为$200Hz$，从图中可以看出：曲线大致可以分成三段，最左边的斜率为 $-1/2$，即角度随机游走噪声，因为这里的纵坐标单位是$°/h$，横坐标$\tau =1$对应的纵坐标为 $7.2^{\circ }/h$，根据前面介绍的如下公式：
   $${\sigma }_A^{\prime 2}(\tau )=\frac{3Q^{\prime 2}}{{\tau }^2}+\frac{{\left(60N^{\prime }\right)}^2}{\tau }+\frac{4B^{\prime 2}}{9}+\frac{{\left(K^{\prime }/60\right)}^2\tau }{3}+\frac{{\left(R^{\prime }/3600\right)}^2{\tau }^2}{2}=\sum _{k=-2}^2{A}_k^{\prime }{\tau }^k$$
   从上式可知：
   $$N={\sigma }_{ARW}\cdot \frac{\sqrt{\tau }}{60}={\sigma }_{ARW}\sqrt{\frac{1}{3600}h}=\frac{\frac{7.2^{\circ }}{\sqrt{h}}}{60}=\frac{0.12^{\circ }}{\sqrt{h}}$$
   所以和数据手册中的Angular Random Walk相差不大。
   下面看零偏不稳定性，斜率为0对应的横坐标为 $41s$，纵坐标为$2.4°/h$ ，所以
   $$B=2.4^{\circ }/(2/3)/h=3.6^{\circ }/h$$
   可以看到和数据手册也相差不大，因为艾伦方差只能当成一种粗略的参数辨识手段，所以为了方便识图，这里当成$2.4°/h$ 更简单点。
   下面看角速率随机游走参数，这里看横坐标为$100s$时的数据，对应的纵坐标为$3.0°/h$，所以：
   $$K=\frac{60\sqrt{3}{\sigma }_{RRW}}{\sqrt{\tau }}=\frac{60\sqrt{3}\cdot 3.0}{\sqrt{100}}/h^{3/2}=31^{\circ }/h^{3/2}$$
   另外图中显示的数据平均值为$329°/h$，因为16465的零偏稳定性很小，只有$3.0°/h$，基本可以忽略不计，所以零偏重复性大概为$0.09^{\circ }/\mathrm{s}\mathrm{e}\mathrm{c}$，小于数据手册中的$0.4^{\circ }/\mathrm{s}\mathrm{e}\mathrm{c}$，但是仍然说明零偏重复性对系统影响巨大，在实际应用中需要很好的处理。
   
   下图是ADIS16465的加速度计参数
   
   下面是加速度三个轴的艾伦方差曲线，纵坐标单位为$g$，从图中可以看出，横坐标0.1到10之间的曲线的斜率大约为$-1/2$，所以该段曲线为速度随机游走误差， 横坐标$10^0$所对应的的纵坐标大约为$20ug$，即$0.012\frac{m}{s\sqrt{h}}$， 和数据手册给出的值相当。
   横坐标为10 的地方的斜率大约为0，所以该点对应的是零偏不稳定性噪声，读图可知，零偏不稳定性噪声 X轴略大，为$34ug$，Y轴和Z轴轴的数据大致相同，为$20ug$，比数据手册中给出的略大。
   

1.ADIS16470

下图是ADIS16470静置2小时Z轴的采样的数据，采样率为$200Hz$，可以看到大致可以分成两段，角速率随机游走参数已经很小了。

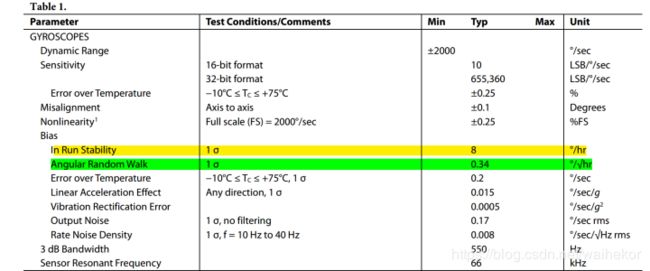
数据手册参数如下：

1. In-Run Bias Stability:$8^{\circ }/h$
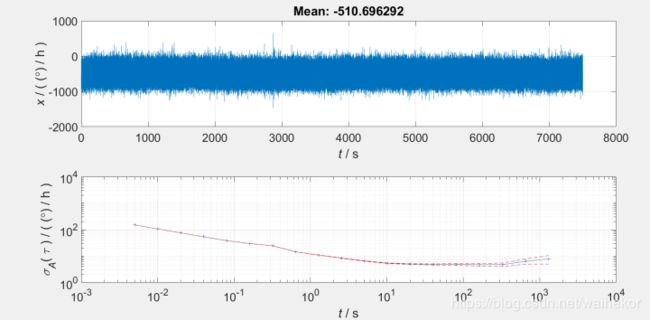
2. In-Run Bias Stability:$0.34^{\circ }/\sqrt{h}$
   
   $$\begin{array}{c}N={\sigma }_{ARW}\cdot \frac{\sqrt{\tau }}{60}={\sigma }_{ARW}\sqrt{\frac{1}{3600}h}=\frac{\frac{12^{\circ }}{\sqrt{h}}}{60}=\frac{0.2^{\circ }}{\sqrt{h}}\\ B=5^{\circ }/(2/3)/h=7.5^{\circ }/h\end{array}$$

下图是ADIS16470的加速度计噪声参数。

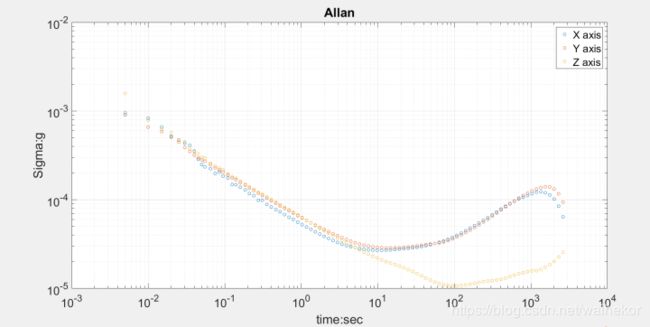
下图是ADIS16470的加速度艾伦方差曲线，可以看到横坐标10之前的曲线的斜率大概为 $-1/2$，即为速度随机游走部分曲线，当横坐标为1时，纵坐标为$60ug$，可得速度随机游走噪声为：$0.036\frac{m}{s\sqrt{h}}$，和数据手册中的 噪声相当。
当横坐标为10时，斜率为0，对应的是零偏不稳定性，可得零偏不稳定性噪声大约为$45ug$，比数据手册中的参数略大。

3.某型号光纤惯导

下图是光纤陀螺静置1.5个小时的采样数据，采样率为$100Hz$，可以看出曲线的后半段为角度随机游走噪声，零偏不稳定性在图中没有显示出来，可能采样时间还是短了些。

$$N={\sigma }_{ARW}\cdot \frac{\sqrt{\tau }}{60}=0.14\cdot \frac{\sqrt{100^{\circ }}}{60\sqrt{h}}=\frac{0.0023^{\circ }}{\sqrt{h}}$$

另外从光纤陀螺的的数据均值可以看出，相比Mems陀螺仪的零偏重复性已经非常小了，图中的均值并不能反映零偏，因为没有去除地球自转角速度在Z轴的分量。

10s平滑计算零偏不稳定性

国军标中常用10s平滑方法计算零偏不稳定性，这里比较下它和艾伦方差在计算零偏稳定性之间的数值差异。10s平滑主要思路是每10s计算下均值，再计算这些均值的方差，例如有1000s的数据，需要计算100个均值，并求这100个均值的方差。主要参考代码如下：

for i=1:3
    %Bias stability and Bias
    Smo=10;%N 10秒平滑
    num=Smo/t0;%%m每组内数据个数
    m=floor(length(Wb(:,i))/num);%%共可以分成m组数据
    gx=zeros(m,1);
    Xbais_all = mean(Wb(:,i));
    for j=1:m-1
        gx(j)=mean(Wb(1+(j-1)*num:1+j*num,i)); %取平均
    end
    gx= gx(2:end-2,:);
    Xbais_stability = std(gx); % 计算标准差
    fprintf('Bias Stability 10s:%0.2e [deg/h]\n',Xbais_stability);
end

1. 光纤陀螺的10s平滑结果为：$4.62^{\circ }/h$
2. ADIS16470的10s平滑结果为：$13.3^{\circ }/h$；艾伦方差：$7.5^{\circ }/h$
3. ADIS16465的10s平滑结果为：$29.1^{\circ }/h$；艾伦方差：$3.6^{\circ }/h$

可看到10平滑方法计算出来的零偏稳定性相对艾伦方差较大，不知道有没有理论证明。
下面是加速度计的10s平滑结果：

1. ADIS16465：$X$轴$99ug$，$Y$轴$26ug$，$Z$轴$29ug$;
2. ADIS16470：$X$轴$4.24mg$，$Y$轴$6.17mg$，$Z$轴$0.46mg$;
3. 光纤惯导：$X$轴$97ug$，$Y$轴$53ug$，$Z$轴$150ug$;

参考文献

1. 惯性仪器测试与数据分析 严恭敏
2. Analysis and Modeling of Inertial Sensors Using Allan Variance