小全读论文《Learning without Memorizing》CVPR2019
小全读论文《Learning without Memorizing》CVPR2019
- 一、Motivation
- 二、Approach
- 注意力区域的特征生成(Generating attention maps)
- 注意力区域的知识蒸馏
- 三、实验结果
一、Motivation
本文关注的是增量学习问题,增量学习问题一般的解决方案是利用一个额外的磁盘间存储***少量***旧类别的样本。文章认为这一设置会存在以下问题:
1)不适合大规模的量化学习问题,如life-long learning设置,当类别很多的时候,依然需要耗费很多的存储空间;
2)在工业场景中,我们往往只会把最终的模型给终端使用者,而不会把数据给到他们(出于隐私等问题),因此,终端使用者是无法接触到旧类别的数据的;
3)与人类的机制违背。人在学习新类别过程往往不会反复地观测旧类别的数据,但依然能达到比较好的学习效果
因此本文提出了一个 不需要接触旧类别样本 的增量学习方法,解决这个问题的一个核心思想是如何保留旧模型的知识,传统的方法是采取知识蒸馏的约束项,这个约束项的意义是 对于一张图片 I n I_n In,新模型尽可能去学习或者保留这张图片在旧模型中可能会被预测的旧类别 。
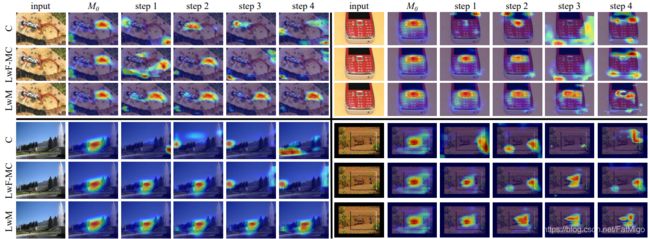
然而,作者认为,图片中某些区域的点(称为注意力区域)会对预测的特定类别的结果有比较重要的影响,即预测成A类别的置信度是0.1,其主要是由某些区域得到的,而对于B类别,可能又是另外一个区域得到的。但是上述的知识蒸馏的约束项却忽略了对预测结果有重要影响的区域,即对于一个样本,这个约束项只限制预测结果必须要是A类别置信度是0.1,但是并不约束A类别的注意力区域和旧模型的一致,导致存在一些情况,即使预测结果一致,但是注意力区域是完全不同的,如下图所示

注意力区域的一个重要意义是,可认为是 当前预测类别结果(置信度)的一种解释,这是旧模型的一个很重要的知识(knowledge),因此本文提出了一个Attention Distillation Loss (LAD),通过限制样本的注意力区域,让新模型可以保留旧模型中的知识。
二、Approach
本文需要解决两个很关键的问题,
1)如何定义或者生成注意力区域
2)如何对注意力区域进行约束和限制,也即对注意力区域的知识蒸馏
注意力区域的特征生成(Generating attention maps)
本文采取Grad-CAM来生成注意力区域,具体地,
1)首先图片会输入到模型中进行前向传播,得到每一个类别的置信度 y c y_c yc。
2)然后对 y c y_c yc进行反向传播,可以计算到每个卷积层每层feature map上的梯度值 A k A_k Ak
3)最后对 A k A_k Ak做一个GAP(global average pooling)操作,得到一个置信值 α k \alpha_k αk,这个置信值作为这层feature map的重要程度
4)然后,记 α = [ α 1 , α 2 , . . . , α K ] , A = [ A 1 , A 2 , . . . , A K ] \alpha=[\alpha_1,\alpha_2,...,\alpha_K], A=[A_1,A_2,...,A_K] α=[α1,α2,...,αK],A=[A1,A2,...,AK], 文章把注意力区域的特征定义为
按照 Grad-CAM原论文的理解,最后一步本质就是 按 α k \alpha_k αk对 A k A_k Ak进行加权求和,然后接一个relu消除负元素
!!!讨论:在这个章节上我有几点想展开讨论
1.数学符号好像有bug,首先在数学符号中, α = [ α 1 , α 2 , . . . , α K ] , A = [ A 1 , A 2 , . . . , A K ] \alpha=[\alpha_1,\alpha_2,...,\alpha_K], A=[A_1,A_2,...,A_K] α=[α1,α2,...,αK],A=[A1,A2,...,AK],逗号表示按列添加元素,所以 α \alpha α的维度是 1 ∗ K 1*K 1∗K, A A A的维度是 M ∗ K M*K M∗K, M M M表示feature map的大小。因此 α T , A \alpha^T,A αT,A是无法做矩阵乘的,如果是按照Grad-CAM的做法的话,正确的表示方式应该是Q = R e L U ( A α T ) Q=ReLU(A\alpha^T) Q=ReLU(AαT)
2.为什么梯度值可以认为是重要性程度的表现?
本人有两种理解, -
–首先,以网络最后一层全连接层的运算为例,最后一层的运算可以看成 σ ( W c X + b ) \sigma(W_cX+b) σ(WcX+b), W c W_c Wc表示第c类的分类器参数,所以 X j X_j Xj的梯度其实对应的是 W c j W_{cj} Wcj,梯度越大,表示 X j X_j Xj在前向运算的系数 W c j W_{cj} Wcj越大,因此表示 X j X_j Xj越大。其他的卷积层也可以类似的理解
–其次,根据梯度的定义,梯度表示的是函数在一个点上的变化率,即梯度越大,表示这个点的一小点变化,会给最终的函数值带来很大的改变。因此梯度值可以认为是重要性程度的表示。额外提一点,若梯度值是正的,表示这个点的值变大,其函数值便会变大,反之则变小
3.为什么需要过ReLU?
如上述第二个问题的第二点解释,梯度值是正的的时候,随着 X j X_j Xj的变大,最终的 y c y_c yc才会增大,因此我们只关注那些对函数有正向影响的点。
注意力区域的知识蒸馏
本文提出了一个Attention distillation loss L A D L_{AD} LAD实现对注意力区域的知识蒸馏。记 t t t为不同的增量步骤,具体的对于输入图片 i i i,首先提取 t − 1 t-1 t−1和 t t t时刻的注意力区域
Q t − 1 i , c = v e c t o r ( G r a d C A M ( i , M t − 1 , c ) ) Q t i , c = v e c t o r ( G r a d C A M ( i , M t , c ) ) \begin{aligned} Q_{t-1}^{i,c}=vector(GradCAM(i, M_{t-1},c))\\ Q_{t}^{i,c}=vector(GradCAM(i, M_{t},c)) \end{aligned} Qt−1i,c=vector(GradCAM(i,Mt−1,c))Qti,c=vector(GradCAM(i,Mt,c))
然后计算
L A D = ∑ j = 1 l ∣ ∣ Q t − 1 , j I n , b ∣ ∣ Q t − 1 I n , b ∣ ∣ 2 − Q t , j I n , b ∣ ∣ Q t I n , b ∣ ∣ 2 ∣ ∣ \begin{aligned} L_{AD}=\sum_{j=1}^l||\frac{Q_{t-1,j}^{I_n,b}}{||Q_{t-1}^{I_n,b}||_2} - \frac{Q_{t,j}^{I_n,b}}{||Q_{t}^{I_n,b}||_2} || \end{aligned} LAD=j=1∑l∣∣∣∣Qt−1In,b∣∣2Qt−1,jIn,b−∣∣QtIn,b∣∣2Qt,jIn,b∣∣
其中 l l l表示把注意力区域拉成一个向量后的长度, b b b表示在旧类别中置信度最高的类别, I n I_n In表示第 n n n张图片。
注意:
- 文章并不是采取全部的旧类别进行知识蒸馏,而是只采取旧类别中置信度最高的那个类别,
- 其次在进行知识蒸馏前,会对注意力区域的特征进行L2归一化操作。
- 文章采取L1差异性对新旧注意力区域进行约束,作者说明到实验结果L2比L1的效果要好。作者同时也指出,本质上这是在寻求新旧模型在样本梯度上的近似性,从而从梯度角度保留旧模型的信息。
最终的损失函数形式如下
L l w m = L C + β L D + γ L A D \begin{aligned} L_{lwm}=L_C+\beta L_D+\gamma L_{AD} \end{aligned} Llwm=LC+βLD+γLAD
总共由三个loss组成,分别是分类的loss,传统的知识蒸馏的loss以及本文提出的基于注意力区域的loss。