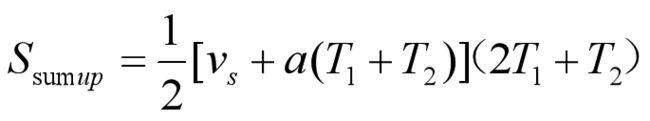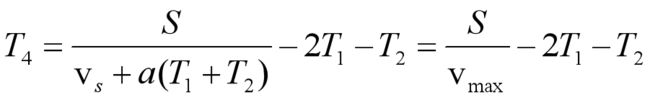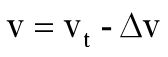步进电机驱动算法——S形加减速算法原理

步进电机S形加减速简介

一个物体从起点运动到终点要经历加速、匀速、减速的过程，把整个过程中速度随时间变化关系画出来，就是速度曲线。
“S”形加减速就是指速度曲线中加减速阶段的曲线呈现一个英文字母“S”型。
“S”形加减速的曲线并没有限定是什么曲线，所以可以是指数曲线，可以是正弦曲线，这里分析的“S”形加减速是基于加速度匀速变化的曲线。
基于加速度匀速变化的S形加减速可分为：
7段：加加速段（T1）、匀加速段（T2）、减加速段（T3）、匀速段（T4）、加减速段（T5）、匀减速段（T6）、减减速度段（T7）。
6段：加加速段（T1）、匀加速段（T2）、减加速段（T3）、加减速段（T5）、匀减速段（T6）、减减速度段（T7）。
5段：加加速段（T1）、减加速段（T3）、匀速段（T4）、加减速段（T5）、减减速度段（T7）。
4段：加加速段（T1）、减加速段（T3）、加减速段（T5）、减减速度段（T7）。

七段S形加减速算法原理分析

加速/减速开始时速度比较缓慢，然后逐渐加快，在加速/减速接近结束时速度再次缓慢下来，从而使移动较为稳定。

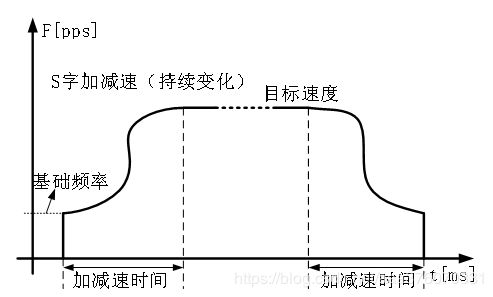
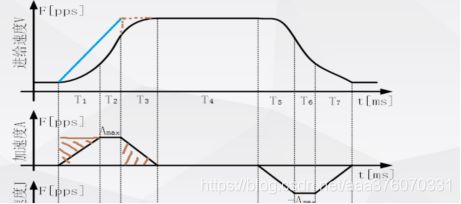
“S”形曲线加减速将传统的3段加减速过程变为7段加减速过程，形成S字形。“S”形曲线由加速段（T1）、匀加速段（T2）、减加速段（T3）、匀速段（T4）、减速段由加减速段（T5）、匀减速段（T6）、减减速度段（T7）组成。

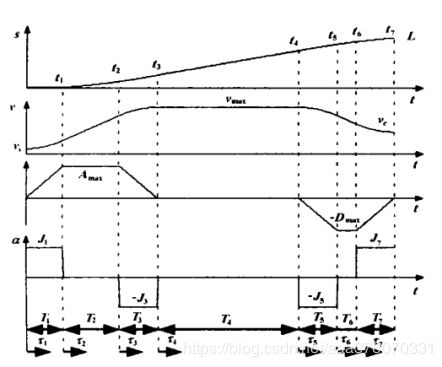
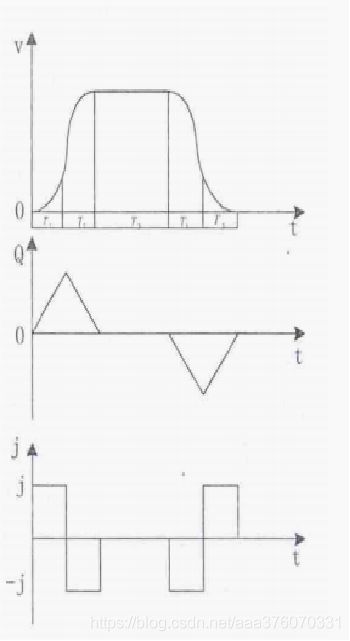
位移，速度，加速度，加加速度如图所示。
设初速度为Vs，末速度为Ve，最大速度为Vmax。加加速度J记为Jmax。根据S曲线对称性，当可以达到最大速度时，其中T1=T3，T5=T7。
tk(k=0,1,…7) ：表示各个阶段的过渡点时刻，虚线对应的时刻；
Tk(k=1,…7)：各个阶段的持续运行时间。
τk(k=0,1,…7)：局部时间坐标，表示以各个阶段的起始点作为时间零点的时间表示，τk表示以第K段某一时刻与该段起点时刻的时间差。这样以τk作为每一段的自变量，以上一段结束时的速度作为本段的初速度，每一小段单独计算速度值可以大大简化速度表达式，分段计算的思想可以为计算和程序设计带来很大方便。相当于每个段都把竖轴移到虚线处。

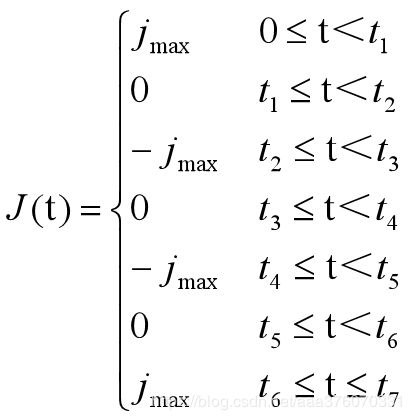
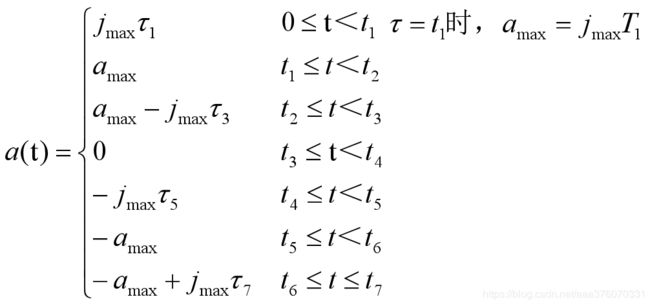
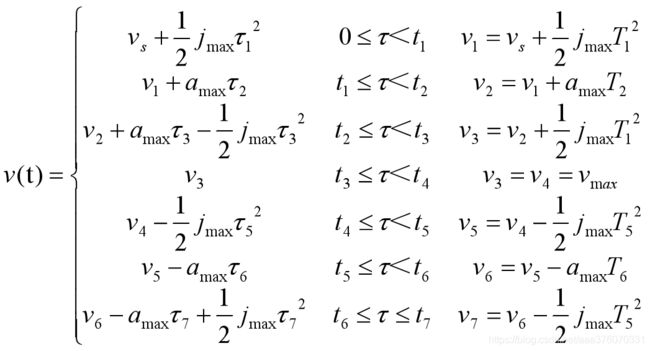
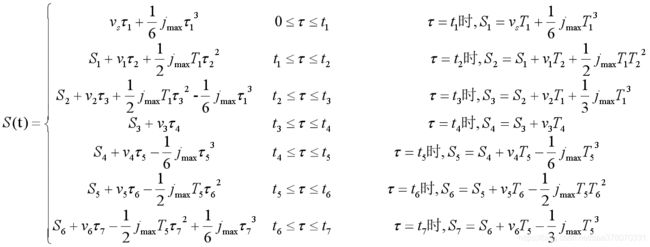
传统的七段S曲线是一个完整段数学模型，但在实际应用中S曲线是否存在匀速段取决于速度达到给定速度时，加速段和减速段位移之和是否小于实际需要运行段位移。加速及减速过程中是否存在匀加速段或匀减速段则由步进电机段初始速度Vs、最终速度Ve、加速度amax和加加速度J共同决定。
由S曲线特性可知，加加速段和减加速段对称。且在加速过程中，应尽量满足使加速度a可达到amax。所以，匀加速段存在段条件是给定速度V和初速度Vs之差不小于 ：
1）若 ，则加速过程中存在匀加速段，最大加速度能够达到amax，加速过程中的加加速段时间、匀加速段时间、减加速段时间为：

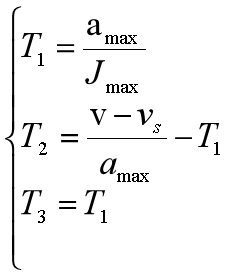
2）若 ，则加速过程中不存在匀加速段，最大加速度不能够达到amax，加速过程中的加加速段时间、匀加速段时间、减加速段时间为：

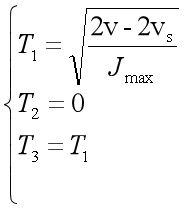
由于S曲线的减速段跟加速段对称，按照同样的思路可得出减速阶段加减速时间，匀减速时间和减减速时间为：
1）在 的情况下

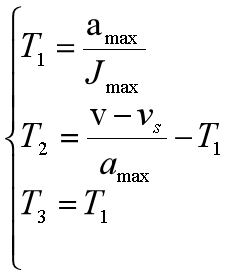
2）在 ，的情况下：

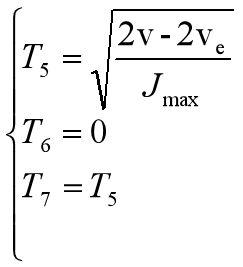
还剩下匀速段时间未求：
用SAcc表示步进电机在加速阶段的位移、SDec表示减速段的位移，S表示实际需要运行的位移，则：
1）当 时，S曲线中存在匀速运行的阶段，此时
2）当 时，S曲线中不存在匀速运行的阶段，此时 。
至此，全部参数以及确定，在应用时可以根据实际情况规划需要的S曲线。
几个中间计算式推导：

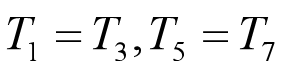
加加速度为J保持不变，加速度最大值为amax，那么时间T1为：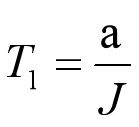
加速度曲线为梯形，梯形面积为速度最大值Vmax，初试速度为Vs，可得
匀加速段时间T2：

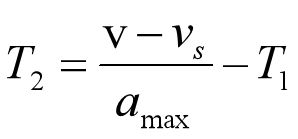
割补一下面积，相当于变成了T型加减速。
T4的另一种推法：
匀速段时间T4的大小与位移S有关，如果加速段曲线和减速段曲线对称。
设加速段（1,2,3段对应的加加速，匀加速，减加速）位移之和为
那么减速段位移之和也是 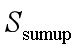， 可得：

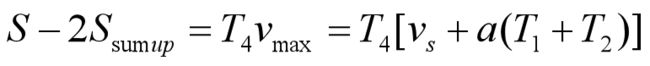
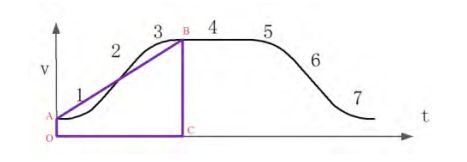
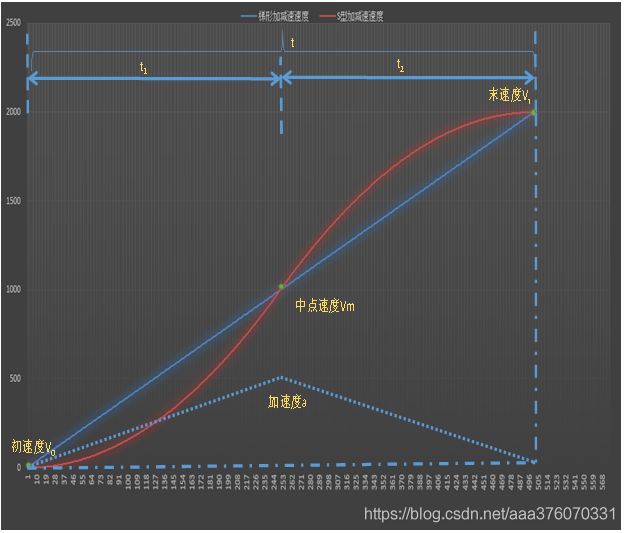
根据对称性，在下图中的线段AB与S曲线围城的两个区域面积相等，那么梯形OABC的面积就等于加速段的位移，所以：
梯形面积公式，1/2上底加下底再乘高，其中T1=T3

将上式带入上上式，可得匀速段持续时间T4：

五段S形加减速算法实现

假设给定条件：加速段的末速度，初速度，加速时间，以此来计算控制步进电机的每一步速度。
加速段由加加速段(IncAccel)和减加速段(DeAccel)组成。
因为T1=T2，T4=T5，为了简化算法初速度V0和最终速度Ve都为0，使T1=T2=T4=T5=T，那么T和T3确定了加加速度，加速度，速度，位移之间的关系就确定了。
加加速段是加速度关于时间的斜率为正的直线，减加速段则是加速度关于时间的斜率为负的直线。
加速度从0开始变化，到了一定值开始减小，最后为0，由于加速度的斜率是相同的，所以加加速度段和减加速度段，所用的时间是一样。这两段曲线是关于加速度最大值的对应的速度中心对称的。

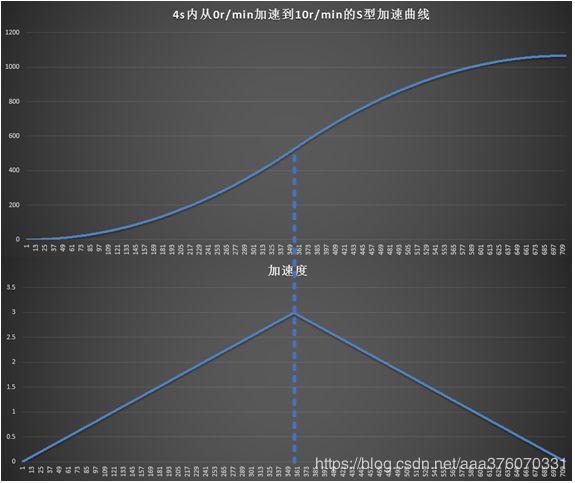
针对加加速段分析：

算法分析

准备工作（推导方法和前面一致）：
针对加加速段分析，此时 ，且初速度V0=0：
当加速度从0变化到最大值，有
J为加加速度（Jerk），对加速度积分面积就是速度，


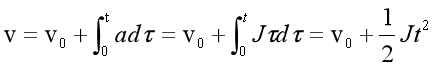
速度的变化量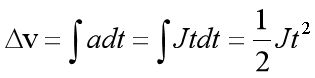： ，那么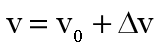

只要知道J即可得到加加速段的速度变化，当加速度变化到最大值时，此时
速度（V）=中点速度(VM)，可得：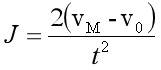
其中：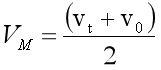

vt为末速度，是减加速段最终的速度值，而这一段的距离可以求得：

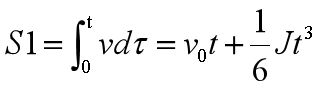
针对减加速段分析，此时 ，且此阶段初速度为上个阶段的末速度v，此阶段末速度为vt。
当加速度从最大值变化到0，有
J为加加速度（Jerk），对加速度积分面积就是速度，


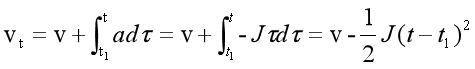
速度的变化量：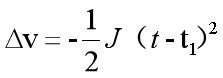

那么 ，整理成此步是为了方便建立速度表。

而这一段的距离可以求得（平均速度乘时间减去加加速段位移）：


整理一下可得：

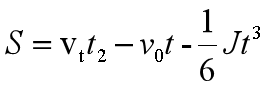
对速度而言，只要t变化足够小，即dt小，那么速度变化就越平滑，得到的速度点拟合出来的曲线就越接近目标曲线。
根据以上速度公式只要给定一个合适的时间t，比如在2s内加速了1000步，即
，那么t1为第一步的时间，t2为第一步和第二步的时间……（离散时间的方法）
步进电机速度单位为r/min时，可以把单位转换为step/s，方法为：假设速度为5r/min，5细分数（电机转动一圈脉冲数）/60。 其中60为60秒，将r/min转换成了step/s。
同时，步进电机是1个脉冲走1步并旋转一定角度，当电机速度单位为step/s时，速度就等于脉冲间隔频率，即speed=Freq。因为脉冲间隔频率单位为hz，Ahz即1秒产生A个脉冲，可以驱动电机走A步，速度单位为step/s，Astep/s也即1秒电机走A步。

查表法编程实现思路及方法

使用查表法如何实现：
对加速段建立速度表，速度单位为step/s时，速度表即为频率表。频率的倒数为时间，C*tt=时间，其中C为定时器计数值，tt为定时器计数周期。最终需要落实到定时器计数值。想让速度曲线为S曲线，在加加速段，频率（速度）的增量由小变大，C由大变小，在减加速段，频率（速度）的增量由大变小，C由小变大。
对减速段则将速度表逆序即可实现减速。
同样的在定时器中断里，设置状态标志：加速，减速，匀速，停止以实现功能。

1.根据已知的速度条件（初速度，末速度）和加速时间，可以求得加加速度J，根据位移公式：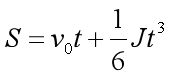

可以求得加加速需要的步数，那么减加速步数=平均速度乘时间-加加速步数也可求得。
2.初始化一个速度表用于存速度，注意速度的单位应当转化为step/s。

3.根据位移公式 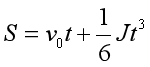，计算走一步的时间，即S=1，此时V0,J,S都已知，
可算出t，记为ti。这个ti就是前面前面提到的离散时间的思想，t1为第一步的时间，t2为第一步和第二步的时间，t2=2*t1……
使用一个简单的for循环来描述：
for（i=1;i<加加速步数;i++）
{
Sumt += Ti; //这样就能计算出1到n步的时间
}
for（i=1;i<加加速步数;i++）
{
Sumt += Ti;
DeltaV = 0.5f * Jerk * pow(Sumt,2);
Speed.VelocityTab[i] = Speed.Vo + DeltaV;
}
这样就计算出了速度的增量，并建立出了加加速阶段的速度表。
值得注意的是当最后一步的时候,时间并不严格等于加加速度时间，还需要处理。

可以在最后一步的前一步不采用累加时间的方式，而是
Sumt = fabs(Sumt - 加加速段时间 )这样来减小误差。
其中DeltaV = 0.5f * Jerk * pow(Sumt,2);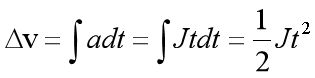
Speed.VelocityTab[i] = Speed.Vo + DeltaV;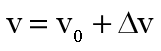
同理对于减加速阶段，建立速度表：

DeltaV = 0.5f * Jerk * pow(fabs( Time - Sumt),2)

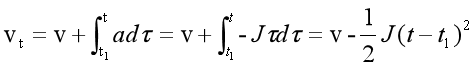
Speed.VelocityTab[i] = Speed.Vt - DeltaV;

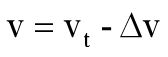
至此，整个加速段的速度表建立完毕，而减速段速度表只需要将表倒序。
速度表最终需要落实到定时器计数值上：因为速度表等于脉冲频率表，频率的倒数为时间δt，而C*tt=δt，其中C为定时器计数值，tt为定时器计数周期。
有了这个C值，即可产生PWM波。

4.如何产生PWM波及TIMx定时器配置
使用定时器来产生PWM波：定时器计数器，初始输出低电平，计数小于num值时，输出高电平，大于num值小于2*num值时，输出低电平。这样就产生了一个脉冲。
定时器配置模式可以选择输出比较模式，使用此模式输出PWM波，简单来说就是当计数器与捕获/比较寄存器当前值匹配时，输出比较功能做出不同的动作。比如：当计数器比捕获/比较寄存当前值小时，输出高电平，达到比较值（捕获/比较寄存器当前值）后，翻转电平输出低电平。再重新设置新的比较值，如此反复，即可输出PWM波。

S曲线加减速流程图

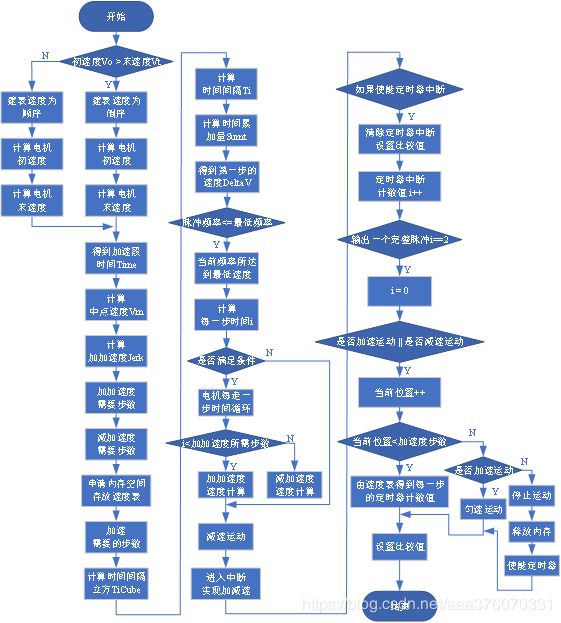
注意事项：
“S”形加减速算法设计通过初速度、末速度、中点速度等参数来进行对算法的编写。如果要进行加减速控制首先要建立速度表，建立表时需注意初速度比末速度大时做减速运动，数值变化跟加减运动相同，然后判断建表时速度是倒序还是顺序。建立表最重要的一点就是建表时需申请内存空间存放速度表（malloc），申请内存空间之后一定要记得释放空间（free）。
当建立速度表之后首先要计算第一步速度，根据第一步的速度值达到下一步的时间，步进电机的速度就是定时器脉冲输出频率，即可得到计算每一步的时间。
“S”形做加减速运动时，步进电机如果为运行状态，第一步的速度是0，则定时器从0xFFFF开始，定时器中断服务函数实现加减速运动。中断服务函数通过速度表得到每一步的定时器计数值，然后运动结束之后要释放内存。