概率编程库Pymc3案例之线性回归

参考：https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers

1、模型假设

贝叶斯线性回归模型，假设参数具有正态分布（Normal）先验，要预测的具有正态分布的观测值 Y ，其期望 μ 是两个预测变量的线性组合， X1 和 X2 ：

Y∼N(μ,σ2)

μ=α+β1X1+β2X2Y

其中 α 是截距， βi是变量 Xi的系数； σ 代表观察误差。

模型中的未知变量需要赋予先验分布，假设服从零均值的正态先验。其中，系数 α 、 βi的方差为100，选择半正态分布作为观测误差 σ的先验分布。

α∼N(0,100)

βi∼N(0,100)

σ∼|N(0,1)|

2、模拟数据生成

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

np.random.seed(123)

alpha=1
sigma=1
beta =[1, 2.5]

N=100

X1=np.random.randn(N)
X2=np.random.randn(N)

Y=alpha + beta[0]*X1 + beta[1]*X2 + np.random.randn(N)*sigma

%matplotlib inline
fig1,ax1 = plt.subplots(1, 2, figsize=(10,4));
ax1[0].scatter(X1, Y);ax1[0].set_xlabel('X1');ax1[0].set_ylabel('Y'); 
ax1[1].scatter(X2, Y);ax1[1].set_xlabel('X2');ax1[1].set_ylabel('Y');

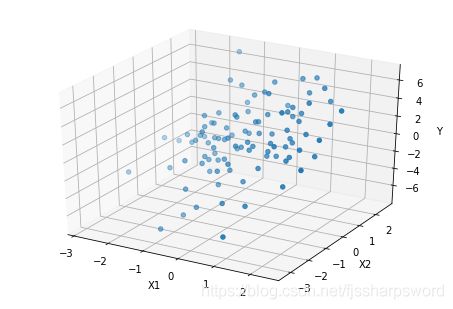
fig2 = plt.figure(2);
ax2 = Axes3D(fig2);
ax2.scatter(X1,X2,Y);
ax2.set_xlabel('X1');
ax2.set_ylabel('X2');
ax2.set_zlabel('Y');

2、利用pymc3定义模型

import pymc3 as pm 
with pm.Model() as basic_model:
    alpha=pm.Normal('alpha',mu=0,sd=10)
    beta=pm.Normal('beta',mu=0,sd=10,shape=2)
    sigma=pm.HalfNormal('sigma',sd=1)

    mu=alpha+beta[0]*X1+beta[1]*X2

    Y_obs=pm.Normal('Y_obs',mu=mu,sd=sigma,observed=Y)

定义了三个具有正态分布先验的随机性随机变量（stochastic random veriables）。

定义了一个确定性随机变量（deterministic random veriable）,确定性指这个变量的值完全由右端值确定。

最后定义了 Y 的观测值，这是一个特殊的观测随机变量（observed stochastic），表示模型数据的可能性。通过 observed 参数来告诉这个变量其值是已经被观测到了的（就是 Y 变量），不会被拟合算法改变。可以用 numpy.ndarry 或 pandas.DataFrame 对象作为数据参数传入。

3、模拟拟合

3.1 MAP方法

使用最优化方法找到点估计，快速简单。PyMC3提供了 find_MAP 函数，返回参数的一个估计值（point）。

默认情况下，find_MAP 使用Broyden–Fletcher–Goldfarb–Shanno (BFGS) 算法进行最优化运算，找到对数后验分布的最大值。这里也可以指定 scipy.optimize 模块中的其他最优化算法完成寻优。

map_estimate = pm.find_MAP(model=basic_model)
from scipy import optimize
map_estimate2 = pm.find_MAP(model=basic_model,fmin=optimize.fmin_powell)
print(map_estimate)
print(map_estimate2)

Optimization terminated successfully.
         Current function value: 148.980478
         Iterations: 6
         Function evaluations: 269
{'sigma': array(0.96298715), 'sigma_log__': array(-0.03771521), 'alpha': array(0.90661753), 'beta': array([0.94850377, 2.52246124])}
{'sigma': array(0.96298742), 'sigma_log__': array(-0.03771493), 'alpha': array(0.90661033), 'beta': array([0.94849417, 2.5224695 ])}

值得注意的是，MAP估计不总是有效的，特别是在极端模型情况下。在高维后验中，可能出现某一出概率密度异常大，但整体概率很小的情况，在层次化模型中较为常见。

大多数寻找MAP极大值算法都找到局部最优解，那么这种算法这在差异非常大的多模态后验中会失效。

3.2 MCMC方法

虽然极大后验估计是一个简单快速的估计未知参数的办法，但是没有对不确定性进行估计是其缺陷。相反，比如MCMC这类基于采样的方法可以获得后验分布接近真实的采样值。

为了使用MCMC采样以获得后验分布的样本，PyMC3需要指定和特定MCMC算法相关的步进方法（采样方法）,如Metropolis, Slice sampling, or the No-U-Turn Sampler (NUTS)。PyMC3中的 step_methods 子模块提供了如下采样器： NUTS, Metropolis, Slice, HamiltonianMC, and BinaryMetropolis。可以由PyMC3自动指定也可以手动指定。自动指定是根据模型中的变量类型决定的： 
* 二值变量：指定 BinaryMetropolis 
* 离散变量：指定 Metropolis 
* 连续变量：指定 NUTS

手动指定优先，可覆盖自动指定。

PyMC3有许多基本采样算法，如自适应切片采样、自适应Metropolis-Hastings采样，但最厉害是的No-U-Turn采样算法（NUTS），特别是在具有大量连续型参数的模型中。NUTS基于对数概率密度的梯度，利用了高概率密度的区域信息，以获得比传统采样算法更快的收敛速度。PyMC3使用Theano的自动微分运算来进行后验分布的梯度计算。通过自整定步骤来自适应的设置Hamiltonian Monte Carlo(HMC)算法的可调参数。NUTS不可用于不可微分变量（离散变量）的采样，但是对于具有不可微分变量的模型中的可微分变量是可以使用的。

NUTS需要一个缩放矩阵作为参数，这个矩阵提供了分布的大致形状，使NUTS不至于在某些方向上的步长过大而在另外一些方向上的步长过小。设置有效的缩放矩阵有助于获得高效率的采样，特别是对于那些有很多未知的（未被观察的）随机型随机变量的模型或者具有高度非正态后验的模型。不好的缩放矩阵将导致采样速度很慢甚至完全停止。此外，在多数时候，采样的初始位置对于高效的采样也是很关键的。

幸运的是，PyMC3使用自动变分推理ADVI (auto-diff variational inference)来初始化NUTS算法，并在 step 参数没有被指定的情况下会自动指定一个合适的迭代方法（step，采样器）。

with basic_model:
    #trace = pm.sample(2000)
    step = pm.NUTS()#step = pm.Metropolis()
    trace = pm.sample(2000,step=step)

Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, beta, alpha]
Sampling 4 chains: 100%|██████████| 10000/10000 [00:03<00:00, 2997.90draws/s]

print("alpha",trace['alpha'].shape)
print(trace['alpha'][0:5],"\n")
print("beta",trace['beta'].shape)
print(trace['beta'],"\n")
print("sigma",trace['sigma'].shape)
print(trace['sigma'])

alpha (8000,)
[1.04278775 0.88323412 0.88755258 0.87381961 0.89942359] 

beta (8000, 2)
[[1.01046211 2.55993421]
 [1.00954145 2.54110235]
 [0.91388241 2.45626273]
 ...
 [1.16787685 2.60887027]
 [0.7255497  2.42006215]
 [1.00161371 2.75913019]] 

sigma (8000,)
[0.91877597 1.17095769 0.87067159 ... 1.02761247 0.95970655 1.05418962]

可以通过 step 参数指定特定的采样器（迭代器）来替换默认的迭代器NUTS。这里给 sigma 变量指定 Slice 采样器（step），那么其他两个变量（ alpha 和 beta）的采样器会自动指定（NUTS）。

with basic_model:

    # 用MAP获得初始点
    start = pm.find_MAP(fmin=optimize.fmin_powell)

    # 实例化采样器
    step = pm.Slice(vars=[sigma])

    # 对后验分布进行5000次采样
    trace = pm.sample(5000, step=step,start=start)

/home/fjs/.local/lib/python3.5/site-packages/pymc3/tuning/starting.py:61: UserWarning: find_MAP should not be used to initialize the NUTS sampler, simply call pymc3.sample() and it will automatically initialize NUTS in a better way.
  warnings.warn('find_MAP should not be used to initialize the NUTS sampler, simply call pymc3.sample() and it will automatically initialize NUTS in a better way.')
/home/fjs/.local/lib/python3.5/site-packages/pymc3/tuning/starting.py:102: UserWarning: In future versions, set the optimization algorithm with a string. For example, use `method="L-BFGS-B"` instead of `fmin=sp.optimize.fmin_l_bfgs_b"`.
  warnings.warn('In future versions, set the optimization algorithm with a string. '
logp = -149:   5%|▌         | 269/5000 [00:00<00:01, 3256.65it/s]   
Optimization terminated successfully.
         Current function value: 148.980478
         Iterations: 6
         Function evaluations: 269
Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>Slice: [sigma]
>NUTS: [beta, alpha]
Sampling 4 chains: 100%|██████████| 22000/22000 [00:08<00:00, 2581.19draws/s]

4、后验分布分析

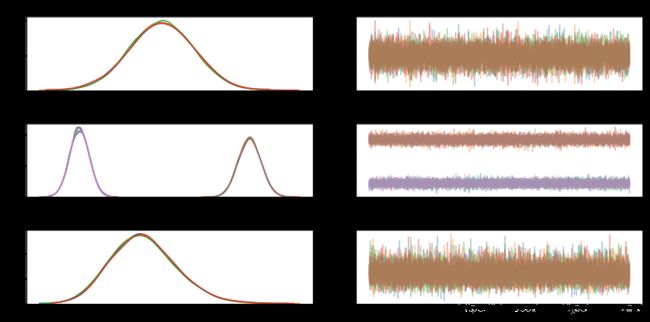
PyMC3提供了 traceplot 函数来绘制后验采样的趋势图。

pm.traceplot(trace);

左侧是每个随机变量的边际后验的直方图，使用核密度估计进行了平滑处理。右侧是马尔可夫链采样值按顺序绘制。对于向量参数 beta会有两条后验分布直方图和后验采样值。

同时也提供蚊子形式的后验统计总结，使用summary函数获得。

pm.summary(trace)

前面设置的参数如下

alpha=1
beta =[1, 2.5]
sigma=1

这里通过后验估计可以看出平均估计值：

mean(alpha)=[0.906]
mean(beta)=[0.948,2.522]
mean(sigma)=[0.991]