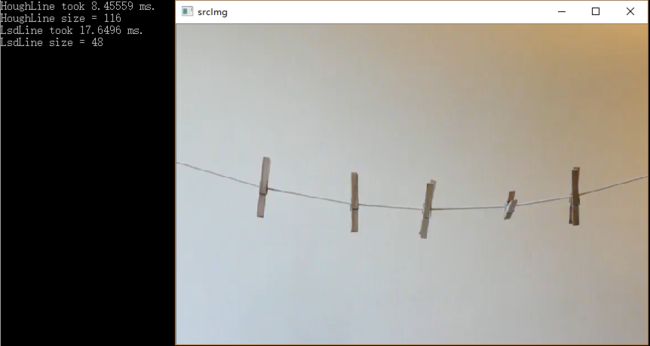
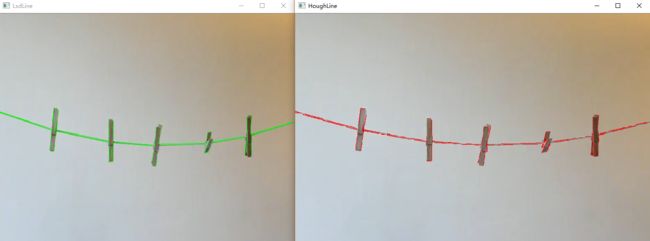
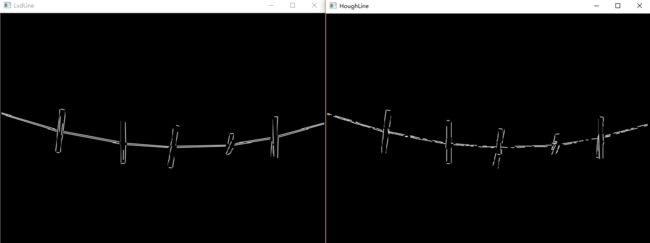
LSD直线检测
代码来源:http://www.ipol.im/pub/art/2012/gjmr-lsd/
Files
-----
README.txt - This file.
COPYING - GNU AFFERO GENERAL PUBLIC LICENSE Version 3.
Makefile - Compilation instructions for 'make'.
lsd.c - LSD module ANSI C code, peer reviewed file.
lsd.h - LSD module ANSI C header, peer reviewed file.
lsd_cmd.c - command line interface for LSD, ANSI C code.
lsd_call_example.c - Minimal example of calling LSD from a C language program.
chairs.pgm - Test image in PGM format.
chairs.lsd.txt - Expected result for 'chairs.pgm' image as an ASCII file.
chairs.lsd.eps - Expected result for 'chairs.pgm' image as an EPS file.
doc - Html code documentation.
doxygen.config - doxygen configuration file for documentation generation.
The files "lsd.c" and "lsd.h" were subject to peer review as part of
the acceptance process of the IPOL article, and are the official
version of LSD.
代码结构:
lsd.h
/*----------------------------------------------------------------------------
LSD - Line Segment Detector on digital images
Copyright 2007-2010 rafael grompone von gioi ([email protected])
This program is free software: you can redistribute it and/or modify
it under the terms of the GNU Affero General Public License as
published by the Free Software Foundation, either version 3 of the
License, or (at your option) any later version.
This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU Affero General Public License for more details.
You should have received a copy of the GNU Affero General Public License
along with this program. If not, see lsd.cpp
/*----------------------------------------------------------------------------
LSD - Line Segment Detector on digital images
Copyright 2007-2010 rafael grompone von gioi ([email protected])
This program is free software: you can redistribute it and/or modify
it under the terms of the GNU Affero General Public License as
published by the Free Software Foundation, either version 3 of the
License, or (at your option) any later version.
This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU Affero General Public License for more details.
You should have received a copy of the GNU Affero General Public License
along with this program. If not, see
#include
#include
#include
#include
#include "lsd.h"
/** ln(10) */
#ifndef M_LN10
#define M_LN10 2.30258509299404568402
#endif /* !M_LN10 */
/** PI */
#ifndef M_PI
#define M_PI 3.14159265358979323846
#endif /* !M_PI */
#ifndef FALSE
#define FALSE 0
#endif /* !FALSE */
#ifndef TRUE
#define TRUE 1
#endif /* !TRUE */
/** Label for pixels with undefined gradient. */
#define NOTDEF -1024.0
/** 3/2 pi */
#define M_3_2_PI 4.71238898038
/** 2 pi */
#define M_2__PI 6.28318530718
/** Label for pixels not used in yet. */
#define NOTUSED 0
/** Label for pixels already used in detection. */
#define USED 1
/*----------------------------------------------------------------------------*/
/** Chained list of coordinates.
*/
struct coorlist
{
int x, y;
struct coorlist *next;
};
/*----------------------------------------------------------------------------*/
/** A point (or pixel).
*/
struct point
{
int x, y;
};
/*----------------------------------------------------------------------------*/
/*------------------------- Miscellaneous functions --------------------------*/
/*----------------------------------------------------------------------------*/
/*----------------------------------------------------------------------------*/
/** Fatal error, print a message to standard-error output and exit.
*/
static void error(char *msg)
{
fprintf(stderr, "LSD Error: %s\n", msg);
exit(EXIT_FAILURE);
}
/*----------------------------------------------------------------------------*/
/** Doubles relative error factor
*/
#define RELATIVE_ERROR_FACTOR 100.0
/*----------------------------------------------------------------------------*/
/** Compare doubles by relative error.
The resulting rounding error after floating point computations
depend on the specific operations done. The same number computed by
different algorithms could present different rounding errors. For a
useful comparison, an estimation of the relative rounding error
should be considered and compared to a factor times EPS. The factor
should be related to the cumulated rounding error in the chain of
computation. Here, as a simplification, a fixed factor is used.
*/
static int double_equal(double a, double b)
{
double abs_diff, aa, bb, abs_max;
/* trivial case */
if ( a == b ) return TRUE;
abs_diff = fabs(a - b);
aa = fabs(a);
bb = fabs(b);
abs_max = aa > bb ? aa : bb;
/* DBL_MIN is the smallest normalized number, thus, the smallest
number whose relative error is bounded by DBL_EPSILON. For
smaller numbers, the same quantization steps as for DBL_MIN
are used. Then, for smaller numbers, a meaningful "relative"
error should be computed by dividing the difference by DBL_MIN. */
if ( abs_max < DBL_MIN ) abs_max = DBL_MIN;
/* equal if relative error <= factor x eps */
return (abs_diff / abs_max) <= (RELATIVE_ERROR_FACTOR * DBL_EPSILON);
}
/*----------------------------------------------------------------------------*/
/** Computes Euclidean distance between point (x1,y1) and point (x2,y2).
*/
static double dist(double x1, double y1, double x2, double y2)
{
return sqrt( (x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1) );
}
/*----------------------------------------------------------------------------*/
/*----------------------- 'list of n-tuple' data type ------------------------*/
/*----------------------------------------------------------------------------*/
/*----------------------------------------------------------------------------*/
/** Free memory used in n-tuple 'in'.
*/
void free_ntuple_list(ntuple_list in)
{
if ( in == NULL || in->values == NULL )
error("free_ntuple_list: invalid n-tuple input.");
free( (void *) in->values );
free( (void *) in );
}
/*----------------------------------------------------------------------------*/
/** Create an n-tuple list and allocate memory for one element.
@param dim the dimension (n) of the n-tuple.
*/
ntuple_list new_ntuple_list(unsigned int dim)
{
ntuple_list n_tuple;
/* check parameters */
if ( dim == 0 ) error("new_ntuple_list: 'dim' must be positive.");
/* get memory for list structure */
n_tuple = (ntuple_list) malloc( sizeof(struct ntuple_list_s) );
if ( n_tuple == NULL ) error("not enough memory.");
/* initialize list */
n_tuple->size = 0;
n_tuple->max_size = 1;
n_tuple->dim = dim;
/* get memory for tuples */
n_tuple->values = (double *) malloc( dim * n_tuple->max_size * sizeof(double) );
if ( n_tuple->values == NULL ) error("not enough memory.");
return n_tuple;
}
/*----------------------------------------------------------------------------*/
/** Enlarge the allocated memory of an n-tuple list.
*/
void enlarge_ntuple_list(ntuple_list n_tuple)
{
/* check parameters */
if ( n_tuple == NULL || n_tuple->values == NULL || n_tuple->max_size == 0 )
error("enlarge_ntuple_list: invalid n-tuple.");
/* duplicate number of tuples */
n_tuple->max_size *= 2;
/* realloc memory */
n_tuple->values = (double *) realloc( (void *) n_tuple->values,
n_tuple->dim * n_tuple->max_size * sizeof(double) );
if ( n_tuple->values == NULL ) error("not enough memory.");
}
/*----------------------------------------------------------------------------*/
/** Add a 5-tuple to an n-tuple list.
*/
void add_5tuple( ntuple_list out, double v1, double v2,
double v3, double v4, double v5 )
{
/* check parameters */
if ( out == NULL ) error("add_5tuple: invalid n-tuple input.");
if ( out->dim != 5 ) error("add_5tuple: the n-tuple must be a 5-tuple.");
/* if needed, alloc more tuples to 'out' */
if ( out->size == out->max_size ) enlarge_ntuple_list(out);
if ( out->values == NULL ) error("add_5tuple: invalid n-tuple input.");
/* add new 5-tuple */
out->values[ out->size * out->dim + 0 ] = v1;
out->values[ out->size * out->dim + 1 ] = v2;
out->values[ out->size * out->dim + 2 ] = v3;
out->values[ out->size * out->dim + 3 ] = v4;
out->values[ out->size * out->dim + 4 ] = v5;
/* update number of tuples counter */
out->size++;
}
/*----------------------------------------------------------------------------*/
/*----------------------------- Image Data Types -----------------------------*/
/*----------------------------------------------------------------------------*/
/*----------------------------------------------------------------------------*/
/** Free memory used in image_char 'i'.
*/
void free_image_char(image_char i)
{
if ( i == NULL || i->data == NULL )
error("free_image_char: invalid input image.");
free( (void *) i->data );
free( (void *) i );
}
/*----------------------------------------------------------------------------*/
/** Create a new image_char of size 'xsize' times 'ysize'.
*/
image_char new_image_char(unsigned int xsize, unsigned int ysize)
{
image_char image;
/* check parameters */
if ( xsize == 0 || ysize == 0 ) error("new_image_char: invalid image size.");
/* get memory */
image = (image_char) malloc( sizeof(struct image_char_s) );
if ( image == NULL ) error("not enough memory.");
image->data = (unsigned char *) calloc( (size_t) (xsize * ysize),
sizeof(unsigned char) );
if ( image->data == NULL ) error("not enough memory.");
/* set image size */
image->xsize = xsize;
image->ysize = ysize;
return image;
}
/*----------------------------------------------------------------------------*/
/** Create a new image_char of size 'xsize' times 'ysize',
initialized to the value 'fill_value'.
*/
image_char new_image_char_ini( unsigned int xsize, unsigned int ysize,
unsigned char fill_value )
{
image_char image = new_image_char(xsize, ysize); /* create image */
unsigned int N = xsize * ysize;
unsigned int i;
/* check parameters */
if ( image == NULL || image->data == NULL )
error("new_image_char_ini: invalid image.");
/* initialize */
for (i = 0; i < N; i++) image->data[i] = fill_value;
return image;
}
/*----------------------------------------------------------------------------*/
/** Free memory used in image_int 'i'.
*/
void free_image_int(image_int i)
{
if ( i == NULL || i->data == NULL )
error("free_image_int: invalid input image.");
free( (void *) i->data );
free( (void *) i );
}
/*----------------------------------------------------------------------------*/
/** Create a new image_int of size 'xsize' times 'ysize'.
*/
image_int new_image_int(unsigned int xsize, unsigned int ysize)
{
image_int image;
/* check parameters */
if ( xsize == 0 || ysize == 0 ) error("new_image_int: invalid image size.");
/* get memory */
image = (image_int) malloc( sizeof(struct image_int_s) );
if ( image == NULL ) error("not enough memory.");
image->data = (int *) calloc( (size_t) (xsize * ysize), sizeof(int) );
if ( image->data == NULL ) error("not enough memory.");
/* set image size */
image->xsize = xsize;
image->ysize = ysize;
return image;
}
/*----------------------------------------------------------------------------*/
/** Create a new image_int of size 'xsize' times 'ysize',
initialized to the value 'fill_value'.
*/
image_int new_image_int_ini( unsigned int xsize, unsigned int ysize,
int fill_value )
{
image_int image = new_image_int(xsize, ysize); /* create image */
unsigned int N = xsize * ysize;
unsigned int i;
/* initialize */
for (i = 0; i < N; i++) image->data[i] = fill_value;
return image;
}
/*----------------------------------------------------------------------------*/
/** Free memory used in image_double 'i'.
*/
void free_image_double(image_double i)
{
if ( i == NULL || i->data == NULL )
error("free_image_double: invalid input image.");
free( (void *) i->data );
free( (void *) i );
}
/*----------------------------------------------------------------------------*/
/** Create a new image_double of size 'xsize' times 'ysize'.
*/
image_double new_image_double(unsigned int xsize, unsigned int ysize)
{
image_double image;
/* check parameters */
if ( xsize == 0 || ysize == 0 ) error("new_image_double: invalid image size.");
/* get memory */
image = (image_double) malloc( sizeof(struct image_double_s) );
if ( image == NULL ) error("not enough memory.");
image->data = (double *) calloc( (size_t) (xsize * ysize), sizeof(double) );
if ( image->data == NULL ) error("not enough memory.");
/* set image size */
image->xsize = xsize;
image->ysize = ysize;
return image;
}
/*----------------------------------------------------------------------------*/
/** Create a new image_double of size 'xsize' times 'ysize',
initialized to the value 'fill_value'.
*/
image_double new_image_double_ini( unsigned int xsize, unsigned int ysize,
double fill_value )
{
image_double image = new_image_double(xsize, ysize); /* create image */
unsigned int N = xsize * ysize;
unsigned int i;
/* initialize */
for (i = 0; i < N; i++) image->data[i] = fill_value;
return image;
}
/*----------------------------------------------------------------------------*/
/*----------------------------- Gaussian filter ------------------------------*/
/*----------------------------------------------------------------------------*/
/*----------------------------------------------------------------------------*/
/** Compute a Gaussian kernel of length 'kernel->dim',
standard deviation 'sigma', and centered at value 'mean'.
For example, if mean=0.5, the Gaussian will be centered
in the middle point between values 'kernel->values[0]'
and 'kernel->values[1]'.
*/
static void gaussian_kernel(ntuple_list kernel, double sigma, double mean)
{
double sum = 0.0;
double val;
unsigned int i;
/* check parameters */
if ( kernel == NULL || kernel->values == NULL )
error("gaussian_kernel: invalid n-tuple 'kernel'.");
if ( sigma <= 0.0 ) error("gaussian_kernel: 'sigma' must be positive.");
/* compute Gaussian kernel */
if ( kernel->max_size < 1 ) enlarge_ntuple_list(kernel);
kernel->size = 1;
for (i = 0; i < kernel->dim; i++)
{
val = ( (double) i - mean ) / sigma;
kernel->values[i] = exp( -0.5 * val * val );
sum += kernel->values[i];
}
/* normalization */
if ( sum >= 0.0 ) for (i = 0; i < kernel->dim; i++) kernel->values[i] /= sum;
}
/*----------------------------------------------------------------------------*/
/** Scale the input image 'in' by a factor 'scale' by Gaussian sub-sampling.
For example, scale=0.8 will give a result at 80% of the original size.
The image is convolved with a Gaussian kernel
@f[
G(x,y) = \frac{1}{2\pi\sigma^2} e^{-\frac{x^2+y^2}{2\sigma^2}}
@f]
before the sub-sampling to prevent aliasing.
The standard deviation sigma given by:
- sigma = sigma_scale / scale, if scale < 1.0
- sigma = sigma_scale, if scale >= 1.0
To be able to sub-sample at non-integer steps, some interpolation
is needed. In this implementation, the interpolation is done by
the Gaussian kernel, so both operations (filtering and sampling)
are done at the same time. The Gaussian kernel is computed
centered on the coordinates of the required sample. In this way,
when applied, it gives directly the result of convolving the image
with the kernel and interpolated to that particular position.
A fast algorithm is done using the separability of the Gaussian
kernel. Applying the 2D Gaussian kernel is equivalent to applying
first a horizontal 1D Gaussian kernel and then a vertical 1D
Gaussian kernel (or the other way round). The reason is that
@f[
G(x,y) = G(x) * G(y)
@f]
where
@f[
G(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{x^2}{2\sigma^2}}.
@f]
The algorithm first apply a combined Gaussian kernel and sampling
in the x axis, and then the combined Gaussian kernel and sampling
in the y axis.
*/
static image_double gaussian_sampler( image_double in, double scale,
double sigma_scale )
{
image_double aux, out;
ntuple_list kernel;
unsigned int N, M, h, n, x, y, i;
int xc, yc, j, double_x_size, double_y_size;
double sigma, xx, yy, sum, prec;
/* check parameters */
if ( in == NULL || in->data == NULL || in->xsize == 0 || in->ysize == 0 )
error("gaussian_sampler: invalid image.");
if ( scale <= 0.0 ) error("gaussian_sampler: 'scale' must be positive.");
if ( sigma_scale <= 0.0 )
error("gaussian_sampler: 'sigma_scale' must be positive.");
/* get memory for images */
if ( in->xsize * scale > (double) UINT_MAX ||
in->ysize * scale > (double) UINT_MAX )
error("gaussian_sampler: the output image size exceeds the handled size.");
N = (unsigned int) floor( in->xsize * scale );
M = (unsigned int) floor( in->ysize * scale );
aux = new_image_double(N, in->ysize);
out = new_image_double(N, M);
/* sigma, kernel size and memory for the kernel */
sigma = scale < 1.0 ? sigma_scale / scale : sigma_scale;
/*
The size of the kernel is selected to guarantee that the
the first discarded term is at least 10^prec times smaller
than the central value. For that, h should be larger than x, with
e^(-x^2/2sigma^2) = 1/10^prec.
Then,
x = sigma * sqrt( 2 * prec * ln(10) ).
*/
prec = 3.0;
h = (unsigned int) ceil( sigma * sqrt( 2.0 * prec * log(10.0) ) );
n = 1 + 2 * h; /* kernel size */
kernel = new_ntuple_list(n);
/* auxiliary double image size variables */
double_x_size = (int) (2 * in->xsize);
double_y_size = (int) (2 * in->ysize);
/* First subsampling: x axis */
for (x = 0; x < aux->xsize; x++)
{
/*
x is the coordinate in the new image.
xx is the corresponding x-value in the original size image.
xc is the integer value, the pixel coordinate of xx.
*/
xx = (double) x / scale;
/* coordinate (0.0,0.0) is in the center of pixel (0,0),
so the pixel with xc=0 get the values of xx from -0.5 to 0.5 */
xc = (int) floor( xx + 0.5 );
gaussian_kernel( kernel, sigma, (double) h + xx - (double) xc );
/* the kernel must be computed for each x because the fine
offset xx-xc is different in each case */
for (y = 0; y < aux->ysize; y++)
{
sum = 0.0;
for (i = 0; i < kernel->dim; i++)
{
j = xc - h + i;
/* symmetry boundary condition */
while ( j < 0 ) j += double_x_size;
while ( j >= double_x_size ) j -= double_x_size;
if ( j >= (int) in->xsize ) j = double_x_size - 1 - j;
sum += in->data[ j + y * in->xsize ] * kernel->values[i];
}
aux->data[ x + y * aux->xsize ] = sum;
}
}
/* Second subsampling: y axis */
for (y = 0; y < out->ysize; y++)
{
/*
y is the coordinate in the new image.
yy is the corresponding x-value in the original size image.
yc is the integer value, the pixel coordinate of xx.
*/
yy = (double) y / scale;
/* coordinate (0.0,0.0) is in the center of pixel (0,0),
so the pixel with yc=0 get the values of yy from -0.5 to 0.5 */
yc = (int) floor( yy + 0.5 );
gaussian_kernel( kernel, sigma, (double) h + yy - (double) yc );
/* the kernel must be computed for each y because the fine
offset yy-yc is different in each case */
for (x = 0; x < out->xsize; x++)
{
sum = 0.0;
for (i = 0; i < kernel->dim; i++)
{
j = yc - h + i;
/* symmetry boundary condition */
while ( j < 0 ) j += double_y_size;
while ( j >= double_y_size ) j -= double_y_size;
if ( j >= (int) in->ysize ) j = double_y_size - 1 - j;
sum += aux->data[ x + j * aux->xsize ] * kernel->values[i];
}
out->data[ x + y * out->xsize ] = sum;
}
}
/* free memory */
free_ntuple_list(kernel);
free_image_double(aux);
return out;
}
/*----------------------------------------------------------------------------*/
/*--------------------------------- Gradient ---------------------------------*/
/*----------------------------------------------------------------------------*/
/*----------------------------------------------------------------------------*/
/** Computes the direction of the level line of 'in' at each point.
The result is:
- an image_double with the angle at each pixel, or NOTDEF if not defined.
- the image_double 'modgrad' (a pointer is passed as argument)
with the gradient magnitude at each point.
- a list of pixels 'list_p' roughly ordered by decreasing
gradient magnitude. (The order is made by classifying points
into bins by gradient magnitude. The parameters 'n_bins' and
'max_grad' specify the number of bins and the gradient modulus
at the highest bin. The pixels in the list would be in
decreasing gradient magnitude, up to a precision of the size of
the bins.)
- a pointer 'mem_p' to the memory used by 'list_p' to be able to
free the memory when it is not used anymore.
*/
static image_double ll_angle( image_double in, double threshold,
struct coorlist **list_p, void **mem_p,
image_double *modgrad, unsigned int n_bins,
double max_grad )
{
image_double g;
unsigned int n, p, x, y, adr, i;
double com1, com2, gx, gy, norm, norm2;
/* the rest of the variables are used for pseudo-ordering
the gradient magnitude values */
int list_count = 0;
struct coorlist *list;
struct coorlist **range_l_s; /* array of pointers to start of bin list */
struct coorlist **range_l_e; /* array of pointers to end of bin list */
struct coorlist *start;
struct coorlist *end;
/* check parameters */
if ( in == NULL || in->data == NULL || in->xsize == 0 || in->ysize == 0 )
error("ll_angle: invalid image.");
if ( threshold < 0.0 ) error("ll_angle: 'threshold' must be positive.");
if ( list_p == NULL ) error("ll_angle: NULL pointer 'list_p'.");
if ( mem_p == NULL ) error("ll_angle: NULL pointer 'mem_p'.");
if ( modgrad == NULL ) error("ll_angle: NULL pointer 'modgrad'.");
if ( n_bins == 0 ) error("ll_angle: 'n_bins' must be positive.");
if ( max_grad <= 0.0 ) error("ll_angle: 'max_grad' must be positive.");
/* image size shortcuts */
n = in->ysize;
p = in->xsize;
/* allocate output image */
g = new_image_double(in->xsize, in->ysize);
/* get memory for the image of gradient modulus */
*modgrad = new_image_double(in->xsize, in->ysize);
/* get memory for "ordered" list of pixels */
list = (struct coorlist *) calloc( (size_t) (n * p), sizeof(struct coorlist) );
*mem_p = (void *) list;
range_l_s = (struct coorlist **) calloc( (size_t) n_bins,
sizeof(struct coorlist *) );
range_l_e = (struct coorlist **) calloc( (size_t) n_bins,
sizeof(struct coorlist *) );
if ( list == NULL || range_l_s == NULL || range_l_e == NULL )
error("not enough memory.");
for (i = 0; i < n_bins; i++) range_l_s[i] = range_l_e[i] = NULL;
/* 'undefined' on the down and right boundaries */
for (x = 0; x < p; x++) g->data[(n - 1)*p + x] = NOTDEF;
for (y = 0; y < n; y++) g->data[p * y + p - 1] = NOTDEF;
/* compute gradient on the remaining pixels */
for (x = 0; x < p - 1; x++)
for (y = 0; y < n - 1; y++)
{
adr = y * p + x;
/*
Norm 2 computation using 2x2 pixel window:
A B
C D
and
com1 = D-A, com2 = B-C.
Then
gx = B+D - (A+C) horizontal difference
gy = C+D - (A+B) vertical difference
com1 and com2 are just to avoid 2 additions.
*/
com1 = in->data[adr + p + 1] - in->data[adr];
com2 = in->data[adr + 1] - in->data[adr + p];
gx = com1 + com2; /* gradient x component */
gy = com1 - com2; /* gradient y component */
norm2 = gx * gx + gy * gy;
norm = sqrt( norm2 / 4.0 ); /* gradient norm */
(*modgrad)->data[adr] = norm; /* store gradient norm */
if ( norm <= threshold ) /* norm too small, gradient no defined */
g->data[adr] = NOTDEF; /* gradient angle not defined */
else
{
/* gradient angle computation */
g->data[adr] = atan2(gx, -gy);
/* store the point in the right bin according to its norm */
i = (unsigned int) (norm * (double) n_bins / max_grad);
if ( i >= n_bins ) i = n_bins - 1;
if ( range_l_e[i] == NULL )
range_l_s[i] = range_l_e[i] = list + list_count++;
else
{
range_l_e[i]->next = list + list_count;
range_l_e[i] = list + list_count++;
}
range_l_e[i]->x = (int) x;
range_l_e[i]->y = (int) y;
range_l_e[i]->next = NULL;
}
}
/* Make the list of pixels (almost) ordered by norm value.
It starts by the larger bin, so the list starts by the
pixels with higher gradient value. Pixels would be ordered
by norm value, up to a precision given by max_grad/n_bins.
*/
for (i = n_bins - 1; i > 0 && range_l_s[i] == NULL; i--);
start = range_l_s[i];
end = range_l_e[i];
if ( start != NULL )
for (i--; i > 0; i--)
if ( range_l_s[i] != NULL )
{
end->next = range_l_s[i];
end = range_l_e[i];
}
*list_p = start;
/* free memory */
free( (void *) range_l_s );
free( (void *) range_l_e );
return g;
}
/*----------------------------------------------------------------------------*/
/** Is point (x,y) aligned to angle theta, up to precision 'prec'?
*/
static int isaligned( int x, int y, image_double angles, double theta,
double prec )
{
double a;
/* check parameters */
if ( angles == NULL || angles->data == NULL )
error("isaligned: invalid image 'angles'.");
if ( x < 0 || y < 0 || x >= (int) angles->xsize || y >= (int) angles->ysize )
error("isaligned: (x,y) out of the image.");
if ( prec < 0.0 ) error("isaligned: 'prec' must be positive.");
/* angle at pixel (x,y) */
a = angles->data[ x + y * angles->xsize ];
/* pixels whose level-line angle is not defined
are considered as NON-aligned */
if ( a == NOTDEF ) return FALSE; /* there is no need to call the function
'double_equal' here because there is
no risk of problems related to the
comparison doubles, we are only
interested in the exact NOTDEF value */
/* it is assumed that 'theta' and 'a' are in the range [-pi,pi] */
theta -= a;
if ( theta < 0.0 ) theta = -theta;
if ( theta > M_3_2_PI )
{
theta -= M_2__PI;
if ( theta < 0.0 ) theta = -theta;
}
return theta < prec;
}
/*----------------------------------------------------------------------------*/
/** Absolute value angle difference.
*/
static double angle_diff(double a, double b)
{
a -= b;
while ( a <= -M_PI ) a += M_2__PI;
while ( a > M_PI ) a -= M_2__PI;
if ( a < 0.0 ) a = -a;
return a;
}
/*----------------------------------------------------------------------------*/
/** Signed angle difference.
*/
static double angle_diff_signed(double a, double b)
{
a -= b;
while ( a <= -M_PI ) a += M_2__PI;
while ( a > M_PI ) a -= M_2__PI;
return a;
}
/*----------------------------------------------------------------------------*/
/*----------------------------- NFA computation ------------------------------*/
/*----------------------------------------------------------------------------*/
/*----------------------------------------------------------------------------*/
/** Computes the natural logarithm of the absolute value of
the gamma function of x using the Lanczos approximation.
See http://www.rskey.org/gamma.htm
The formula used is
@f[
\Gamma(x) = \frac{ \sum_{n=0}^{N} q_n x^n }{ \Pi_{n=0}^{N} (x+n) }
(x+5.5)^{x+0.5} e^{-(x+5.5)}
@f]
so
@f[
\log\Gamma(x) = \log\left( \sum_{n=0}^{N} q_n x^n \right)
+ (x+0.5) \log(x+5.5) - (x+5.5) - \sum_{n=0}^{N} \log(x+n)
@f]
and
q0 = 75122.6331530,
q1 = 80916.6278952,
q2 = 36308.2951477,
q3 = 8687.24529705,
q4 = 1168.92649479,
q5 = 83.8676043424,
q6 = 2.50662827511.
*/
static double log_gamma_lanczos(double x)
{
static double q[7] = { 75122.6331530, 80916.6278952, 36308.2951477,
8687.24529705, 1168.92649479, 83.8676043424,
2.50662827511
};
double a = (x + 0.5) * log(x + 5.5) - (x + 5.5);
double b = 0.0;
int n;
for (n = 0; n < 7; n++)
{
a -= log( x + (double) n );
b += q[n] * pow( x, (double) n );
}
return a + log(b);
}
/*----------------------------------------------------------------------------*/
/** Computes the natural logarithm of the absolute value of
the gamma function of x using Windschitl method.
See http://www.rskey.org/gamma.htm
The formula used is
@f[
\Gamma(x) = \sqrt{\frac{2\pi}{x}} \left( \frac{x}{e}
\sqrt{ x\sinh(1/x) + \frac{1}{810x^6} } \right)^x
@f]
so
@f[
\log\Gamma(x) = 0.5\log(2\pi) + (x-0.5)\log(x) - x
+ 0.5x\log\left( x\sinh(1/x) + \frac{1}{810x^6} \right).
@f]
This formula is a good approximation when x > 15.
*/
static double log_gamma_windschitl(double x)
{
return 0.918938533204673 + (x - 0.5) * log(x) - x
+ 0.5 * x * log( x * sinh(1 / x) + 1 / (810.0 * pow(x, 6.0)) );
}
/*----------------------------------------------------------------------------*/
/** Computes the natural logarithm of the absolute value of
the gamma function of x. When x>15 use log_gamma_windschitl(),
otherwise use log_gamma_lanczos().
*/
#define log_gamma(x) ((x)>15.0?log_gamma_windschitl(x):log_gamma_lanczos(x))
/*----------------------------------------------------------------------------*/
/** Size of the table to store already computed inverse values.
*/
#define TABSIZE 100000
/*----------------------------------------------------------------------------*/
/** Computes -log10(NFA).
NFA stands for Number of False Alarms:
@f[
\mathrm{NFA} = NT \cdot B(n,k,p)
@f]
- NT - number of tests
- B(n,k,p) - tail of binomial distribution with parameters n,k and p:
@f[
B(n,k,p) = \sum_{j=k}^n
\left(\begin{array}{c}n\\j\end{array}\right)
p^{j} (1-p)^{n-j}
@f]
The value -log10(NFA) is equivalent but more intuitive than NFA:
- -1 corresponds to 10 mean false alarms
- 0 corresponds to 1 mean false alarm
- 1 corresponds to 0.1 mean false alarms
- 2 corresponds to 0.01 mean false alarms
- ...
Used this way, the bigger the value, better the detection,
and a logarithmic scale is used.
@param n,k,p binomial parameters.
@param logNT logarithm of Number of Tests
The computation is based in the gamma function by the following
relation:
@f[
\left(\begin{array}{c}n\\k\end{array}\right)
= \frac{ \Gamma(n+1) }{ \Gamma(k+1) \cdot \Gamma(n-k+1) }.
@f]
We use efficient algorithms to compute the logarithm of
the gamma function.
To make the computation faster, not all the sum is computed, part
of the terms are neglected based on a bound to the error obtained
(an error of 10% in the result is accepted).
*/
static double nfa(int n, int k, double p, double logNT)
{
static double inv[TABSIZE]; /* table to keep computed inverse values */
double tolerance = 0.1; /* an error of 10% in the result is accepted */
double log1term, term, bin_term, mult_term, bin_tail, err, p_term;
int i;
/* check parameters */
if ( n < 0 || k < 0 || k > n || p <= 0.0 || p >= 1.0 )
error("nfa: wrong n, k or p values.");
/* trivial cases */
if ( n == 0 || k == 0 ) return -logNT;
if ( n == k ) return -logNT - (double) n * log10(p);
/* probability term */
p_term = p / (1.0 - p);
/* compute the first term of the series */
/*
binomial_tail(n,k,p) = sum_{i=k}^n bincoef(n,i) * p^i * (1-p)^{n-i}
where bincoef(n,i) are the binomial coefficients.
But
bincoef(n,k) = gamma(n+1) / ( gamma(k+1) * gamma(n-k+1) ).
We use this to compute the first term. Actually the log of it.
*/
log1term = log_gamma( (double) n + 1.0 ) - log_gamma( (double) k + 1.0 )
- log_gamma( (double) (n - k) + 1.0 )
+ (double) k * log(p) + (double) (n - k) * log(1.0 - p);
term = exp(log1term);
/* in some cases no more computations are needed */
if ( double_equal(term, 0.0) ) /* the first term is almost zero */
{
if ( (double) k > (double) n * p ) /* at begin or end of the tail? */
return -log1term / M_LN10 - logNT; /* end: use just the first term */
else
return -logNT; /* begin: the tail is roughly 1 */
}
/* compute more terms if needed */
bin_tail = term;
for (i = k + 1; i <= n; i++)
{
/*
As
term_i = bincoef(n,i) * p^i * (1-p)^(n-i)
and
bincoef(n,i)/bincoef(n,i-1) = n-1+1 / i,
then,
term_i / term_i-1 = (n-i+1)/i * p/(1-p)
and
term_i = term_i-1 * (n-i+1)/i * p/(1-p).
1/i is stored in a table as they are computed,
because divisions are expensive.
p/(1-p) is computed only once and stored in 'p_term'.
*/
bin_term = (double) (n - i + 1) * ( i < TABSIZE ?
( inv[i] != 0.0 ? inv[i] : ( inv[i] = 1.0 / (double) i ) ) :
1.0 / (double) i );
mult_term = bin_term * p_term;
term *= mult_term;
bin_tail += term;
if (bin_term < 1.0)
{
/* When bin_term<1 then mult_term_ji.
Then, the error on the binomial tail when truncated at
the i term can be bounded by a geometric series of form
term_i * sum mult_term_i^j. */
err = term * ( ( 1.0 - pow( mult_term, (double) (n - i + 1) ) ) /
(1.0 - mult_term) - 1.0 );
/* One wants an error at most of tolerance*final_result, or:
tolerance * abs(-log10(bin_tail)-logNT).
Now, the error that can be accepted on bin_tail is
given by tolerance*final_result divided by the derivative
of -log10(x) when x=bin_tail. that is:
tolerance * abs(-log10(bin_tail)-logNT) / (1/bin_tail)
Finally, we truncate the tail if the error is less than:
tolerance * abs(-log10(bin_tail)-logNT) * bin_tail */
if ( err < tolerance * fabs(-log10(bin_tail) - logNT) * bin_tail ) break;
}
}
return -log10(bin_tail) - logNT;
}
/*----------------------------------------------------------------------------*/
/*--------------------------- Rectangle structure ----------------------------*/
/*----------------------------------------------------------------------------*/
/*----------------------------------------------------------------------------*/
/** Rectangle structure: line segment with width.
*/
struct rect
{
double x1, y1, x2, y2; /* first and second point of the line segment */
double width; /* rectangle width */
double x, y; /* center of the rectangle */
double theta; /* angle */
double dx, dy; /* vector with the line segment angle */
double prec; /* tolerance angle */
double p; /* probability of a point with angle within 'prec' */
};
/*----------------------------------------------------------------------------*/
/** Copy one rectangle structure to another.
*/
static void rect_copy(struct rect *in, struct rect *out)
{
/* check parameters */
if ( in == NULL || out == NULL ) error("rect_copy: invalid 'in' or 'out'.");
/* copy values */
out->x1 = in->x1;
out->y1 = in->y1;
out->x2 = in->x2;
out->y2 = in->y2;
out->width = in->width;
out->x = in->x;
out->y = in->y;
out->theta = in->theta;
out->dx = in->dx;
out->dy = in->dy;
out->prec = in->prec;
out->p = in->p;
}
/*----------------------------------------------------------------------------*/
/** Rectangle points iterator.
The integer coordinates of pixels inside a rectangle are
iteratively explored. This structure keep track of the process and
functions ri_ini(), ri_inc(), ri_end(), and ri_del() are used in
the process. An example of how to use the iterator is as follows:
\code
struct rect * rec = XXX; // some rectangle
rect_iter * i;
for( i=ri_ini(rec); !ri_end(i); ri_inc(i) )
{
// your code, using 'i->x' and 'i->y' as coordinates
}
ri_del(i); // delete iterator
\endcode
The pixels are explored 'column' by 'column', where we call
'column' a set of pixels with the same x value that are inside the
rectangle. The following is an schematic representation of a
rectangle, the 'column' being explored is marked by colons, and
the current pixel being explored is 'x,y'.
\verbatim
vx[1],vy[1]
* *
* *
* *
* ye
* : *
vx[0],vy[0] : *
* : *
* x,y *
* : *
* : vx[2],vy[2]
* : *
y ys *
^ * *
| * *
| * *
+---> x vx[3],vy[3]
\endverbatim
The first 'column' to be explored is the one with the smaller x
value. Each 'column' is explored starting from the pixel of the
'column' (inside the rectangle) with the smaller y value.
The four corners of the rectangle are stored in order that rotates
around the corners at the arrays 'vx[]' and 'vy[]'. The first
point is always the one with smaller x value.
'x' and 'y' are the coordinates of the pixel being explored. 'ys'
and 'ye' are the start and end values of the current column being
explored. So, 'ys' < 'ye'.
*/
typedef struct
{
double vx[4]; /* rectangle's corner X coordinates in circular order */
double vy[4]; /* rectangle's corner Y coordinates in circular order */
double ys, ye; /* start and end Y values of current 'column' */
int x, y; /* coordinates of currently explored pixel */
} rect_iter;
/*----------------------------------------------------------------------------*/
/** Interpolate y value corresponding to 'x' value given, in
the line 'x1,y1' to 'x2,y2'; if 'x1=x2' return the smaller
of 'y1' and 'y2'.
The following restrictions are required:
- x1 <= x2
- x1 <= x
- x <= x2
*/
static double inter_low(double x, double x1, double y1, double x2, double y2)
{
/* check parameters */
if ( x1 > x2 || x < x1 || x > x2 )
error("inter_low: unsuitable input, 'x1>x2' or 'xx2'.");
/* interpolation */
if ( double_equal(x1, x2) && y1 < y2 ) return y1;
if ( double_equal(x1, x2) && y1 > y2 ) return y2;
return y1 + (x - x1) * (y2 - y1) / (x2 - x1);
}
/*----------------------------------------------------------------------------*/
/** Interpolate y value corresponding to 'x' value given, in
the line 'x1,y1' to 'x2,y2'; if 'x1=x2' return the larger
of 'y1' and 'y2'.
The following restrictions are required:
- x1 <= x2
- x1 <= x
- x <= x2
*/
static double inter_hi(double x, double x1, double y1, double x2, double y2)
{
/* check parameters */
if ( x1 > x2 || x < x1 || x > x2 )
error("inter_hi: unsuitable input, 'x1>x2' or 'xx2'.");
/* interpolation */
if ( double_equal(x1, x2) && y1 < y2 ) return y2;
if ( double_equal(x1, x2) && y1 > y2 ) return y1;
return y1 + (x - x1) * (y2 - y1) / (x2 - x1);
}
/*----------------------------------------------------------------------------*/
/** Free memory used by a rectangle iterator.
*/
static void ri_del(rect_iter *iter)
{
if ( iter == NULL ) error("ri_del: NULL iterator.");
free( (void *) iter );
}
/*----------------------------------------------------------------------------*/
/** Check if the iterator finished the full iteration.
See details in \ref rect_iter
*/
static int ri_end(rect_iter *i)
{
/* check input */
if ( i == NULL ) error("ri_end: NULL iterator.");
/* if the current x value is larger than the larger
x value in the rectangle (vx[2]), we know the full
exploration of the rectangle is finished. */
return (double)(i->x) > i->vx[2];
}
/*----------------------------------------------------------------------------*/
/** Increment a rectangle iterator.
See details in \ref rect_iter
*/
static void ri_inc(rect_iter *i)
{
/* check input */
if ( i == NULL ) error("ri_inc: NULL iterator.");
/* if not at end of exploration,
increase y value for next pixel in the 'column' */
if ( !ri_end(i) ) i->y++;
/* if the end of the current 'column' is reached,
and it is not the end of exploration,
advance to the next 'column' */
while ( (double) (i->y) > i->ye && !ri_end(i) )
{
/* increase x, next 'column' */
i->x++;
/* if end of exploration, return */
if ( ri_end(i) ) return;
/* update lower y limit (start) for the new 'column'.
We need to interpolate the y value that corresponds to the
lower side of the rectangle. The first thing is to decide if
the corresponding side is
vx[0],vy[0] to vx[3],vy[3] or
vx[3],vy[3] to vx[2],vy[2]
Then, the side is interpolated for the x value of the
'column'. But, if the side is vertical (as it could happen if
the rectangle is vertical and we are dealing with the first
or last 'columns') then we pick the lower value of the side
by using 'inter_low'.
*/
if ( (double) i->x < i->vx[3] )
i->ys = inter_low((double)i->x, i->vx[0], i->vy[0], i->vx[3], i->vy[3]);
else
i->ys = inter_low((double)i->x, i->vx[3], i->vy[3], i->vx[2], i->vy[2]);
/* update upper y limit (end) for the new 'column'.
We need to interpolate the y value that corresponds to the
upper side of the rectangle. The first thing is to decide if
the corresponding side is
vx[0],vy[0] to vx[1],vy[1] or
vx[1],vy[1] to vx[2],vy[2]
Then, the side is interpolated for the x value of the
'column'. But, if the side is vertical (as it could happen if
the rectangle is vertical and we are dealing with the first
or last 'columns') then we pick the lower value of the side
by using 'inter_low'.
*/
if ( (double)i->x < i->vx[1] )
i->ye = inter_hi((double)i->x, i->vx[0], i->vy[0], i->vx[1], i->vy[1]);
else
i->ye = inter_hi((double)i->x, i->vx[1], i->vy[1], i->vx[2], i->vy[2]);
/* new y */
i->y = (int) ceil(i->ys);
}
}
/*----------------------------------------------------------------------------*/
/** Create and initialize a rectangle iterator.
See details in \ref rect_iter
*/
static rect_iter *ri_ini(struct rect *r)
{
double vx[4], vy[4];
int n, offset;
rect_iter *i;
/* check parameters */
if ( r == NULL ) error("ri_ini: invalid rectangle.");
/* get memory */
i = (rect_iter *) malloc(sizeof(rect_iter));
if ( i == NULL ) error("ri_ini: Not enough memory.");
/* build list of rectangle corners ordered
in a circular way around the rectangle */
vx[0] = r->x1 - r->dy * r->width / 2.0;
vy[0] = r->y1 + r->dx * r->width / 2.0;
vx[1] = r->x2 - r->dy * r->width / 2.0;
vy[1] = r->y2 + r->dx * r->width / 2.0;
vx[2] = r->x2 + r->dy * r->width / 2.0;
vy[2] = r->y2 - r->dx * r->width / 2.0;
vx[3] = r->x1 + r->dy * r->width / 2.0;
vy[3] = r->y1 - r->dx * r->width / 2.0;
/* compute rotation of index of corners needed so that the first
point has the smaller x.
if one side is vertical, thus two corners have the same smaller x
value, the one with the largest y value is selected as the first.
*/
if ( r->x1 < r->x2 && r->y1 <= r->y2 ) offset = 0;
else if ( r->x1 >= r->x2 && r->y1 < r->y2 ) offset = 1;
else if ( r->x1 > r->x2 && r->y1 >= r->y2 ) offset = 2;
else offset = 3;
/* apply rotation of index. */
for (n = 0; n < 4; n++)
{
i->vx[n] = vx[(offset + n) % 4];
i->vy[n] = vy[(offset + n) % 4];
}
/* Set a initial condition.
The values are set to values that will cause 'ri_inc' (that will
be called immediately) to initialize correctly the first 'column'
and compute the limits 'ys' and 'ye'.
'y' is set to the integer value of vy[0], the starting corner.
'ys' and 'ye' are set to very small values, so 'ri_inc' will
notice that it needs to start a new 'column'.
The smaller integer coordinate inside of the rectangle is
'ceil(vx[0])'. The current 'x' value is set to that value minus
one, so 'ri_inc' (that will increase x by one) will advance to
the first 'column'.
*/
i->x = (int) ceil(i->vx[0]) - 1;
i->y = (int) ceil(i->vy[0]);
i->ys = i->ye = -DBL_MAX;
/* advance to the first pixel */
ri_inc(i);
return i;
}
/*----------------------------------------------------------------------------*/
/** Compute a rectangle's NFA value.
*/
static double rect_nfa(struct rect *rec, image_double angles, double logNT)
{
rect_iter *i;
int pts = 0;
int alg = 0;
/* check parameters */
if ( rec == NULL ) error("rect_nfa: invalid rectangle.");
if ( angles == NULL ) error("rect_nfa: invalid 'angles'.");
/* compute the total number of pixels and of aligned points in 'rec' */
for (i = ri_ini(rec); !ri_end(i); ri_inc(i)) /* rectangle iterator */
if ( i->x >= 0 && i->y >= 0 &&
i->x < (int) angles->xsize && i->y < (int) angles->ysize )
{
++pts; /* total number of pixels counter */
if ( isaligned(i->x, i->y, angles, rec->theta, rec->prec) )
++alg; /* aligned points counter */
}
ri_del(i); /* delete iterator */
return nfa(pts, alg, rec->p, logNT); /* compute NFA value */
}
/*----------------------------------------------------------------------------*/
/*---------------------------------- Regions ---------------------------------*/
/*----------------------------------------------------------------------------*/
/*----------------------------------------------------------------------------*/
/** Compute region's angle as the principal inertia axis of the region.
The following is the region inertia matrix A:
@f[
A = \left(\begin{array}{cc}
Ixx & Ixy \\
Ixy & Iyy \\
\end{array}\right)
@f]
where
Ixx = sum_i G(i).(y_i - cx)^2
Iyy = sum_i G(i).(x_i - cy)^2
Ixy = - sum_i G(i).(x_i - cx).(y_i - cy)
and
- G(i) is the gradient norm at pixel i, used as pixel's weight.
- x_i and y_i are the coordinates of pixel i.
- cx and cy are the coordinates of the center of th region.
lambda1 and lambda2 are the eigenvalues of matrix A,
with lambda1 >= lambda2. They are found by solving the
characteristic polynomial:
det( lambda I - A) = 0
that gives:
lambda1 = ( Ixx + Iyy + sqrt( (Ixx-Iyy)^2 + 4.0*Ixy*Ixy) ) / 2
lambda2 = ( Ixx + Iyy - sqrt( (Ixx-Iyy)^2 + 4.0*Ixy*Ixy) ) / 2
To get the line segment direction we want to get the angle the
eigenvector assotiated to the smaller eigenvalue. We have to solve
a,b in:
a.Ixx + b.Ixy = a.lambda2
a.Ixy + b.Iyy = b.lambda2
We want the angle theta = atan(b/a). It can be computed with
any of the two equations:
theta = atan( (lambda2-Ixx) / Ixy )
or
theta = atan( Ixy / (lambda2-Iyy) )
When |Ixx| > |Iyy| we use the first, otherwise the second (just to
get better numeric precision).
*/
static double get_theta( struct point *reg, int reg_size, double x, double y,
image_double modgrad, double reg_angle, double prec )
{
double lambda, theta, weight;
double Ixx = 0.0;
double Iyy = 0.0;
double Ixy = 0.0;
int i;
/* check parameters */
if ( reg == NULL ) error("get_theta: invalid region.");
if ( reg_size <= 1 ) error("get_theta: region size <= 1.");
if ( modgrad == NULL || modgrad->data == NULL )
error("get_theta: invalid 'modgrad'.");
if ( prec < 0.0 ) error("get_theta: 'prec' must be positive.");
/* compute inertia matrix */
for (i = 0; i < reg_size; i++)
{
weight = modgrad->data[ reg[i].x + reg[i].y * modgrad->xsize ];
Ixx += ( (double) reg[i].y - y ) * ( (double) reg[i].y - y ) * weight;
Iyy += ( (double) reg[i].x - x ) * ( (double) reg[i].x - x ) * weight;
Ixy -= ( (double) reg[i].x - x ) * ( (double) reg[i].y - y ) * weight;
}
if ( double_equal(Ixx, 0.0) && double_equal(Iyy, 0.0) && double_equal(Ixy, 0.0) )
error("get_theta: null inertia matrix.");
/* compute smallest eigenvalue */
lambda = 0.5 * ( Ixx + Iyy - sqrt( (Ixx - Iyy) * (Ixx - Iyy) + 4.0 * Ixy * Ixy ) );
/* compute angle */
theta = fabs(Ixx) > fabs(Iyy) ? atan2(lambda - Ixx, Ixy) : atan2(Ixy, lambda - Iyy);
/* The previous procedure don't cares about orientation,
so it could be wrong by 180 degrees. Here is corrected if necessary. */
if ( angle_diff(theta, reg_angle) > prec ) theta += M_PI;
return theta;
}
/*----------------------------------------------------------------------------*/
/** Computes a rectangle that covers a region of points.
*/
static void region2rect( struct point *reg, int reg_size,
image_double modgrad, double reg_angle,
double prec, double p, struct rect *rec )
{
double x, y, dx, dy, l, w, theta, weight, sum, l_min, l_max, w_min, w_max;
int i;
/* check parameters */
if ( reg == NULL ) error("region2rect: invalid region.");
if ( reg_size <= 1 ) error("region2rect: region size <= 1.");
if ( modgrad == NULL || modgrad->data == NULL )
error("region2rect: invalid image 'modgrad'.");
if ( rec == NULL ) error("region2rect: invalid 'rec'.");
/* center of the region:
It is computed as the weighted sum of the coordinates
of all the pixels in the region. The norm of the gradient
is used as the weight of a pixel. The sum is as follows:
cx = \sum_i G(i).x_i
cy = \sum_i G(i).y_i
where G(i) is the norm of the gradient of pixel i
and x_i,y_i are its coordinates.
*/
x = y = sum = 0.0;
for (i = 0; i < reg_size; i++)
{
weight = modgrad->data[ reg[i].x + reg[i].y * modgrad->xsize ];
x += (double) reg[i].x * weight;
y += (double) reg[i].y * weight;
sum += weight;
}
if ( sum <= 0.0 ) error("region2rect: weights sum equal to zero.");
x /= sum;
y /= sum;
/* theta */
theta = get_theta(reg, reg_size, x, y, modgrad, reg_angle, prec);
/* length and width:
'l' and 'w' are computed as the distance from the center of the
region to pixel i, projected along the rectangle axis (dx,dy) and
to the orthogonal axis (-dy,dx), respectively.
The length of the rectangle goes from l_min to l_max, where l_min
and l_max are the minimum and maximum values of l in the region.
Analogously, the width is selected from w_min to w_max, where
w_min and w_max are the minimum and maximum of w for the pixels
in the region.
*/
dx = cos(theta);
dy = sin(theta);
l_min = l_max = w_min = w_max = 0.0;
for (i = 0; i < reg_size; i++)
{
l = ( (double) reg[i].x - x) * dx + ( (double) reg[i].y - y) * dy;
w = -( (double) reg[i].x - x) * dy + ( (double) reg[i].y - y) * dx;
if ( l > l_max ) l_max = l;
if ( l < l_min ) l_min = l;
if ( w > w_max ) w_max = w;
if ( w < w_min ) w_min = w;
}
/* store values */
rec->x1 = x + l_min * dx;
rec->y1 = y + l_min * dy;
rec->x2 = x + l_max * dx;
rec->y2 = y + l_max * dy;
rec->width = w_max - w_min;
rec->x = x;
rec->y = y;
rec->theta = theta;
rec->dx = dx;
rec->dy = dy;
rec->prec = prec;
rec->p = p;
/* we impose a minimal width of one pixel
A sharp horizontal or vertical step would produce a perfectly
horizontal or vertical region. The width computed would be
zero. But that corresponds to a one pixels width transition in
the image.
*/
if ( rec->width < 1.0 ) rec->width = 1.0;
}
/*----------------------------------------------------------------------------*/
/** Build a region of pixels that share the same angle, up to a
tolerance 'prec', starting at point (x,y).
*/
static void region_grow( int x, int y, image_double angles, struct point *reg,
int *reg_size, double *reg_angle, image_char used,
double prec )
{
double sumdx, sumdy;
int xx, yy, i;
/* check parameters */
if ( x < 0 || y < 0 || x >= (int) angles->xsize || y >= (int) angles->ysize )
error("region_grow: (x,y) out of the image.");
if ( angles == NULL || angles->data == NULL )
error("region_grow: invalid image 'angles'.");
if ( reg == NULL ) error("region_grow: invalid 'reg'.");
if ( reg_size == NULL ) error("region_grow: invalid pointer 'reg_size'.");
if ( reg_angle == NULL ) error("region_grow: invalid pointer 'reg_angle'.");
if ( used == NULL || used->data == NULL )
error("region_grow: invalid image 'used'.");
/* first point of the region */
*reg_size = 1;
reg[0].x = x;
reg[0].y = y;
*reg_angle = angles->data[x + y * angles->xsize]; /* region's angle */
sumdx = cos(*reg_angle);
sumdy = sin(*reg_angle);
used->data[x + y * used->xsize] = USED;
/* try neighbors as new region points */
for (i = 0; i < *reg_size; i++)
for (xx = reg[i].x - 1; xx <= reg[i].x + 1; xx++)
for (yy = reg[i].y - 1; yy <= reg[i].y + 1; yy++)
if ( xx >= 0 && yy >= 0 && xx < (int)used->xsize && yy < (int)used->ysize &&
used->data[xx + yy * used->xsize] != USED &&
isaligned(xx, yy, angles, *reg_angle, prec) )
{
/* add point */
used->data[xx + yy * used->xsize] = USED;
reg[*reg_size].x = xx;
reg[*reg_size].y = yy;
++(*reg_size);
/* update region's angle */
sumdx += cos( angles->data[xx + yy * angles->xsize] );
sumdy += sin( angles->data[xx + yy * angles->xsize] );
*reg_angle = atan2(sumdy, sumdx);
}
}
/*----------------------------------------------------------------------------*/
/** Try some rectangles variations to improve NFA value. Only if the
rectangle is not meaningful (i.e., log_nfa <= eps).
*/
static double rect_improve( struct rect *rec, image_double angles,
double logNT, double eps )
{
struct rect r;
double log_nfa, log_nfa_new;
double delta = 0.5;
double delta_2 = delta / 2.0;
int n;
log_nfa = rect_nfa(rec, angles, logNT);
if ( log_nfa > eps ) return log_nfa;
/* try finer precisions */
rect_copy(rec, &r);
for (n = 0; n < 5; n++)
{
r.p /= 2.0;
r.prec = r.p * M_PI;
log_nfa_new = rect_nfa(&r, angles, logNT);
if ( log_nfa_new > log_nfa )
{
log_nfa = log_nfa_new;
rect_copy(&r, rec);
}
}
if ( log_nfa > eps ) return log_nfa;
/* try to reduce width */
rect_copy(rec, &r);
for (n = 0; n < 5; n++)
{
if ( (r.width - delta) >= 0.5 )
{
r.width -= delta;
log_nfa_new = rect_nfa(&r, angles, logNT);
if ( log_nfa_new > log_nfa )
{
rect_copy(&r, rec);
log_nfa = log_nfa_new;
}
}
}
if ( log_nfa > eps ) return log_nfa;
/* try to reduce one side of the rectangle */
rect_copy(rec, &r);
for (n = 0; n < 5; n++)
{
if ( (r.width - delta) >= 0.5 )
{
r.x1 += -r.dy * delta_2;
r.y1 += r.dx * delta_2;
r.x2 += -r.dy * delta_2;
r.y2 += r.dx * delta_2;
r.width -= delta;
log_nfa_new = rect_nfa(&r, angles, logNT);
if ( log_nfa_new > log_nfa )
{
rect_copy(&r, rec);
log_nfa = log_nfa_new;
}
}
}
if ( log_nfa > eps ) return log_nfa;
/* try to reduce the other side of the rectangle */
rect_copy(rec, &r);
for (n = 0; n < 5; n++)
{
if ( (r.width - delta) >= 0.5 )
{
r.x1 -= -r.dy * delta_2;
r.y1 -= r.dx * delta_2;
r.x2 -= -r.dy * delta_2;
r.y2 -= r.dx * delta_2;
r.width -= delta;
log_nfa_new = rect_nfa(&r, angles, logNT);
if ( log_nfa_new > log_nfa )
{
rect_copy(&r, rec);
log_nfa = log_nfa_new;
}
}
}
if ( log_nfa > eps ) return log_nfa;
/* try even finer precisions */
rect_copy(rec, &r);
for (n = 0; n < 5; n++)
{
r.p /= 2.0;
r.prec = r.p * M_PI;
log_nfa_new = rect_nfa(&r, angles, logNT);
if ( log_nfa_new > log_nfa )
{
log_nfa = log_nfa_new;
rect_copy(&r, rec);
}
}
return log_nfa;
}
/*----------------------------------------------------------------------------*/
/** Reduce the region size, by elimination the points far from the
starting point, until that leads to rectangle with the right
density of region points or to discard the region if too small.
*/
static int reduce_region_radius( struct point *reg, int *reg_size,
image_double modgrad, double reg_angle,
double prec, double p, struct rect *rec,
image_char used, image_double angles,
double density_th )
{
double density, rad1, rad2, rad, xc, yc;
int i;
/* check parameters */
if ( reg == NULL ) error("reduce_region_radius: invalid pointer 'reg'.");
if ( reg_size == NULL )
error("reduce_region_radius: invalid pointer 'reg_size'.");
if ( prec < 0.0 ) error("reduce_region_radius: 'prec' must be positive.");
if ( rec == NULL ) error("reduce_region_radius: invalid pointer 'rec'.");
if ( used == NULL || used->data == NULL )
error("reduce_region_radius: invalid image 'used'.");
if ( angles == NULL || angles->data == NULL )
error("reduce_region_radius: invalid image 'angles'.");
/* compute region points density */
density = (double) * reg_size /
( dist(rec->x1, rec->y1, rec->x2, rec->y2) * rec->width );
/* if the density criterion is satisfied there is nothing to do */
if ( density >= density_th ) return TRUE;
/* compute region's radius */
xc = (double) reg[0].x;
yc = (double) reg[0].y;
rad1 = dist( xc, yc, rec->x1, rec->y1 );
rad2 = dist( xc, yc, rec->x2, rec->y2 );
rad = rad1 > rad2 ? rad1 : rad2;
/* while the density criterion is not satisfied, remove farther pixels */
while ( density < density_th )
{
rad *= 0.75; /* reduce region's radius to 75% of its value */
/* remove points from the region and update 'used' map */
for (i = 0; i < *reg_size; i++)
if ( dist( xc, yc, (double) reg[i].x, (double) reg[i].y ) > rad )
{
/* point not kept, mark it as NOTUSED */
used->data[ reg[i].x + reg[i].y * used->xsize ] = NOTUSED;
/* remove point from the region */
reg[i].x = reg[*reg_size - 1].x; /* if i==*reg_size-1 copy itself */
reg[i].y = reg[*reg_size - 1].y;
--(*reg_size);
--i; /* to avoid skipping one point */
}
/* reject if the region is too small.
2 is the minimal region size for 'region2rect' to work. */
if ( *reg_size < 2 ) return FALSE;
/* re-compute rectangle */
region2rect(reg, *reg_size, modgrad, reg_angle, prec, p, rec);
/* re-compute region points density */
density = (double) * reg_size /
( dist(rec->x1, rec->y1, rec->x2, rec->y2) * rec->width );
}
/* if this point is reached, the density criterion is satisfied */
return TRUE;
}
/*----------------------------------------------------------------------------*/
/** Refine a rectangle.
For that, an estimation of the angle tolerance is performed by the
standard deviation of the angle at points near the region's
starting point. Then, a new region is grown starting from the same
point, but using the estimated angle tolerance. If this fails to
produce a rectangle with the right density of region points,
'reduce_region_radius' is called to try to satisfy this condition.
*/
static int refine( struct point *reg, int *reg_size, image_double modgrad,
double reg_angle, double prec, double p, struct rect *rec,
image_char used, image_double angles, double density_th )
{
double angle, ang_d, mean_angle, tau, density, xc, yc, ang_c, sum, s_sum;
int i, n;
/* check parameters */
if ( reg == NULL ) error("refine: invalid pointer 'reg'.");
if ( reg_size == NULL ) error("refine: invalid pointer 'reg_size'.");
if ( prec < 0.0 ) error("refine: 'prec' must be positive.");
if ( rec == NULL ) error("refine: invalid pointer 'rec'.");
if ( used == NULL || used->data == NULL )
error("refine: invalid image 'used'.");
if ( angles == NULL || angles->data == NULL )
error("refine: invalid image 'angles'.");
/* compute region points density */
density = (double) * reg_size /
( dist(rec->x1, rec->y1, rec->x2, rec->y2) * rec->width );
/* if the density criterion is satisfied there is nothing to do */
if ( density >= density_th ) return TRUE;
/*------ First try: reduce angle tolerance ------*/
/* compute the new mean angle and tolerance */
xc = (double) reg[0].x;
yc = (double) reg[0].y;
ang_c = angles->data[ reg[0].x + reg[0].y * angles->xsize ];
sum = s_sum = 0.0;
n = 0;
for (i = 0; i < *reg_size; i++)
{
used->data[ reg[i].x + reg[i].y * used->xsize ] = NOTUSED;
if ( dist( xc, yc, (double) reg[i].x, (double) reg[i].y ) < rec->width )
{
angle = angles->data[ reg[i].x + reg[i].y * angles->xsize ];
ang_d = angle_diff_signed(angle, ang_c);
sum += ang_d;
s_sum += ang_d * ang_d;
++n;
}
}
mean_angle = sum / (double) n;
tau = 2.0 * sqrt( (s_sum - 2.0 * mean_angle * sum) / (double) n
+ mean_angle * mean_angle ); /* 2 * standard deviation */
/* find a new region from the same starting point and new angle tolerance */
region_grow(reg[0].x, reg[0].y, angles, reg, reg_size, ®_angle, used, tau);
/* if the region is too small, reject */
if ( *reg_size < 2 ) return FALSE;
/* re-compute rectangle */
region2rect(reg, *reg_size, modgrad, reg_angle, prec, p, rec);
/* re-compute region points density */
density = (double) * reg_size /
( dist(rec->x1, rec->y1, rec->x2, rec->y2) * rec->width );
/*------ Second try: reduce region radius ------*/
if ( density < density_th )
return reduce_region_radius( reg, reg_size, modgrad, reg_angle, prec, p,
rec, used, angles, density_th );
/* if this point is reached, the density criterion is satisfied */
return TRUE;
}
/*----------------------------------------------------------------------------*/
/*-------------------------- Line Segment Detector ---------------------------*/
/*----------------------------------------------------------------------------*/
/*----------------------------------------------------------------------------*/
/** LSD full interface.
*/
ntuple_list LineSegmentDetection( image_double image, double scale,
double sigma_scale, double quant,
double ang_th, double eps, double density_th,
int n_bins, double max_grad,
image_int *region )
{
ntuple_list out = new_ntuple_list(5);
image_double scaled_image, angles, modgrad;
image_char used;
struct coorlist *list_p;
void *mem_p;
struct rect rec;
struct point *reg;
int reg_size, min_reg_size, i;
unsigned int xsize, ysize;
double rho, reg_angle, prec, p, log_nfa, logNT;
int ls_count = 0; /* line segments are numbered 1,2,3,... */
/* check parameters */
if ( image == NULL || image->data == NULL || image->xsize == 0 || image->ysize == 0 )
error("invalid image input.");
if ( scale <= 0.0 ) error("'scale' value must be positive.");
if ( sigma_scale <= 0.0 ) error("'sigma_scale' value must be positive.");
if ( quant < 0.0 ) error("'quant' value must be positive.");
if ( ang_th <= 0.0 || ang_th >= 180.0 )
error("'ang_th' value must be in the range (0,180).");
if ( density_th < 0.0 || density_th > 1.0 )
error("'density_th' value must be in the range [0,1].");
if ( n_bins <= 0 ) error("'n_bins' value must be positive.");
if ( max_grad <= 0.0 ) error("'max_grad' value must be positive.");
/* angle tolerance */
prec = M_PI * ang_th / 180.0;
p = ang_th / 180.0;
rho = quant / sin(prec); /* gradient magnitude threshold */
/* scale image (if necessary) and compute angle at each pixel */
if ( scale != 1.0 )
{
scaled_image = gaussian_sampler( image, scale, sigma_scale );
angles = ll_angle( scaled_image, rho, &list_p, &mem_p,
&modgrad, (unsigned int) n_bins, max_grad );
free_image_double(scaled_image);
}
else
angles = ll_angle( image, rho, &list_p, &mem_p, &modgrad,
(unsigned int) n_bins, max_grad );
xsize = angles->xsize;
ysize = angles->ysize;
logNT = 5.0 * ( log10( (double) xsize ) + log10( (double) ysize ) ) / 2.0;
min_reg_size = (int) (-logNT / log10(p)); /* minimal number of points in region
that can give a meaningful event */
/* initialize some structures */
if ( region != NULL ) /* image to output pixel region number, if asked */
*region = new_image_int_ini(angles->xsize, angles->ysize, 0);
used = new_image_char_ini(xsize, ysize, NOTUSED);
reg = (struct point *) calloc( (size_t) (xsize * ysize), sizeof(struct point) );
if ( reg == NULL ) error("not enough memory!");
/* search for line segments */
for (; list_p != NULL; list_p = list_p->next )
if ( used->data[ list_p->x + list_p->y * used->xsize ] == NOTUSED &&
angles->data[ list_p->x + list_p->y * angles->xsize ] != NOTDEF )
/* there is no risk of double comparison problems here
because we are only interested in the exact NOTDEF value */
{
/* find the region of connected point and ~equal angle */
region_grow( list_p->x, list_p->y, angles, reg, ®_size,
®_angle, used, prec );
/* reject small regions */
if ( reg_size < min_reg_size ) continue;
/* construct rectangular approximation for the region */
region2rect(reg, reg_size, modgrad, reg_angle, prec, p, &rec);
/* Check if the rectangle exceeds the minimal density of
region points. If not, try to improve the region.
The rectangle will be rejected if the final one does
not fulfill the minimal density condition.
This is an addition to the original LSD algorithm published in
"LSD: A Fast Line Segment Detector with a False Detection Control"
by R. Grompone von Gioi, J. Jakubowicz, J.M. Morel, and G. Randall.
The original algorithm is obtained with density_th = 0.0.
*/
if ( !refine( reg, ®_size, modgrad, reg_angle,
prec, p, &rec, used, angles, density_th ) ) continue;
/* compute NFA value */
log_nfa = rect_improve(&rec, angles, logNT, eps);
if ( log_nfa <= eps ) continue;
/* A New Line Segment was found! */
++ls_count; /* increase line segment counter */
/*
The gradient was computed with a 2x2 mask, its value corresponds to
points with an offset of (0.5,0.5), that should be added to output.
The coordinates origin is at the center of pixel (0,0).
*/
rec.x1 += 0.5; rec.y1 += 0.5;
rec.x2 += 0.5; rec.y2 += 0.5;
/* scale the result values if a subsampling was performed */
if ( scale != 1.0 )
{
rec.x1 /= scale; rec.y1 /= scale;
rec.x2 /= scale; rec.y2 /= scale;
rec.width /= scale;
}
/* add line segment found to output */
add_5tuple(out, rec.x1, rec.y1, rec.x2, rec.y2, rec.width);
/* add region number to 'region' image if needed */
if ( region != NULL )
for (i = 0; i < reg_size; i++)
(*region)->data[reg[i].x + reg[i].y * (*region)->xsize] = ls_count;
}
/* free memory */
free_image_double(angles);
free_image_double(modgrad);
free_image_char(used);
free( (void *) reg );
free( (void *) mem_p );
return out;
}
/*----------------------------------------------------------------------------*/
/** LSD Simple Interface with Scale.
*/
ntuple_list lsd_scale(image_double image, double scale)
{
/* LSD parameters */
double sigma_scale = 0.6; /* Sigma for Gaussian filter is computed as
sigma = sigma_scale/scale. */
double quant = 2.0; /* Bound to the quantization error on the
gradient norm. */
double ang_th = 22.5; /* Gradient angle tolerance in degrees. */
double eps = 0.0; /* Detection threshold, -log10(NFA). */
double density_th = 0.7; /* Minimal density of region points in rectangle. */
int n_bins = 1024; /* Number of bins in pseudo-ordering of gradient
modulus. */
double max_grad = 255.0; /* Gradient modulus in the highest bin. The
default value corresponds to the highest
gradient modulus on images with gray
levels in [0,255]. */
return LineSegmentDetection( image, scale, sigma_scale, quant, ang_th, eps,
density_th, n_bins, max_grad, NULL );
}
/*----------------------------------------------------------------------------*/
/** LSD Simple Interface.
*/
ntuple_list lsd(image_double image)
{
/* LSD parameters */
double scale = 0.8; /* Scale the image by Gaussian filter to 'scale'. */
return lsd_scale(image, scale);
}
/*----------------------------------------------------------------------------*/ main
#include
#include
#include
#include
#include
#include "lsd.h"
using namespace cv;
using namespace std;
void HoughLinesDetect(const cv::Mat& src);
void GetRotateLSDAngle(const cv::Mat& srcImg);
void GetRotateLSDAngle(const cv::Mat& srcImg)
{
double start = double(getTickCount());
double angle = 0.0;
int lineDisThreshold = 153; //排除小于此长度的短线段 103
double angleRange = 0.5; //以此角度为区间对线段进行分区间统计频率
if (srcImg.empty())
{
return ;
}
Mat src_gray, src_corlor;
if (srcImg.channels() == 3)
{
cv::cvtColor(srcImg, src_gray, CV_RGB2GRAY);
src_corlor = srcImg.clone();
}
else
{
src_gray = srcImg.clone();
cvtColor(srcImg, src_corlor, CV_GRAY2BGR);
}
src_gray.convertTo(src_gray, CV_64FC1);
int cols = src_gray.cols;
int rows = src_gray.rows;
image_double image = new_image_double(cols, rows);
Mat imageline = cv::Mat::zeros(rows, cols, CV_8UC1);
double *data = image->data;
image->data = src_gray.ptr(0);
ntuple_list ntl = lsd(image);
double duration_ms = (double(getTickCount()) - start) * 1000 / getTickFrequency();
cout << "LsdLine took " << duration_ms << " ms." << endl;
cout << "LsdLine size = " << ntl->size << endl;
Point pt1, pt2;
for (int j = 0; j != ntl->size; ++j)
{
pt1.x = int(ntl->values[0 + j * ntl->dim]);
pt1.y = int(ntl->values[1 + j * ntl->dim]);
pt2.x = int(ntl->values[2 + j * ntl->dim]);
pt2.y = int(ntl->values[3 + j * ntl->dim]);
//int linewidth = int(ntl->values[4 + j * ntl->dim]);
// line(src_corlor, pt1, pt2, Scalar(0, 255, 0), 1, 4);
line(imageline, pt1, pt2, cv::Scalar(255), 1, CV_AA);
}
free_ntuple_list(ntl);
free(data);
//namedWindow("LsdLine", 0);
//imshow("LsdLine", src_corlor);
namedWindow("LsdLine", 0);
imshow("LsdLine", imageline);
}
void HoughLinesDetect(const cv::Mat& src)
{
double start = double(getTickCount());
if (src.empty())
{
return;
}
Mat src_gray, src_corlor, CannyImg;
if (src.channels() == 3)
{
cv::cvtColor(src, src_gray, CV_RGB2GRAY);
src_corlor = src.clone();
}
else
{
src_gray = src.clone();
cvtColor(src, src_corlor, CV_GRAY2BGR);
}
int cols = src_gray.cols;
int rows = src_gray.rows;
// threshold(src_gray, CannyImg, 150, 255, CV_THRESH_BINARY);
Canny(src_gray, CannyImg, 40, 250, 3);
vector Lines;
HoughLinesP(CannyImg, Lines, 1, CV_PI / 180, 10, 7, 2);
Mat imageline = cv::Mat::zeros(rows, cols, CV_8UC1);
double duration_ms = (double(getTickCount()) - start) * 1000 / getTickFrequency();
cout << "HoughLine took " << duration_ms << " ms." << endl;
cout << "HoughLine size = " << Lines.size()<< endl;
if (Lines.size() != 0)
{
for (size_t i = 0; i < Lines.size(); i++)
{
line(imageline, Point(Lines[i][0], Lines[i][1]), Point(Lines[i][2], Lines[i][3]), cv::Scalar(255), 1, CV_AA);
// line(src_corlor, Point(Lines[i][0], Lines[i][1]), Point(Lines[i][2], Lines[i][3]), Scalar(0, 0, 255), 1, 4);
}
}
//namedWindow("HoughLine", 0);
//imshow("HoughLine", src_corlor);
namedWindow("HoughLine", 0);
imshow("HoughLine", imageline);
}
int main(int argc, char **argv)
{
char *srcImage = "line.png";
Mat srcImg = imread(srcImage,1);
namedWindow("srcImg", 0);
imshow("srcImg", srcImg);
HoughLinesDetect(srcImg);
GetRotateLSDAngle(srcImg);
waitKey(0);
system("pause");
return 0;
}
效果