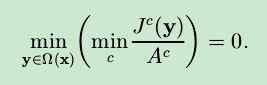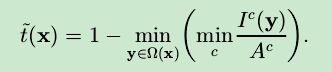图像去雾算法（二）基于暗通道先验算法学习笔记

在http://write.blog.csdn.net/postedit/78301999中介绍了图像去雾的相关研究方法，发现目前为止在图像去雾方面，何凯明博士基于暗通道先验的算法具有很好的效果，关于该方法的介绍也很多，本篇作下学习笔记和个人理解：

Retinex背景知识

（1）

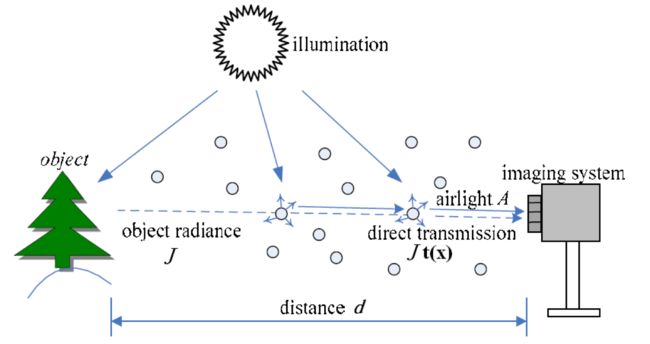
图像去雾过程就是根据 I(x) 求解 J(x) 的过程。从上面的公式可以看出，基于物理模型的去雾算法本质是根据已知的有雾图像 I(x) 求出透射率 t(x) 和全局大气光成分A （A>0），进而得到复原图像J(X)（场景光成分）。在参考【2】里有关于该模型的详细解释，其中J(x)t(x)是直接衰减（direct attenuation），A(1-t(x)) 是空气光（airlight）。当大气是同质（说的应该是均匀分布吧）时，传输率t表示为：

                                                                                                                                           （2）

其中，β是大气的散射系数，d是场景光线的景深。

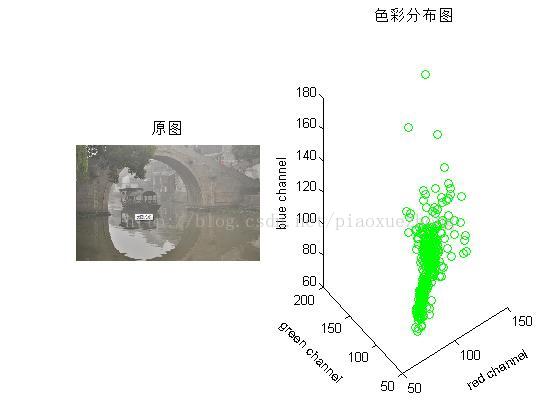
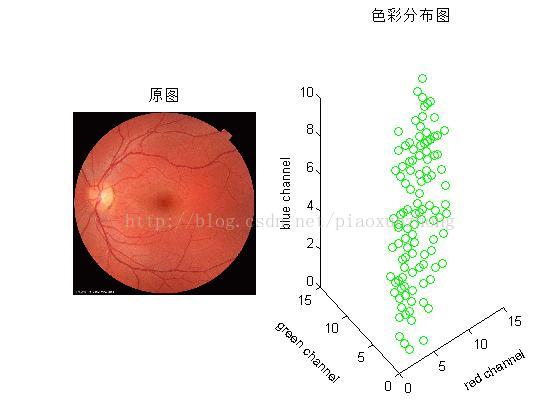
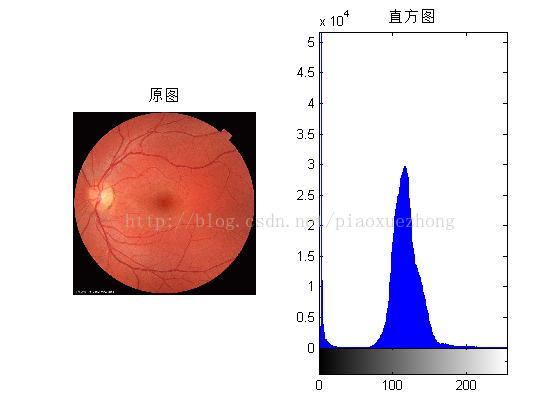
有雾图像特征：

上面几幅图是图像的彩色分布图和直方图，一般的，有雾图像的RGB色彩分布图比较集中，直方图范围也窄，相对集中；清晰图像的RGB色彩分布图比较广泛，直方图分布均匀，色彩感较强。

基于暗通道先验去雾算法原理：

下面是原作者的一些感言：

简单有效的图像去雾技术

这篇论文研究的问题是图像的去雾技术，它可以还原图像的颜色和能见度，同时也能利用雾的浓度来估计物体的距离，这些在计算机视觉上都有重要应用（例如三维重建，物体识别）。但是之前人们还没找到简单有效的方法来达到这个目的。在这篇论文里，我们找到了一个非常简单的，甚至说令人惊讶统计规律，并提出了有效的去雾方法。
与之前的方法不同，我们把注意力放到了无雾图像的统计特征上。我们发现，在无雾图像中，每一个局部区域都很有可能会有阴影，或者是纯颜色的东西，又或者是黑色的东西。因此，每一个局部区域都很有可能有至少一个颜色通道会有很低的值。我们把这个统计规律叫做Dark Channel Prior。直观来说，Dark Channel Prior认为每一个局部区域都总有一些很暗的东西。这个规律很简单，但在我们研究的去雾问题上却是本质的基本规律。
由于雾总是灰白色的，因此一旦图像受到雾的影响，那么这些本来应该很暗的东西就会变得灰白。不仅如此，根据物理上雾的形成公式，我们还能根据这些东西的灰白程度来判断雾的浓度。因此，我们提出的Dark Channel Prior能很有效地去除雾的影响，同时利用物的浓度来估算物体的距离。

大道之行在于简

我们这篇文章的三个审稿人都给出了最高的评分。他们认为我们的方法简单而有效。其中一位评委说，Dark Channel Prior的想法听起来很不可思议，但我们却证明了其真实性。另一位评委认为很少有文章能够用如此简单的方法使实验结果获得如此大的提升。还有一位评委甚至亲自实现了我们的方法并确认其可行。孙剑说阅读这样的评审结果是一件让人快乐的事情。而汤老师认为，这篇文章的成功在于三个方面。第一，方法非常简单；第二，对于一个很困难的问题，给出了很好的结果；第三，发现了一个基本的自然规律并且应用在实际的问题中。在迈阿密的演讲结束后，观众也给予了很高的评价。他们跟我说，这是这次CVPR上最有趣的一个演讲。
一位与会的研究员说，最好的idea，往往就是那些看起来很简单，但说出来大家都会觉得怎么没有人想到过的idea。而我们的idea正好就符合了这一点。我们论文摘要的第一句话是这么说的，“我们提出了一个简单而有效的方法”。或许，这就是对我们这次工作最好的概括——简单的，就是美的。

下面正式展开基于暗通道去雾算法的原理部分：

从上面的式（1）可以看出，A, I, J 三个向量是共面的，并且末端点共线，并可以推出t的表达式（3）：

暗通道先验：

关于暗通道先验的概念，在作者的感言部分有很清楚的解释，就不再说了。其求法如下：

                    (4)

Ω(x)表示以x为中心的局部块，c为三个通道，Jc表示图像J的彩色通道图像。即先求出rgb通道中像素的最小值，然后将其存进和原始图像尺寸相同的灰度图中，再对该灰度图进行最小值滤波。

若 J 是无雾霾图像，除了天空区域，式（4）的值趋近与0，另外作者给出了暗通道存在的几个原因：
（1）阴影。比如：在城市景观中的车辆、建筑物和窗户内部的阴影；在自然风景中的树叶、树木和岩石的阴影。
（2）彩色物体或表面。比如：低反射率彩色通道的物体（如绿草、树，红花或叶子，蓝色的水面）容易在暗通道产生亮度低的值。
（3）暗的对象或表面。比如：暗的树和石头。

由于户外的图像通常都有阴影并且色彩斑斓，所以这些图像的暗通道确实很暗。

估计传输率 t：

假设大气光 A 已知，式（1）可以推出：

    ，                                （5）

进一步假设局部块Ω(x)是连续的，块的传输率为 t~，式（5）对每个通道去最小值运算，

t~(x)

  ，   （6）

由于式（4）趋近于0，A>0，所以有：

，                                                  （7）

把式（7）带入（6），得到：

,                                      （8）

由于天空在无限远处且传输率趋于0，所以式（8）此时也是可以满足的。同时考虑到大气透视（aerial perspective）现象的存在，如果完全移除雾霾，图像看起来会不自然并且可能丢失深度信息，所以需要对远处的对象保留少量的雾霾，于是在式（8）中引入了恒参w,一般取值为0.95，式（8）变为：

                                   （9）

基于暗通道先验去雾算法的缺陷：

暗原色先验是一种统计的结果，是对大量户外无雾照片的统计结果，如果目标场景内存在和大气光类似，比如雪地、白色背景墙、大海等，那么由于前提条件就不成立，此时将无法获得满意的效果，但是对于一般的风景照片该算法处理效果会不错。

基于暗通道先验去雾算法实现：

式（4）求暗通道先验时，进行两部取最小值操作，该算法的快速实现可以参见【3】 ，这个算法的时间复杂度是O(1)。后来，作者有针对算法效率进行改进，使用了引导滤波算法，

具体代码请参见参考附录里的博客。我这里只附录下Richal_zhang的matlab实现，她的是按照论文里最基本的实现：

%=========================================================%  
%调用规则：（有雾时调用，否则不调用）  
%实际操作时,according to experiments：  
%percent=under_50/total  
%percent<0.1%,取w=0.6  
%percent>0.1%&&percent<1%,取w=0.45  
%percenet>1%&&percent<2%,取w=0.3  
%else not use haze-free-adjust  
%有雾：绘制出的直方图<50的部分<1%  
%最后控制台还会输出原图中under_50像素点所占比例  
%=========================================================%  
close all  
clear all  
clc  
blockSize=15;               %每个block为15个像素  
w0=0.6;                      
t0=0.1;  
% A=200;  
I=imread('D:\fcq_proMatlab\test_image\fog\5.jpg');  
h = figure;  
%set(gcf,'outerposition',get(0,'screensize'));%获得SystemScreenSize 传递给当前图像句柄gcf的outerposition属性  
subplot(321)%表示3（行数）*2（列数）的图像，1代表所画图形的序号  
imshow(I);  
title('Original Image');  


subplot(323);  
grayI=rgb2gray(I);  
imshow(grayI,[]);  
title('原图像灰度图')  

subplot(324);  
imhist(grayI,64);  

%统计<50的像素所占的比例  
%%%%%%%%%%%%%%%%%%%%%%  
[COUNT x]=imhist(grayI);  
under_50=0;  
for i=0:50  
    under_50=under_50+COUNT(x==i);  
end  
under_50  
total=size(I,1)*size(I,2)*size(I,3);  
percent=under_50/total;
%%%%%%%%%%%%%%%%%%%%%%  

if(percent>0.02)  
    error('This image need not Haze-Free-Proprocessing.');  
else if(percent<0.001)  
        w=0.6;  
    else if (percent>0.01)  
            w=0.3;  
        else  
            w=0.45;  
        end  
    end  
end  

[h,w,s]=size(I);  
min_I=zeros(h,w);  

for i=1:h                   
    for j=1:w  
        dark_I(i,j)=min(I(i,j,:));%取每个点的像素为RGB分量中最低的那个通道的值  
    end  
end  

Max_dark_channel=double(max(max(dark_I)));  
dark_channel=double(dark_I);  
t=1-w0*(dark_channel/Max_dark_channel);  

T=uint8(t*255);  

t=max(t,t0);  

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%  
I1=double(I);  
J(:,:,1) = uint8((I1(:,:,1) - (1-t)*Max_dark_channel)./t);  

J(:,:,2) = uint8((I1(:,:,2) - (1-t)*Max_dark_channel)./t);  

J(:,:,3) =uint8((I1(:,:,3) - (1-t)*Max_dark_channel)./t);  
subplot(322)  
imshow(J);  
title('Haze-Free Image:');  

subplot(325);  
grayJ=rgb2gray(J);  
imshow(grayJ,[]);  
title('去雾后灰度图')  

subplot(326);  
imhist(grayJ,64);  

参考：

• 《图像去雾的最新研究进展》[J]. 自动化学报
• 《Visibility in Bad Weather from a Single Image》[J].IEEE
• 《STREAMING MAXIMUM-MINIMUM FILTER USING NO MORE THAN THREE COMPARISONS PER ELEMENT》
• http://qianjiye.de/2015/09/haze-removal-kaiming#outline_0
  
• http://blog.csdn.net/u011691310/article/details/16827695
• http://blog.csdn.net/baimafujinji/article/details/27206237
• http://blog.csdn.net/baimafujinji/article/details/30060161
• http://www.cnblogs.com/Imageshop/p/3281703.html
• http://blog.csdn.net/s12244315/article/details/50292049