背包问题（greedy+dfs+dp）

背包问题（部分+01 greedy+dfs+dp）

部分背包问题

（背包重量符合要求=》背包价值max）
部分背包问题，指的是物品可以以任何大小放到背包中。
这个问题相较于0-1背包问题要更简单，包是可以在物体总质量>背包质量的情况下塞满的！所以单位重量价值越大越好！（用结构体去表示物体的质量、价值和单位价值）

使用贪心算法解决此问题：

#include 
#include 
#include 

using namespace std;
int w[5] = {3, 4, 6, 10, 7};     //重量
int v[5] = {15, 16, 18, 25, 14}; //价
//结构体
typedef struct
{
    int weight;
    int value;
    float vperw;
} good;
//比较
bool cmp(good a, good b)
{
    return a.vperw > b.vperw;
}
int main()
{
    int w[5] = {3, 4, 6, 10, 7};     //重量
    int v[5] = {15, 16, 18, 25, 14}; //价值
    int maxvalue = 0;
    int W;
    cin >> W; //输入限制的背包总质量
    vector<good> thing;
    good g;
    for (int i = 0; i < 5; i++)
    {
        g.value = v[i];
        g.weight = w[i];
        g.vperw = v[i] / w[i];
        thing.push_back(g);
    }
    sort(thing.begin(), thing.end(), cmp);
    for (int i = 0; i < 5; i++)
    {
        maxvalue += (W > thing[i].weight) ? thing[i].weight * thing[i].vperw : W * thing[i].vperw;
        cout << "装载物品价值：" << thing[i].value;
        if (W > thing[i].weight)
        {
            cout << "  装载物品质量：" << thing[i].weight;
        }
        else
        {
            cout << "  装载物品质量：" << W;
        }
        cout << endl;

        W -= thing[i].weight;
        if (W <= 0)
        {
            break;
        }
    }
    cout << "最大价值：" << maxvalue;
}

01背包问题

顾名思义就是物品只有两种状态，放或者不放。
举个老师课件上例子：

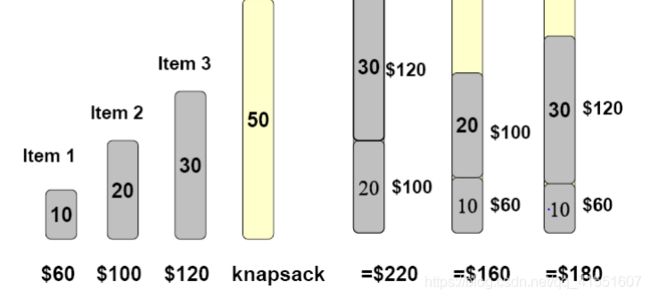
在这个例子可以看到背包的容量是50，三件物品的容量是10，20，30。倘若按照部分背包问题进行求解，可以得到将item1、item2放入背包中，因为它们的单位价值较高，但这时item3就放不进去了，所以贪心算法无法解决01背包问题，我们要对背包容量和物品容量及价值做一个综合的考量，每一个物品都有放和不放的两种状态，需要我们去尝试和试探。试探一次，容易想到回溯dfs，这是这类问题的一种解法，在这里给出dfs解法。

#include
using namespace std;
int n=0;
const int maxn = 100;
int w[maxn];//物品重量
int v[maxn];//物品价值
int C=0;//背包容量
int maxvalue=0;//当前最大价值


void dfs(int index,int sumw,int sumv){
    //dfs终止条件
    if(index==n){//n为物品个数
        if(sumw<=C&&sumv>=maxvalue){//<=C
            maxvalue = sumv;
        }
        return;
    }
    //选第i件物品
    dfs(index + 1, sumw + w[index], sumv + v[index]);
    //不选第i件物品
    dfs(index + 1, sumw, sumv);
}

int main()
{
    cout << "输入物品个数：";
    cin >> n;
    cout << "输入背包容量：";
    cin >> C;
    cout << "依此输入物品重量：";
    for (int i = 0; i < n;i++){
        cin >> w[i];
    }
    cout << "依此输入物品价值：";
    for (int i = 0; i < n;i++){
        cin >> v[i];
    }
    dfs(0, 0, 0);
    cout << "最大价值是" << maxvalue;

}

dfs有自己的书写格式

dfs(){
	if(终止条件） return;
	dfs()

下面考虑使用动态规划解决这个问题：
动态规划有两个前提条件：重叠子问题和最优子结构。
我们来观察01背包问题：
使用 dp[i-1][w] 表示前i-1个物品放入容量为w的背包的最大价值。
那么放入第i物品时，就有两种考虑情况：

• 放了！那么dp[i][w]=dp[i][w-w[i]]+v[i]
• 没放！那么dp[i][w]=dp[i-1][w]

这个时候最优出来做决定，选择max即可,再加上边界条件即可。

int main()
{
    int n, w;//物品数目，背包容量
    cout << "请输入物品数目:";
    cin >> n;
    cout<< "请输入背包容量:";
    cin >> w;
    int weight[n];
    int value[n];
    cout << "依次输入物品重量:";
    for (int i = 1; i <=n; i++)
    {
        cin >> weight[i];
    }
    cout << "依次输入物品价值:";
    for (int i = 1; i <= n; i++)
    {
        cin >> value[i];
    }
    //dp运算
    for (int i = 0; i <= n; i++)
    {

        for (int j = 0; j <= w; j++)
        {
             if(i==0||j==0){
                 dp[i][j] = 0;
             }
             if(j<weight[i]){
                 dp[i][j] = dp[i - 1][j];
             }
             else{
                 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
             }
        }
    }
    cout << "最大价值:" << dp[n][w];
}