递归和分治 机考复习

递归策略

1. 子问题必须与原始问题相同，且规模更小
2. 不能无限制地调用本身，必须有一个递归出口

汉诺塔

原始问题：

三根杆，64个圆盘，不允许大圆盘放到小圆盘上，从最左边的杆子移动到最右边
规律：n个圆盘=》2^n-1

#include 
using namespace std;
int count = 0; //起始次数为0
void hanoe(int num, int start, int mid, int end)
{ //圆盘数，开始杆，中间杆，结束杆
    if (num != 0)
    {
        hanoe(num - 1, start, end, mid); //移动上面num-1个
        //cout << start << "->" << end<
        count++;
        hanoe(num - 1, mid, end, start);
    }
}

int main()
{
    hanoe(5, 1, 2, 3);
    cout << count;
    return 0;
}

升级：

增加一个条件：不允许直接从最左（右）边移动到最右（左）边
输入：圆盘数目（多组数据）
输出：移动的最小次数

#include
using namespace std;
int count(int n){
    if(n==1){
        return 2;
    }else{
        return 3 * count(n - 1) + 2;
    }
}

int main(){
    int n;
    while(cin>>n){
        cout << count(n);
    }
    return 0;
}

杨辉三角形

题目描述
输入n值，使用递归函数，求杨辉三角形中各个位置上的值。
输入描述:
一个大于等于2的整型数n
输出描述:
题目可能有多组不同的测试数据，对于每组输入数据，
按题目的要求输出相应输入n的杨辉三角形。

自己在IDEA上写的代码是可以打印出正确结果的，但是实际上无法通过，整体逻辑比较混乱，不可取

#include
#include
using namespace std;
//生成前n-1行的杨辉三角形，最后一行根据前一行变
vector<vector<int>> yanghui(int n){
    vector<vector<int>> res;
    if(n==1){
        vector<int> tmp;
        tmp.push_back(1);
        res.push_back(tmp);
        return res;
    }
    res=yanghui(n-1);
    vector<int> end;
    end.push_back(1);
    //取出最后一个向量
    vector<int> tmp=res[n-2];
    for(int i=0;i<n-2;i++){
        end.push_back(tmp[i]+tmp[i+1]);
    }
    end.push_back(1);  
    res.push_back(end);
    return res;
}
void print(vector<int> tmp){
    for(int i=0;i<tmp.size();i++){
        cout<<tmp[i]<<" ";
    }
    cout<<endl;
}
int main(){
    vector<vector<int>> res;
    int n;
    cin >> n;
    res=yanghui(n);
    for(int i=0;i<n;i++){
        print(res[i]);
    }
    return 0;
}

还是没有把递归理解透彻，看了别人的代码，将子问题划分为一个一个值的求解。

#include
using namespace std;
int yanghui(int i,int j){//i，j出元素
    if(j==1){
        return 1;
    }
    if(i==j){
        return j;
    }
    return yanghui(i - 1, j - 1) + yanghui(i - 1, j);
}

int main(){
    int n;
    cin >> n;
    for (int i = 1; i <= n;i++){
        for (int j = 1; j <= i;j++){
            cout << yanghui(i, j) << " ";
        }
        cout << endl;
    }
}

全排列问题

题目描述
给定一个由不同的小写字母组成的字符串，输出这个字符串的所有全排列。 我们假设对于小写字母有’a’ < ‘b’ < … < ‘y’ < ‘z’，而且给定的字符串中的字母已经按照从小到大的顺序排列。
输入描述:
输入只有一行，是一个由不同的小写字母组成的字符串，已知字符串的长度在1到6之间。
输出描述:
输出这个字符串的所有排列方式，每行一个排列。要求字母序比较小的排列在前面。字母序如下定义：
已知S = s1s2…sk , T = t1t2…tk，则S < T 等价于，存在p (1 <= p <= k)，使得
s1 = t1, s2 = t2, …, sp - 1 = tp - 1, sp < tp成立。

每组样例输出结束后要再输出一个回车。

这属于难度较小的全排列问题，但是在做的过程中受到思维定式的影响，想着字符串中index的问题，实际上每一次取得字符只要前面没有被取过就好了。
而对于字母序处理，只要保证原始字符串是按照从小到大处理的就好。

//全排列
#include 
#include
#include 
#include
using namespace std;
void dfs(string s, vector<bool> &isvisit, string tmp)
{
    //结束条件
    if(tmp.size()==s.size()){
        cout << tmp << endl;
        tmp = "";
        return;
    }
    //选择列表
    for(int i=0;i<s.size();i++){
        if(isvisit[i]==true){
            continue;
        }
        //做选择
        tmp.push_back(s[i]);
        //cout << tmp << endl;
        isvisit[i]=true;
        dfs(s,isvisit,tmp);
        //撤销选择
        isvisit[i]=false;
        tmp.pop_back();
    }
}
void Fullarray(string s){
    string tmp;
    if(s.size()==0){
        return;
    }
    vector<bool> isvisit = {false};
    dfs(s,isvisit,tmp);
}

int main(){
    string s;
    while(cin>>s){
        sort(s.begin(),s.end());
        Fullarray(s);
        cout<<endl;
    }
}

分治

只要找到递推公式，都不困难。（自顶向下）
斐波那契数列
走楼梯（走一步，走两步）

二叉树

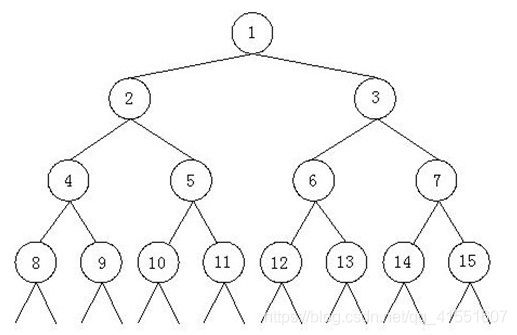
题目描述
如上所示，由正整数1，2，3……组成了一颗特殊二叉树。我们已知这个二叉树的最后一个结点是n。现在的问题是，结点m所在的子树中一共包括多少个结点。 比如，n = 12，m = 3那么上图中的结点13，14，15以及后面的结点都是不存在的，结点m所在子树中包括的结点有3，6，7，12，因此结点m的所在子树中共有4个结点。
输入描述:
输入数据包括多行，每行给出一组测试数据，包括两个整数m，n (1 <= m <= n <= 1000000000)。
输出描述:
对于每一组测试数据，输出一行，该行包含一个整数，给出结点m所在子树中包括的结点的数目。

要找到合适的底层子问题，在完成这道题时将底层子问题考虑成叶子节点，程序出现部分错误，因为并非平衡。
应该考虑成叶子节点下的空节点（m>n）的情况。

#include 
using namespace std;
int count(int m, int n)
{ //n为结点数目
    if (m>n)//递归结束
    {
        return 0;
    }
    return count(2 * m, n) + count(2 * m + 1, n)+1; //+1值加上当今的节点
}

int main()
{
    int m, n;
    while (cin >> m >> n)
    {
        if (m == 0 || n == 0)
        {
            break;
        }
        cout << count(m, n) << endl;
    }
}

二的幂次方

Every positive number can be presented by the exponential form.For example, 137 = 2^7 + 2^3 + 2^0。 Let’s present a^b by the form a(b).Then 137 is presented by 2(7)+2(3)+2(0). Since 7 = 2^2 + 2 + 2^0 and 3 = 2 + 2^0 , 137 is finally presented by 2(2(2)+2 +2(0))+2(2+2(0))+2(0). Given a positive number n,your task is to present n with the exponential form which only contains the digits 0 and 2.

For each case, the input file contains a positive integer n (n<=20000).
输出描述:
For each case, you should output the exponential form of n an a single line.Note that,there should not be any additional white spaces in the line.
示例1
输入
1315
输出
2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)

该形式只包括数字2和数字0
这道题在理解起来难度并不大，但是在输出格式上调整了很长时间。

#include 
#include 
#include 
using namespace std;

void dfs(int n){
    vector<int> bin;
    //逆序处理
    while(n){
        bin.push_back(n % 2);
        n /= 2;
    }
    //诸位处理
    bool first = true;
    for (int i = bin.size() - 1; i >= 0;i--){//逆序 从最高位开始
        if(bin[i]==1){//不是第一个元素非0元素
            if(!first){//对于每个指数二进制遍历的最高位 都不需要+
                cout << "+";
            }
            first = false;
            if(i==0){
                cout << "2(0)";
            }else if(i==1){
                cout << "2";
            }else{
                cout << "2(";
                dfs(i);//对指数进行处理
                cout << ")";
            }
        }
        
    }
}
int main(){
    int n;
    while(cin>>n){
        dfs(n);
        cout << "\n";
    }
}