【小白笔记】目标跟踪BACF(Learning Background-Aware Correlation Filters for Visual Tracking)论文笔记
文章目录
- 1.主要贡献
- 2.主要思想
- 2.1思路理解
- 2.2公式表达
- 3.优化方法
- 4.实验结果
1.主要贡献
这篇文章发表于ICCV17上,?论文地址,?项目地址,从思路来说并不难,难的是那个公式化的那个步骤不容易理解,这也是作者的厉害之处,数学表达能力特别强。下面就来说一下这篇文章吧,有不对的地方欢迎一起讨论~
贡献1:这个算法使用了真实的移位产生的负样本,这些样本包括了更大的搜索区域和真实的背景,而不是传统CF方法的由正样本循环移位生成的负样本;
贡献2:提出了一种基于ADMM的方法使该滤波器应用多通道特征比如HOG,同时计算量比较小O(TKL),T是模板拉直后的尺度,K是特征通道数,L是ADMM迭代的次数。
2.主要思想
2.1思路理解
这个算法的思路很好理解,CF类方法的优点是循环样本和快速计算,缺点也是循环样本,这带来了边界效应,我们只能使用有限的搜索域,否则背景的影响将增大影响训练结果,SRDCF就是收到这个启发,对背景部分的滤波器加了惩罚系数,从而可以在更大的搜索域上进行跟踪。但是SRDCF太慢了,且代码很难复现(源码很难懂),对调参能力有很高要求。所以我们为什么不直接用真实的负样本用更大的搜索域试试呢,但是还要保证样本是循环的,怎么办呢,补零就行了,提取一个更大搜索域的样本,用这个样本循环,把除了中间那部分都填上零,相当于我们只关注循环样本的中间一小块,这一小块的大小可以相当于我们原来CF方法的搜索域,这样一来我们不就是既扩大了搜索域又使用了真实的样本同时保证了样本的循环结构吗,思路很简单,数学语言写出来可不容易,看看作者怎么做的。
2.2公式表达
先看一个CF的基础公式
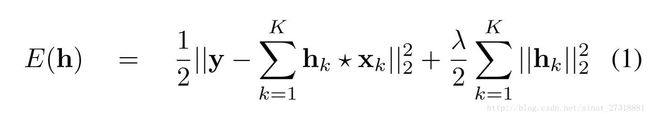
这是单个样本的形式,当我们使用D个循环样本的时候(D也是这个样本的size)则变为如下形式
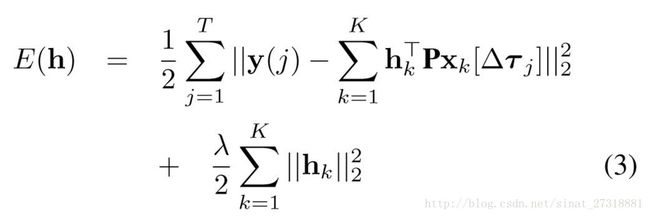
作者使用了一个循环操作符,我文章中写成更简洁的 x k j {\bf{x}}_k^j xkj,代表第j个循环移位样本的第k个通道特征。下面作者就开始他的表演了,就像前面说的,我们需要更多的来自背景的真实样本。首先样本X的大小由D 变大 为T,扩大了很多,用这个大样本生成循环样本,然后我们需要提取中间那部分size为D的部分,这一步作者用一个P矩阵代替,P是一个D×T的二值(0和1)矩阵,1的部分对应大样本的中间那块,这个P可以提前计算出来,是个常数矩阵。那么Px就是D×1的向量了和原来一样。
下面一步很难理解,利用了循环样本的频域快速求解的特性,将表达式变换到频域上,公式如下:

我们来分析一下这个式子怎么来的,首先明确一个一维信号 α \alpha α的离散傅里叶变换表示为 α ^ = T F α \hat{\alpha}=\sqrt{T}\bf{F\alpha} α^=TFα,其中 F \bf{F} F是T×T大小的正交傅里叶变换矩阵。把滤波模板h和矩阵P合起来看成一个新的滤波器 g k = P ⊤ h k g_k=P^{\top}h_k gk=P⊤hk,用这个来代替(2)式中的h(注意 P P T = I PP^T=I PPT=I),然后把通道数k去掉,写成更简洁的形式,那么y后面那一坨就变成 x j ⊤ g {{\bf{x}}^j}^{\top}g xj⊤g,其中g是KT×1大小的, g = ( P ⊤ ⨂ I k ) h g=(P^{\top}\bigotimes I_k)h g=(P⊤⨂Ik)h,其中 h = [ h 1 ⊤ , h 2 ⊤ , . . . , h k ⊤ ] ⊤ h=[h_1^\top,h_2^\top,...,h_k^\top]^{\top} h=[h1⊤,h2⊤,...,hk⊤]⊤这一步可能直积有人不理解,你把它展开就知道了,只要明确每个参数的维度就不会错了, x j = [ x 1 j ⊤ , x 2 j ⊤ , . . . , x k j ⊤ ] ⊤ {{\bf{x}}^j}=[{{\bf{x}}^j_1}^\top,{{\bf{x}}^j_2}^\top,...,{{\bf{x}}^j_k}^\top]^\top xj=[x1j⊤,x2j⊤,...,xkj⊤]⊤,然后再去掉外面那个求和符号,把所有样本都写在一起,那么 y = [ y ( 1 ) , y ( 2 ) , . . . , y ( T ) ] ⊤ y=[y(1),y(2),...,y(T)]^\top y=[y(1),y(2),...,y(T)]⊤, X = [ x 1 , x 2 , . . . , x T ] ⊤ \bf{X}=[{\bf{x}}^1,{\bf{x}}^2,...,{\bf{x}}^T]^\top X=[x1,x2,...,xT]⊤,前面那部分就变成了 y − X g y-{\bf{X}}g y−Xg,你看看维数是不是正确的,显然X是多通道的循环样本构成的矩阵,也可以写成 X = [ X 1 ⊤ , X 2 ⊤ , . . . , X k ⊤ ] \bf{X}=[\bf{X}_1^\top,\bf{X}_2^\top,...,\bf{X}_k^\top] X=[X1⊤,X2⊤,...,Xk⊤],即每个通道的样本的循环矩阵的合并表示形式,每一个 X i ⊤ \bf{X}_i^\top Xi⊤的每一行表示一个样本,由循环样本的性质可以写成
X i ⊤ = F d i a g ( x i ^ ) F H = F H d i a g ( x i ^ ) ⊤ F \bf{X}_{i}^{\top}={\bf{F}}diag(\hat{x_i}){\bf{F}}^H={\bf{F}}^{H}diag(\hat{x_i})^{\top}{\bf{F}} Xi⊤=Fdiag(xi^)FH=FHdiag(xi^)⊤F
那么对Xg进行傅里叶变换则为 T F [ F H d i a g ( x 1 ^ ) ⊤ F , F H d i a g ( x 2 ^ ) ⊤ F , . . . , F H d i a g ( x k ^ ) ⊤ F ] ( P ⊤ ⨂ I k ) h \sqrt{T}\bf{F}[{\bf{F}}^{H}diag(\hat{x_1})^{\top}{\bf{F}},{\bf{F}}^{H}diag(\hat{x_2})^{\top}{\bf{F}},...,{\bf{F}}^{H}diag(\hat{x_k})^{\top}{\bf{F}}](P^{\top}\bigotimes I_k)h TF[FHdiag(x1^)⊤F,FHdiag(x2^)⊤F,...,FHdiag(xk^)⊤F](P⊤⨂Ik)h = [ d i a g ( x 1 ^ ) ⊤ , d i a g ( x 2 ^ ) ⊤ , . . . , d i a g ( x k ^ ) ⊤ ] T ( F P ⊤ ⨂ I k ) h =[diag(\hat{x_1})^{\top},diag(\hat{x_2})^{\top},...,diag(\hat{x_k})^{\top}]\sqrt{T}({\bf{F}}P^{\top}\bigotimes I_k)h =[diag(x1^)⊤,diag(x2^)⊤,...,diag(xk^)⊤]T(FP⊤⨂Ik)h,怎么样是不是得到了文中的表达式了。文中令 g ^ = T ( F P ⊤ ⨂ I k ) h \hat{g}=\sqrt{T}({\bf{F}}P^{\top}\bigotimes I_k)h g^=T(FP⊤⨂Ik)h即所得,并把这个看作一个约束。
3.优化方法
看懂上面一节这里就不难了,主要是优化求解,利用增广拉格朗日乘子法(ALM)将约束项放到优化函数里,如下

然后对g和h进行分别优化求解如下


h的求解有个错误, λ \lambda λ的系数应为1/T。其中一些表达方法的替换这里就不罗嗦了,然后由于离散傅里叶变换后的每个值是相互独立的,所以对每个值分别求解可以大大降低求解g时的速度,就变成求解T个子问题,求g的复杂度变为 O ( T K 3 ) O(TK^3) O(TK3)。
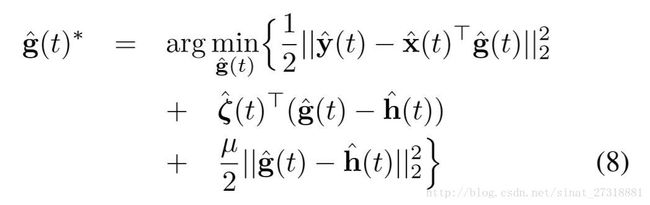

然后看到有一步求逆是复杂度大的原因,这里再次使用求逆引理公式简化公式如下,复杂度变为 O ( T K ) O(TK) O(TK)

然后就是迭代求解了。
4.实验结果
主要看一下速度,达到了35.3fps,是SRDCF的十倍,成功率方面在OTB50达到了67.78%,OTB100达到了62.98%。可以看到一个好的方法一半靠想法一半靠优化。
欢迎讨论~