现代控制理论-4PhasePortrait爱情中的数学
这一章也是我最先看到进而关注up主的一章,特别推荐看原视频(https://www.bilibili.com/video/av15795540 )。我感觉我记下的笔记应该不如原视频精彩的十分之一。
先看一些基本的假设,假设有一个男孩叫与非,女孩叫梦寒。
用 Y ( t ) Y(t) Y(t)表示与非对梦寒的爱或者恨,当 Y > 0 Y>0 Y>0的时候,与非是爱着梦寒的;当 Y < 0 Y<0 Y<0的时候,与非是恨着梦寒的。
同理,梦寒也是一样,用 M ( t ) M(t) M(t)表示梦寒对与非的爱或者恨,当 M > 0 M>0 M>0的时候,梦寒是爱着与非的;当 M < 0 M<0 M<0的时候,梦寒是恨着与非的。
case 1
先看第一种情况
Y ˙ = a M \dot{Y} = aM Y˙=aM
M ˙ = − b Y \dot{M} = -bY M˙=−bY
已知 a , b > 0 a,b>0 a,b>0,可以得出平衡点为 Y f = 0 , M f = 0 Y_f=0,M_f=0 Yf=0,Mf=0,在进行分析之前,我们先来描述一下这个系统。
step1:系统描述
(1)根据这个函数表达式,可以看出与非是个耿直boy,你对我好,我也对你好;你讨厌我,我也不理你。也就是投桃报李+以牙还牙的性格
(2)梦寒则是一个多情的girl,你越热情她越远离;你越冷淡她越着迷,是欲迎还拒+若即若离的性格
step2:计算
我们把这个系统写成状态方程的形式
[ Y ˙ M ˙ ] = [ 0 a − b 0 ] [ Y M ] \left[ \begin{matrix} \dot{Y} \\ \dot{M} \end{matrix}\right] =\left[ \begin{matrix} 0 & a \\ -b & 0 \end{matrix}\right] \left[ \begin{matrix} Y \\ M \end{matrix}\right] [Y˙M˙]=[0−ba0][YM]
通过前面的讲解我们知道可以通过求 A A A矩阵的特征值和特征向量来判断系统的表现,在此,我们求矩阵的特征值,令 A A A矩阵的行列式为0,也就是 ∣ λ I − A ∣ = 0 |\lambda I-A|=0 ∣λI−A∣=0,可以求出 λ = ± a b i \lambda=\pm\sqrt{ab}i λ=±abi。我们知道这是一个center,在直角坐标系中可以表示成一个圆。
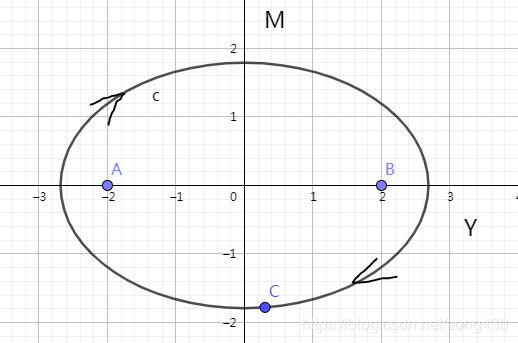
step3:分析
我们可以看出这是一个无限循环,爱恨交织的世界。我们来看第四象限,当 Y > 0 Y>0 Y>0时, M < 0 M<0 M<0,同时 Y ˙ < 0 \dot{Y}<0 Y˙<0,说明与非的热情在减少当中,当移动到临界点的时候,与非开始讨厌梦寒了,此时 Y < 0 Y<0 Y<0, M ˙ > 0 \dot{M}>0 M˙>0,也就是梦寒对与非的状态发生了改变,然后到了第二象限,梦寒开始喜欢与非了( M > 0 M>0 M>0),而随着梦寒的亲近,与非的热情又被点燃了起来,直到某一刻(进入第一象限),与非又开始喜欢梦寒了,但此时的梦寒呢,又受不了与非的热情,开始变得冷淡了起来,他们就这样无限循环,爱恨交织下去。
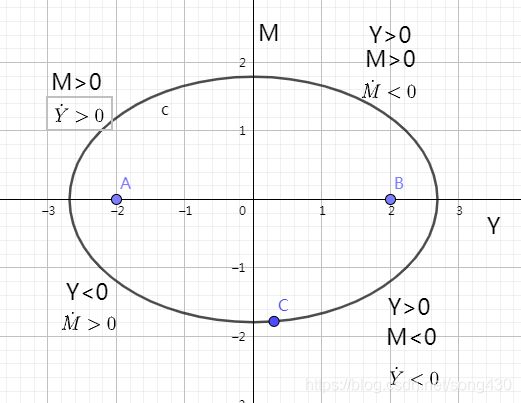
step4:讨论
他们有1/4的时间相爱,1/2的时间是一半火焰,一半海洋,1/4的时间是互相看不顺眼。在这1/4看不顺眼的时间内,up主的原话是“离别不过是另一种方式的陪伴,这一刻让我凝望你的眼”。
case 2
再看另一种情况
Y ˙ = − a Y + b M \dot{Y} = -aY+bM Y˙=−aY+bM
M ˙ = b Y − a M \dot{M} = bY-aM M˙=bY−aM
同样 a , b > 0 a,b>0 a,b>0,可以看出平衡点也都是0。
step1:系统描述
可以看出 Y , M Y,M Y,M是一类人,他们都会积极的回应对方(对别人都是正值, b > 0 b>0 b>0),同时他们都很小心,都有所保留(对自己都是负值, − a < 0 -a<0 −a<0)。
step2:计算
这个时候的 A A A矩阵为
A = [ − a b b − a ] A = \left[ \begin{matrix} - a & b \\ b &-a \end{matrix}\right] A=[−abb−a]
可以计算出特征值为 λ 1 = − a + b , λ 2 = − a − b \lambda_1 = -a+b, \lambda_2 = -a-b λ1=−a+b,λ2=−a−b,特征向量为 v 1 = [ 1 , 1 ] , v 2 = [ 1 , − 1 ] v_1 = [1, \ 1], \ v_2 = [1, \ -1] v1=[1, 1], v2=[1, −1]
step3:分析
我们可以分成两种情况讨论
- case2.1 ∣ a ∣ > ∣ b ∣ |a|>|b| ∣a∣>∣b∣,此时 λ 1 < 0 , λ 2 < 0 \lambda_1<0,\ \lambda_2<0 λ1<0, λ2<0
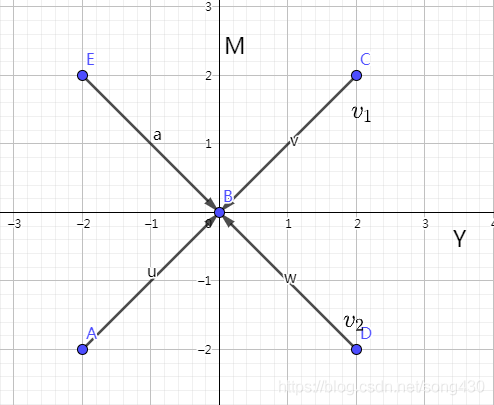
这是一个sink点,随着时间t趋近于无穷, Y Y Y和 M M M终将会变成路人。up主说“十年之后,我们是朋友,还可以问候,却再也找不到拥抱的理由”。 - case2.2 ∣ a ∣ < ∣ b ∣ |a|<|b| ∣a∣<∣b∣,此时 λ 1 > 0 , λ 2 < 0 \lambda_1>0, \ \lambda_2<0 λ1>0, λ2<0
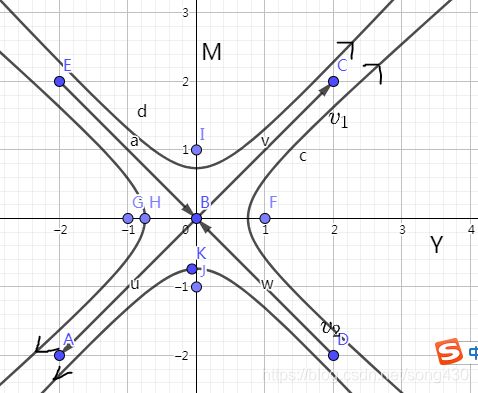
这是一个saddle点,他们或者在第一象限共浴爱河,或者在第三象限变成仇敌,这和他们的初始状态有关,也就是和“第一印象”有关,比如说在第四象限 v 2 v_2 v2向量上方的一点相遇,此时 Y > 0 , M < 0 Y>0,M<0 Y>0,M<0,与非深爱着梦寒,梦寒却有点讨厌与非,在之后的交往中,梦寒逐渐升温(M变大),与非虽然动摇过(Y先减小后增大),但却一直爱着她,这样,终于突破临界点,两个人开始过上了幸福的生活。
如果说说在第四象限 v 2 v_2 v2向量下方的一点相遇,此时 Y > 0 , M < 0 Y>0,M<0 Y>0,M<0,与非深爱着梦寒,梦寒非常讨厌与非,在之后的交往中,梦寒逐渐升温,但与非在交往中坚持不了崩溃了,最后两人形同陌路。
step4:讨论
我们来讨论一下这两种结果,当 ∣ a ∣ > ∣ b ∣ |a|>|b| ∣a∣>∣b∣的时候,我们实际上在说一个人的自我意识要大于对对方的感受,最后两个人要变成路人, ∣ a ∣ < ∣ b ∣ |a|<|b| ∣a∣<∣b∣的时候,是说对对方的感受要大于自我意识,这时候会有两种结果,要么共浴爱河,要么因爱生恨。这就验证了很多人宁愿做朋友,也不愿意去打破平衡,也说明了你不认真肯定是赢不了的,但认真的话你可能就输了。