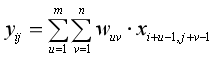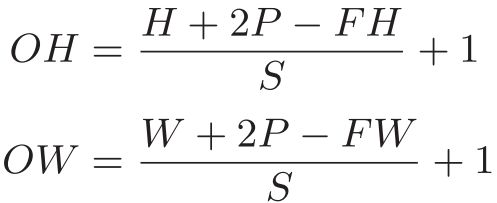卷积神经网络(CNN)因为在图像识别任务中大放异彩,而广为人知,近几年卷积神经网络在文本处理中也有了比较好的应用。我用TextCnn来做文本分类的任务,相比TextRnn,训练速度要快非常多,准确性也比较高。TextRnn训练慢得像蜗牛(可能是我太没有耐心),以至于我直接中断了训练,到现在我已经忘记自己到底有没有成功训练一只TextRnn了。
卷积神经网络可以说是非常优美了,卷积操作(局部连接和权值共享)和池化操作,极大地减少了模型的参数,大大加快了模型训练的速度,才使得神经网络得以如此大规模的应用。
所以这篇文章好好整理一下有关卷积神经网络的基础知识,暂不涉及TextCnn的内容。
一、卷积神经网络的概念
卷积神经网络(Convolutional Neural Network,CNN)是一种具有局部连接、权值共享以及池化特性的深层前馈神经网络,一般由卷积层、池化层和全连接层交叉堆叠而成(全连接层为顶层)。这三个特性使得卷积神经网络具有一定程度上的平移、缩放和旋转不变性,可以提取到自然图像中的局部不变特征,并且参数相比全连接前馈神经网络要少很多,易于训练。
在理解卷积神经网络的结构之前,先了解卷积的概念。
1、卷积的基本操作
卷积(Convolution)是分析数学中的一种重要运算,因为图像是个二维结构(不考虑通道),所以在图像处理中通常使用二维卷积。滤波器(Filter)也称为卷积核(Convolutional Kernel),经常作为特征提取的有效方法,而一幅图像在经过卷积操作之后得到的结果称为特征映射(Feature Map)。二维卷积核是一个矩阵,如下是一个高斯卷积核,可以对图像进行平滑去噪。
卷积的具体操作是,给定一个图像![]() ,和滤波器
,和滤波器![]() ,一般有m
,一般有m
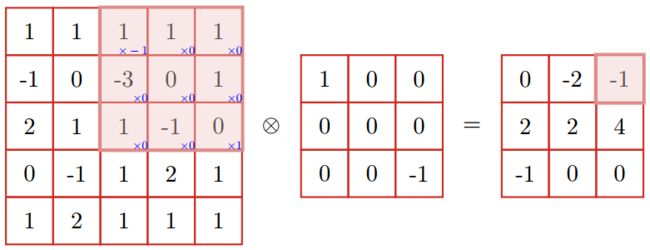
与图形相对照如下,卷积操作就是在一个图像上滑动一个卷积核,通过卷积操作来得到新的特征。
上图中,左边是图像的长和高两个维度x(图像有三个维度,分别为长、高和通道),中间这个矩阵是卷积核w,于是我们看最右边这个矩阵中高亮的元素-1是如何计算出来的。注意卷积运算不是矩阵乘法,而是形状相同的两个矩阵的对应位置元素的乘积之和。也就是:
![]()
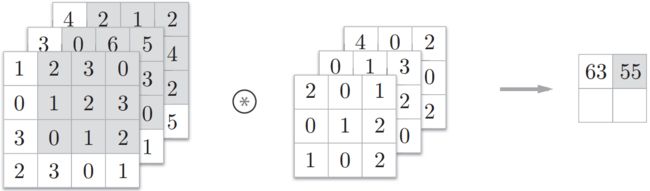
而如果考虑图像的通道的话,那么图像是3维数据,通道数为3,那么就先对每个通道上的输入数据和滤波器进行卷积运算,然后再把3个通道的卷积结果相加,得到输出。
2、卷积的步长和零填充
在卷积基本操作的基础上,还可以引入卷积核的滑动步长(Stride)和零填充(Zero Padding)来增加卷积的多样性,可以更灵活地进行特征提取。
卷积核的步长是指卷积核在滑动时的时间间隔,下图为一维卷积中步长为2的例子,一维卷积核取[1, 0, -1]。
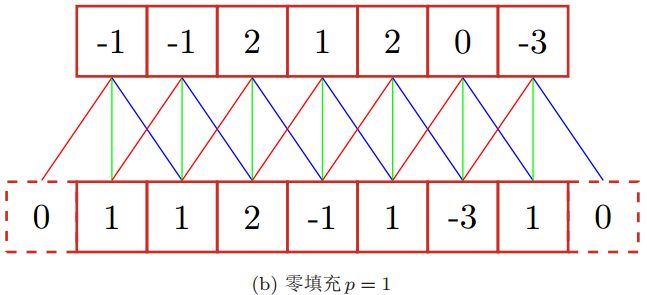
零填充则是在输入向量或者输入矩阵周围补零。为什么需要补零呢?原因是步长大于1时,对输入数据向右卷积的过程中可能会产生最后一个卷积块不完整的问题。此外,使用零填充更主要是为了调整输出的大小,实现输出空间大小不变的情况下将输出传入下一层。因为如果每次卷积过后输出的空间都缩小,那么在某个时刻输出的大小可能变为1,就无法再进行卷积了。下图是一维卷积中零填充的示例,一维卷积核取[1, 0, -1]。
假设卷积层的输入大小为(H, W),输入层神经元个数为H;卷积核大小为(FH, FW),步长为s,填补为p,输出大小为(OH, OW),那么该卷积层的输出的大小可以这样计算:
特别的,当步长为1,两端不补零时(p=0),卷积层的输出大小为(H-FH+1, W-FW+1),其中(H-FH+1)是卷积层神经元的个数。
二、卷积神经网络的结构和特性
卷积神经网络一般由卷积层、池化层和全连接层构成。
(一)卷积层
1、用卷积代替全连接
在全连接前馈神经网络中,如果第l层有n(l)个神经元,第l-1层有n(l-1)个神经元,则权重矩阵有n(l)×n(l-1)个参数,参数的数量太大。
如果用卷积来替代全连接,第l层的净输入z(l)为第l-1层活性值a(l-1)和卷积核w(l)的卷积,那么经过卷积操作可以得到:
卷积操作有两个重要的性质。
一是局部连接。在卷积层(假设为第l层)中每个神经元都只与下一层(第l-1层)中的某个滑动窗口中的神经元相连接,构成一个局部连接网络。卷积层和下一层之间的连接数大大减少,由原来的n(l)×n(l-1)个连接变成n(l)×m个连接,m为卷积核的大小。
二是权值共享。作为参数的卷积核w(l)对于第l层中所有的神经元都是相同的。于是卷积层的参数只有一个m维的权重w(l)和1维的偏置b(l),共m+1参数。
另外第l层的神经元个数是由第l-1层的神经元个数和卷积核的大小所决定的,满足:
![]()
卷积神经网络的局部连接和权值共享特性如下图所示:
2、卷积层的作用
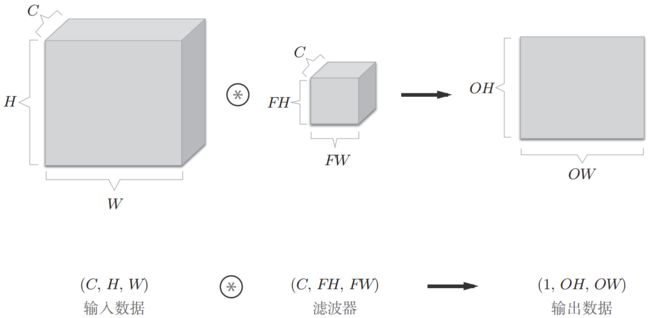
卷积层的作用是提取一个局部区域的特征,不同的卷积核相当于不同的特征提取器。由于图像是三维数据,除了长、高以外,还有通道,于是通常把神经元组织成三维结构的神经层,大小为通道数C×高度H×长度W,即(C, H, W),由C个H×W的特征映射构成。
特征映射是一幅图像经过卷积后提取到的特征,每个特征映射可以作为抽取到的一类图像特征。如果是灰色图像,那么只有一个特征映射,也就是通道数C为1;如果是彩色图像,分别有RGB三个颜色通道,那么有三个特征映射,C=3。
卷积核也一样,大小为通道数C×高度FH×长度FW,即(C, FH, FW)。其中卷积核的通道数必须和输入层的通道数一致,都是C。
如果卷积核只有一个,那么卷积层的输出就是一张特征图,也就是说卷积层输出的通道是1。
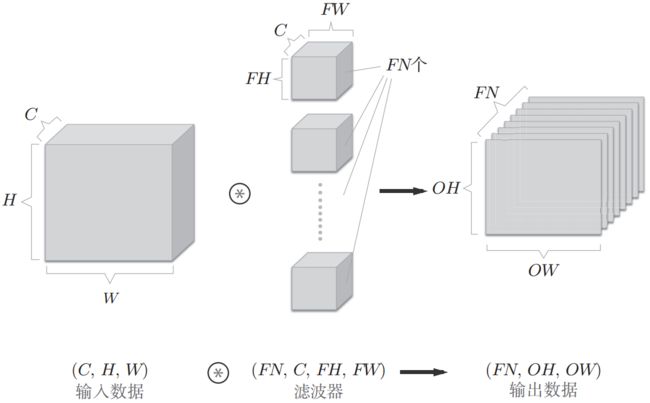
如果希望卷积层的输出也是多通道的,那么就需要就需要用到多个卷积核(权重),比如用FN个卷积核,那么卷积层的输出数据的大小为(FN, OH, OW)。
从上面这个图可以总结出一个规律:输入层的通道数和卷积核的通道数C相等,而卷积核的个数FN与卷积层的通道数FN相等。
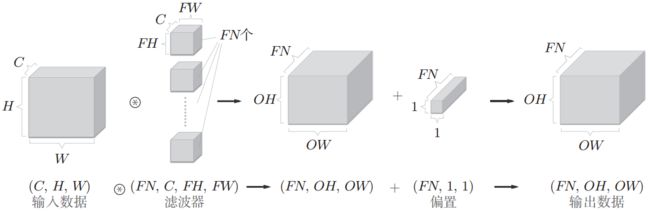
卷积运算中一样存在偏置,偏置中元素的个数和卷积核的个数一致,即卷积层的每个通道有一个偏置值,这些偏置是相等的。如果加上偏置,那么卷积层真正的输出如下图:
(二)池化层
池化层(Pooling Layer)也叫子采样层(Subsampling Layer),它的作用是进行特征选择,降低特征数量,并从而减少参数数量。
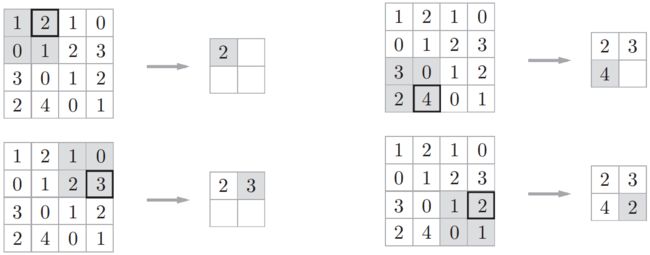
1、最大池化案例
直接来看一个最大池化的例子,一图胜千言。先来看单通道最大池化的过程,取上一层中一个通道的输出数据,是4×4的矩阵,然后将其划分为4个2×2的小矩阵,找出每个小矩阵中的最大值,重新构成一个2×2的矩阵,这就是最大池化后池化层某个通道的输出结果。这里池化层也可以看做是一个特殊的卷积层,卷积核大小为 2 × 2,步长为 2 ,卷积核为 max函数。
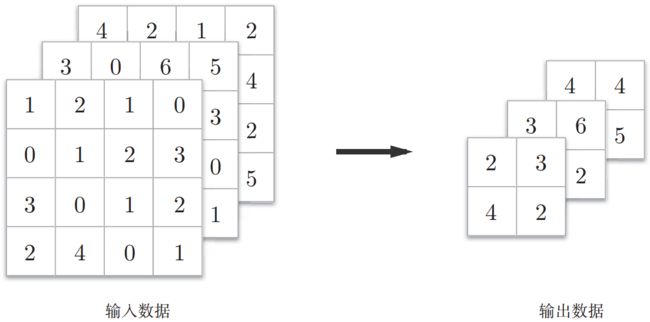
再来看多通道最大池化的过程,也就是在每个通道上都进行上一步,得到的最大池化输出也是3个通道的,也就是说在最大池化过程中,通道数不变。
2、池化的理论说明
接下来我们再从理论的高度来阐述一下池化。
卷积层尽管可以显著减少网络中的连接数量,但是如果经过零填充操作,则神经元的个数并没有显著减少,如果后面接一个分类器,则输入的特征维度仍然很高,容易造成过拟合。因此可以在卷积层后面加一个池化层,从而降低特征维度并保留有效信息,避免过拟合。此外,池化层还可以保持图像的旋转、平移和伸缩的不变性,并且提高计算速度。
池化是这样做的,首先把上一层的输出数据(一个矩阵)划分为多个区域![]() ,一般会把池化窗口的大小设定为和步长一样大,那么区域就是不重叠的。
,一般会把池化窗口的大小设定为和步长一样大,那么区域就是不重叠的。
然后池化就是指对每个区域进行下采样(Down Sampling),得到一个值作为该区域的概括。通过下采样,可以缩小图像,比如对于一副尺寸为M×N的图像,对其进行s倍下采样,即得到(M/s)×(N/s)尺寸的分辨率图像。
而常见的池化有两种,一种是最大池化(Max Pooling),即从目标区域中取出最大值;另一种是平均池化(Average Pooling),即计算目标区域中的最大值。在图像处理中,主要用到最大池化。
3、池化层的特性
池化层有三个特性:
(1)没有需要学习的参数
池化层和卷积层不同,没有需要学习的参数,而只是从目标区域中取出最大值或平均值。
(2)通道数不发生变化
经过池化运算,输入数据和输出数据的通道数不会发生变化,计算是按照通道独立进行的。
(3)对微小的变化具有鲁棒性
在最大池化中,输入数据发生微小偏差时,池化仍然会返回相同的结果,因此对输入数据的微小偏差具有鲁棒性。
(三)卷积神经网络的典型结构
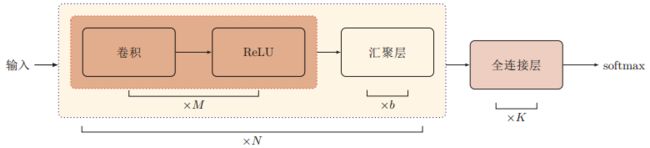
经过多轮卷积层、池化层的交叉堆叠后之后,就要接全连接层输出结果了。目前常用的卷积神经网络结构图如下。一个卷积块由连续M(M取2~5)个卷积层和b(b取0或1)个池化层构成。这种结构的卷积神经网络在堆叠了N(N取1~100都有可能)个连续的卷积块之后,连接K个全连接层(K一般取0~2)。
而最具代表性的两个卷积神经网络结构是LeNet和AlexNet,这两个神经网络的结构图就不贴上来了,主要说明一下两个网络大致的特点。
LeNet使用连续的卷积层和子采样层(Sub Sampling),最后接全连接层输出结果。和现在的CNN相比,它的特点在于:一是使用Sigmoid激活函数,而现在的CNN主要使用ReLU函数;二是使用子采样缩小中间数据的大小,用到的是平均池化,而现在的CNN使用最大池化是主流。
AlexNet的网络结构和LeNet基本没有什么不同,也是叠加多个卷积层和池化层(不过这里是最大池化),最后经全连接层输出结果。但AlexNet和LeNet有以下几点差异:一是激活函数使用ReLU函数;二是使用了dropout避免过拟合;三是使用了数据增强技术;四是使用了最大池化。
三、卷积神经网络的参数学习
在卷积神经网络中,主要有两种不同功能的神经层:卷积层和池化层。由于池化层中没有参数,所以卷积神经网络的参数为卷积核中的权重以及偏置。
卷积神经网络是前馈神经网络的一种,与全连接的前馈神经网络类似,卷积神经网络也可以通过误差反向传播来进行参数学习,也就是要计算每一个卷积层的误差项δ,进行反向传播,并进一步计算每一个卷积层参数的梯度,用来更新权重和偏置。
计算公式过于复杂,我就不推导了,到此为止。
四、碎碎念
用邱锡鹏老师的书整理多篇笔记了,我必须安利一波啊!如果有人认真看了我的笔记(真的只是读书笔记),又看了邱老师的书,就会发现我基本就是在摘录邱老师的书(初学者只能这样做笔记啦)。这也不能怪我,因为邱老师的书实在太干了:干货太多了,我都没法自己总结了!
看邱老师的书,有种看李航老师的《统计学习方法》的感觉,内容精悍而不失丰富性,数学公式优美,推导清晰。如果你在看吴恩达老师的深度学习课程,觉得讲得太琐碎、例子太多时,那么邱老师的书是你梳理知识和整理笔记的不二之选。
但是看得出邱老师过于痴迷于数学表达了,其实卷积神经网络还是多以图形的方式来阐述比较好,所以搭配其他资料进行学习也是必要的。
参考资料:
1、邱锡鹏:《神经网络与深度学习》
2、斋藤康毅 :《深度学习入门 : 基于Python的理论与实现 》