一、求传递函数
1.已知系统的零点、极点和零极点增益,求系统的传递函数。
G=zpk([],[0,-1,-2],4)
Zero/pole/gain:
4
-------------
s (s+1) (s+2)
2.已知传递函数的分子和分母多项式系数,求系统传递函数。
num=4;
den=conv([1 1 0],[1 2]);
G=tf(num,den)
Transfer function:
4
-----------------
s^3 + 3 s^2 + 2 s
二、状态方程描述的系统模型
根据状态方程的4个系数矩阵A、B、C、D
A=[-2,0,1;0,-1,0;0,1,0];
B=[0;2;0];
C=[2,0,0];
D=0;
G=ss(A,B,C,D)
a =
x1 x2 x3
x1 -2 0 1
x2 0 -1 0
x3 0 1 0
b =
u1
x1 0
x2 2
x3 0
c =
x1 x2 x3
y1 2 0 0
d =
u1
y1 0
Continuous-time model.
三、不同模型之间的互换
1.
G1=zpk([],[0,-1,-2],4)%模型一
G2=ss(G1)%模型二
Zero/pole/gain:
4
-------------
s (s+1) (s+2)
a =
x1 x2 x3
x1 0 1 0
x2 0 -1 1
x3 0 0 -2
b =
u1
x1 0
x2 0
x3 2
c =
x1 x2 x3
y1 2 0 0
d =
u1
y1 0
Continuous-time model.
2.
A=[-2,0,1;0,-1,0;0,1,0];
B=[0;2;0];
C=[2,0,0];
D=0;
G1=ss(A,B,C,D) %模型一
G2=tf(G1)%模型二
a =
x1 x2 x3
x1 -2 0 1
x2 0 -1 0
x3 0 1 0
b =
u1
x1 0
x2 2
x3 0
c =
x1 x2 x3
y1 2 0 0
d =
u1
y1 0
Continuous-time model.
Transfer function:
4
-----------------
s^3 + 3 s^2 + 2 s
四、建立复杂的数学模型
对于一个负反馈系统,其前向通道由G1和G2串联而成,反馈通道用H表示
G1=tf([1 7 24 24],[1 10 35 50 24]);
G2=tf([10,5],[1,0]);
H=tf([1],[0.01,1]);
Gc=feedback(G1*G2,H)
Transfer function:
0.1 s^5 + 10.75 s^4 + 77.75 s^3 + 278.6 s^2 + 361.2 s + 120
------------------------------------------------------------------
0.01 s^6 + 1.1 s^5 + 20.35 s^4 + 110.5 s^3 + 325.2 s^2 + 384 s + 120
五、稳定性分析
找出该系统所有的极点,看是否有实部大于或等于0的极点。
1.
G1=tf([1 7 24 24],[1 10 35 50 24]);
eig(G1)%方法一
roots(G1.den{1})%方法一
G2=zpk(G1);
G2.p{1}%方法一
ans =
-4.0000
-3.0000
-2.0000
-1.0000
ans =
-4.0000
-3.0000
-2.0000
-1.0000
ans =
-4.0000
-3.0000
-2.0000
-1.0000
2.
G=zpk([],[0 -1 -2],4);%4为开环增益
Gc=feedback(G,1);
pole(Gc)
ans =
-2.7963
-0.1018 + 1.1917i
-0.1018 - 1.1917i
当开环增益取8时,系统变得不稳定
ans =
0.0832 + 1.5874i
0.0832 - 1.5874i
-3.1663
说明开环增益越大,闭环系统越不稳定。
六、求解时域响应
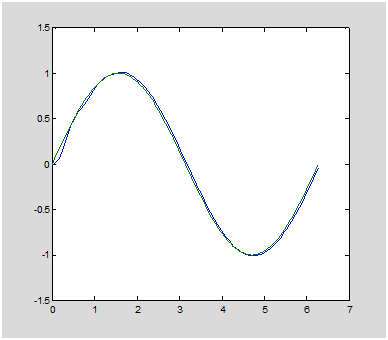
1.
G=tf(100,[1 4 100]);
t=0:pi/50:2*pi;
u=sin(t);
y=lsim(G,u,t);
plot(t,y,t,u)
2.
step(G)%单位阶跃响应
3.
impulse(G) %单位脉冲响应
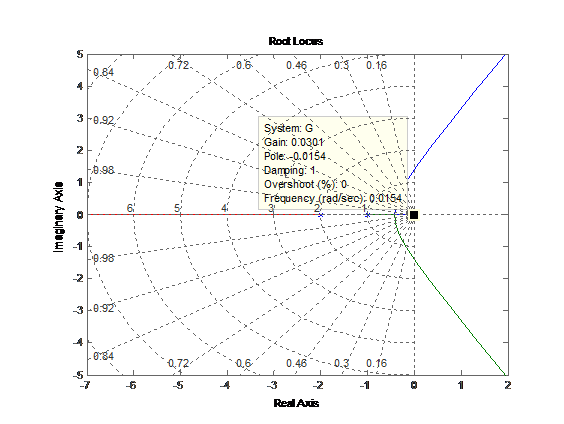
七、根轨迹分析
1.
G=zpk([],[0 -1 -2],1);
rlocus(G)
2.
G=tf(1,[conv([1,3],[1,2,2]),0]);
rlocus(G)