数据结构算法之二——几种基本数据结构总结
转载自YSOcean数据结构与算法系列的博客
而本篇博客讲解的数据结构和算法更多是用作程序员的工具,它们作为构思算法的辅助工具,而不是完全的数据存储工具。这些数据结构的生命周期比数据库类型的结构要短得多,在程序执行期间它们才被创建,通常用它们去执行某项特殊的业务,执行完成之后,它们就被销毁。这里的它们就是——栈、队列、链表。
栈
- 基本概念:又称为堆栈或堆叠,栈作为一种数据结构,是一种只能在一端进行插入和删除操作的特殊线性表。它按照先进后出的原则存储数据,先进入的数据被压入栈底,最后的数据在栈顶,需要读数据的时候从栈顶开始弹出数据(最后一个数据被第一个读出来)。栈具有记忆作用,对栈的插入与删除操作中,不需要改变栈底指针。
- JAVA实现:
public class MyStack {
private int[] array;
private int maxSize;
private int top;
public MyStack(int size){
this.maxSize = size;
array = new int[size];
top = -1;
}
//压入数据
public void push(int value){
if(top < maxSize-1){
array[++top] = value;
}
}
//弹出栈顶数据
public int pop(){
return array[top--];
}
//访问栈顶数据
public int peek(){
return array[top];
}
//判断栈是否为空
public boolean isEmpty(){
return (top == -1);
}
//判断栈是否满了
public boolean isFull(){
return (top == maxSize-1);
}
}程序解释:这个栈是用数组实现的,内部定义了一个数组,一个表示最大容量的值以及一个指向栈顶元素的top变量。构造方法根据参数规定的容量创建一个新栈,push()方法是向栈中压入元素,指向栈顶的变量top加一,使它指向原顶端数据项上面的一个位置,并在这个位置上存储一个数据。pop()方法返回top变量指向的元素,然后将top变量减一,便移除了数据项。要知道 top 变量指向的始终是栈顶的元素。
产生的问题:
①、上面栈的实现初始化容量之后,后面是不能进行扩容的(虽然栈不是用来存储大量数据的),如果说后期数据量超过初始容量之后怎么办?(自动扩容)
②、我们是用数组实现栈,在定义数组类型的时候,也就规定了存储在栈中的数据类型,那么同一个栈能不能存储不同类型的数据呢?(声明为Object)
③、栈需要初始化容量,而且数组实现的栈元素都是连续存储的,那么能不能不初始化容量呢?(改为由链表实现)
- 解决1,2问题
public class ArrayStack {
//存储元素的数组,声明为Object类型能存储任意类型的数据
private Object[] elementData;
//指向栈顶的指针
private int top;
//栈的总容量
private int size;
//默认构造一个容量为10的栈
public ArrayStack(){
this.elementData = new Object[10];
this.top = -1;
this.size = 10;
}
public ArrayStack(int initialCapacity){
if(initialCapacity < 0){
throw new IllegalArgumentException("栈初始容量不能小于0: "+initialCapacity);
}
this.elementData = new Object[initialCapacity];
this.top = -1;
this.size = initialCapacity;
}
//压入元素
public Object push(Object item){
//是否需要扩容
isGrow(top+1);
elementData[++top] = item;
return item;
}
//弹出栈顶元素
public Object pop(){
Object obj = peek();
remove(top);
return obj;
}
//获取栈顶元素
public Object peek(){
if(top == -1){
throw new EmptyStackException();
}
return elementData[top];
}
//判断栈是否为空
public boolean isEmpty(){
return (top == -1);
}
//删除栈顶元素
public void remove(int top){
//栈顶元素置为null
elementData[top] = null;
this.top--;
}
/**
* 是否需要扩容,如果需要,则扩大一倍并返回true,不需要则返回false
* @param minCapacity
* @return
*/
public boolean isGrow(int minCapacity){
int oldCapacity = size;
//如果当前元素压入栈之后总容量大于前面定义的容量,则需要扩容
if(minCapacity >= oldCapacity){
//定义扩大之后栈的总容量
int newCapacity = 0;
//栈容量扩大两倍(左移一位)看是否超过int类型所表示的最大范围
if((oldCapacity<<1) - Integer.MAX_VALUE >0){
newCapacity = Integer.MAX_VALUE;
}else{
newCapacity = (oldCapacity<<1);//左移一位,相当于*2
}
this.size = newCapacity;
int[] newArray = new int[size];
elementData = Arrays.copyOf(elementData, size);
return true;
}else{
return false;
}
}
}- 总结:根据栈后进先出的特性,我们实现了单词逆序以及分隔符匹配。所以其实栈是一个概念上的工具,具体能实现什么功能可以由我们去想象。栈通过提供限制性的访问方法push()和pop(),使得程序不容易出错。
对于栈的实现,我们稍微分析就知道,数据入栈和出栈的时间复杂度都为O(1),也就是说栈操作所耗的时间不依赖栈中数据项的个数,因此操作时间很短。而且需要注意的是栈不需要比较和移动操作,我们不要画蛇添足。
队列
- 概念:队列(queue)是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。队列中没有元素时,称为空队列。
队列分为:
①、单向队列(Queue):只能在一端插入数据,另一端删除数据。
②、双向队列(Deque):每一端都可以进行插入数据和删除数据操作。
这里我们还会介绍一种队列——优先级队列,优先级队列是比栈和队列更专用的数据结构,在优先级队列中,数据项按照关键字进行排序,关键字最小(或者最大)的数据项往往在队列的最前面,而数据项在插入的时候都会插入到合适的位置以确保队列的有序。
- Java模拟单向队列实现
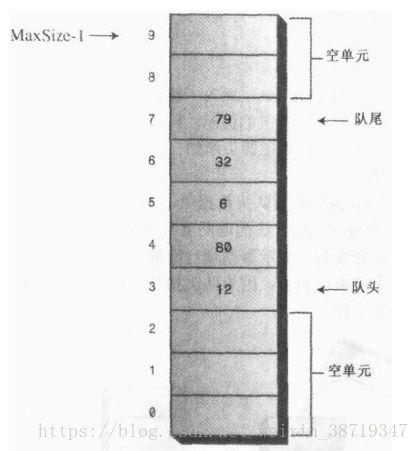
队尾指针可能很快就移动到数据的最末端了,这时候可能移除过数据,那么队头会有空着的位置,然后新来了一个数据项,由于队尾不能再向上移动了,那该怎么办呢?如下图:
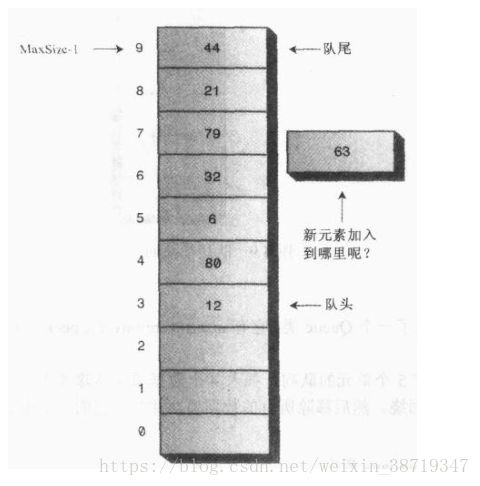
为了避免队列不满却不能插入新的数据,我们可以让队尾指针绕回到数组开始的位置,这也称为“循环队列”。
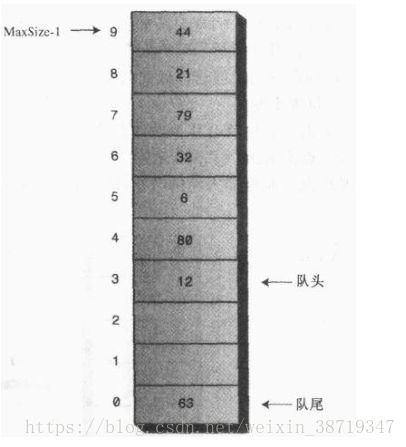
- Java实现代码如下
public class MyQueue {
private Object[] queArray;
//队列总大小
private int maxSize;
//前端
private int front;
//后端
private int rear;
//队列中元素的实际数目
private int nItems;
public MyQueue(int s){
maxSize = s;
queArray = new Object[maxSize];
front = 0;
rear = -1;
nItems = 0;
}
//队列中新增数据
public void insert(int value){
if(isFull()){
System.out.println("队列已满!!!");
}else{
//如果队列尾部指向顶了,那么循环回来,执行队列的第一个元素
if(rear == maxSize -1){
rear = -1;
}
//队尾指针加1,然后在队尾指针处插入新的数据
queArray[++rear] = value;
nItems++;
}
}
//移除数据
public Object remove(){
Object removeValue = null ;
if(!isEmpty()){
removeValue = queArray[front];
queArray[front] = null;
front++;
if(front == maxSize){
front = 0;
}
nItems--;
return removeValue;
}
return removeValue;
}
//查看对头数据
public Object peekFront(){
return queArray[front];
}
//判断队列是否满了
public boolean isFull(){
return (nItems == maxSize);
}
//判断队列是否为空
public boolean isEmpty(){
return (nItems ==0);
}
//返回队列的大小
public int getSize(){
return nItems;
}
}- 优先级队列:优先级队列(priority queue)是比栈和队列更专用的数据结构,在优先级队列中,数据项按照关键字进行排序,关键字最小(或者最大)的数据项往往在队列的最前面,而数据项在插入的时候都会插入到合适的位置以确保队列的有序。
- 数组实现优先级队列,声明为int类型的数组,关键字是数组里面的元素,在插入的时候按照从大到小的顺序排列,也就是越小的元素优先级越高。
- 代码实现:
public class PriorityQue {
private int maxSize;
private int[] priQueArray;
private int nItems;
public PriorityQue(int s){
maxSize = s;
priQueArray = new int[maxSize];
nItems = 0;
}
//插入数据
public void insert(int value){
int j;
if(nItems == 0){
priQueArray[nItems++] = value;
}else{
j = nItems -1;
//选择的排序方法是插入排序,按照从大到小的顺序排列,越小的越在队列的顶端
while(j >=0 && value > priQueArray[j]){
priQueArray[j+1] = priQueArray[j];
j--;
}
priQueArray[j+1] = value;
nItems++;
}
}
//移除数据,由于是按照大小排序的,所以移除数据我们指针向下移动
//被移除的地方由于是int类型的,不能设置为null,这里的做法是设置为 -1
public int remove(){
int k = nItems -1;
int value = priQueArray[k];
priQueArray[k] = -1;//-1表示这个位置的数据被移除了
nItems--;
return value;
}
//查看优先级最高的元素
public int peekMin(){
return priQueArray[nItems-1];
}
//判断是否为空
public boolean isEmpty(){
return (nItems == 0);
}
//判断是否满了
public boolean isFull(){
return (nItems == maxSize);
}
}- 程序解释:insert() 方法,先检查队列中是否有数据项,如果没有,则直接插入到下标为0的单元里,否则,从数组顶部开始比较,利用插入算法,找到比插入值小的位置,该位置之后的后移进行插入,并把 nItems 加1.
- 注意:优先级队列与单向队列的差别在于,优先级队列插入的时候用插入算法插入到大小合适的位置以维护优先级,而remove的的时候,则是按照优先级来,不向单向链表遵守先进先出的规则,即remove优先级低的
见图: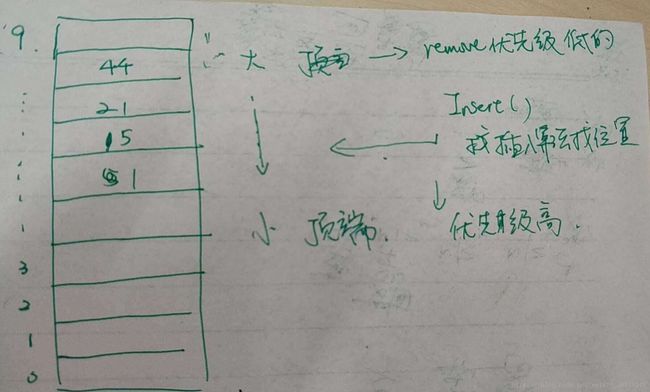
链表
1 package com.ys.datastructure;
2
3 public class SingleLinkedList {
4 private int size;//链表节点的个数
5 private Node head;//头节点
6
7 public SingleLinkedList(){
8 size = 0;
9 head = null;
10 }
11
12 //链表的每个节点类
13 private class Node{
14 private Object data;//每个节点的数据
15 private Node next;//每个节点指向下一个节点的连接
16
17 public Node(Object data){
18 this.data = data;
19 }
20 }
21
22 //在链表头添加元素
23 public Object addHead(Object obj){
24 Node newHead = new Node(obj);
25 if(size == 0){
26 head = newHead;
27 }else{
28 newHead.next = head;
29 head = newHead;
30 }
31 size++;
32 return obj;
33 }
34
35 //在链表头删除元素
36 public Object deleteHead(){
37 Object obj = head.data;
38 head = head.next;
39 size--;
40 return obj;
41 }
42
43 //查找指定元素,找到了返回节点Node,找不到返回null
44 public Node find(Object obj){
45 Node current = head;
46 int tempSize = size;
47 while(tempSize > 0){
48 if(obj.equals(current.data)){
49 return current;
50 }else{
51 current = current.next;
52 }
53 tempSize--;
54 }
55 return null;
56 }
57
58 //删除指定的元素,删除成功返回true
59 public boolean delete(Object value){
60 if(size == 0){
61 return false;
62 }
63 Node current = head;
64 Node previous = head;
65 while(current.data != value){
66 if(current.next == null){
67 return false;
68 }else{
69 previous = current;
70 current = current.next;
71 }
72 }
73 //如果删除的节点是第一个节点
74 if(current == head){
75 head = current.next;
76 size--;
77 }else{//删除的节点不是第一个节点
78 previous.next = current.next;
79 size--;
80 }
81 return true;
82 }
83
84 //判断链表是否为空
85 public boolean isEmpty(){
86 return (size == 0);
87 }
88
用单向链表实现栈:栈的pop()方法和push()方法,对应于链表的在头部删除元素deleteHead()以及在头部增加元素addHead()。相当于链表头部是栈顶。
public class StackSingleLink {
4 private SingleLinkedList link;
5
6 public StackSingleLink(){
7 link = new SingleLinkedList();
8 }
9
10 //添加元素
11 public void push(Object obj){
12 link.addHead(obj);
13 }
14
15 //移除栈顶元素
16 public Object pop(){
17 Object obj = link.deleteHead();
18 return obj;
19 }
20
21 //判断是否为空
22 public boolean isEmpty(){
23 return link.isEmpty();
24 }
25
26 //打印栈内元素信息
27 public void display(){
28 link.display();
29 }
30
31 }- 双端链表:对于单项链表,我们如果想在尾部添加一个节点,那么必须从头部一直遍历到尾部,因为单向想找尾部需要一个Next一个next去找(不是数组 没有下标),找到尾节点,然后在尾节点后面插入一个节点。这样操作很麻烦,如果我们在设计链表的时候多个对尾节点的引用,那么会简单很多。
public class DoublePointLinkedList {
4 private Node head;//头节点
5 private Node tail;//尾节点
6 private int size;//节点的个数
7
8 private class Node{
9 private Object data;
10 private Node next;
11
12 public Node(Object data){
13 this.data = data;
14 }
15 }
16
17 public DoublePointLinkedList(){
18 size = 0;
19 head = null;
20 tail = null;
21 }
22
23 //链表头新增节点
24 public void addHead(Object data){
25 Node node = new Node(data);
26 if(size == 0){//如果链表为空,那么头节点和尾节点都是该新增节点
27 head = node;
28 tail = node;
29 size++;
30 }else{
31 node.next = head;
32 head = node;
33 size++;
34 }
35 }
36
37 //链表尾新增节点
38 public void addTail(Object data){
39 Node node = new Node(data);
40 if(size == 0){//如果链表为空,那么头节点和尾节点都是该新增节点
41 head = node;
42 tail = node;
43 size++;
44 }else{
45 tail.next = node;
46 tail = node;
47 size++;
48 }
49 }
50
51 //删除头部节点,成功返回true,失败返回false
52 public boolean deleteHead(){
53 if(size == 0){//当前链表节点数为0
54 return false;
55 }
56 if(head.next == null){//当前链表节点数为1
57 head = null;
58 tail = null;
59 }else{
60 head = head.next;
61 }
62 size--;
63 return true;
64 }
65 //判断是否为空
66 public boolean isEmpty(){
67 return (size ==0);
68 }
69 //获得链表的节点个数
70 public int getSize(){
71 return size;
72 }
73
双端链表实现队列 即 插入调用addtail(),删除调用deletehead()实现先进先出
1 package com.ys.link;
2
3 public class QueueLinkedList {
4
5 private DoublePointLinkedList dp;
6
7 public QueueLinkedList(){
8 dp = new DoublePointLinkedList();
9 }
10 public void insert(Object data){
11 dp.addTail(data);
12 }
13
14 public void delete(){
15 dp.deleteHead();
16 }
17
18 public boolean isEmpty(){
19 return dp.isEmpty();
20 }
21
22 public int getSize(){
23 return dp.getSize();
24 }
25
26 public void display(){
27 dp.display();
28 }
29
30 }- 有序链表:在有序链表中,数据是按照关键值有序排列的。一般在大多数需要使用有序数组的场合也可以使用有序链表。有序链表优于有序数组的地方是插入的速度(因为元素不需要移动),另外链表可以扩展到全部有效的使用内存,而数组只能局限于一个固定的大小中。
3 public class OrderLinkedList {
4 private Node head;
5
6 private class Node{
7 private int data;
8 private Node next;
9
10 public Node(int data){
11 this.data = data;
12 }
13 }
14
15 public OrderLinkedList(){
16 head = null;
17 }
18
19 //插入节点,并按照从小打到的顺序排列
20 public void insert(int value){
21 Node node = new Node(value);
22 Node pre = null;
23 Node current = head;
24 while(current != null && value > current.data){
25 pre = current;
26 current = current.next;
27 }
28 if(pre == null){
29 head = node;
30 head.next = current;
31 }else{
32 pre.next = node;
33 node.next = current;
34 }
35 }
36
37 //删除头节点
38 public void deleteHead(){
39 head = head.next;
40 }
41
42 public void display(){
43 Node current = head;
44 while(current != null){
45 System.out.print(current.data+" ");
46 current = current.next;
47 }
48 System.out.println("");
49 }
50
51 }注:抽象数据类型(ADT)是指一个数学模型及定义在该模型上的一组操作。它仅取决于其逻辑特征,而与计算机内部如何表示和实现无关。比如刚才说得整型,各个计算机,不管大型机、小型机、PC、平板电脑甚至智能手机,都有“整型”类型,也需要整形运算,那么整型其实就是一个抽象数据类型。
更广泛一点的,比如我们刚讲解的栈和队列这两种数据结构,我们分别使用了数组和链表来实现,比如栈,对于使用者只需要知道pop()和push()方法或其它方法的存在以及如何使用即可,使用者不需要知道我们是使用的数组或是链表来实现的。
ADT的思想可以作为我们设计工具的理念,比如我们需要存储数据,那么就从考虑需要在数据上实现的操作开始,需要存取最后一个数据项吗?还是第一个?还是特定值的项?还是特定位置的项?回答这些问题会引出ADT的定义,只有完整的定义了ADT后,才应该考虑实现的细节。
这在我们Java语言中的接口设计理念是想通的。