n个集合的容斥原理
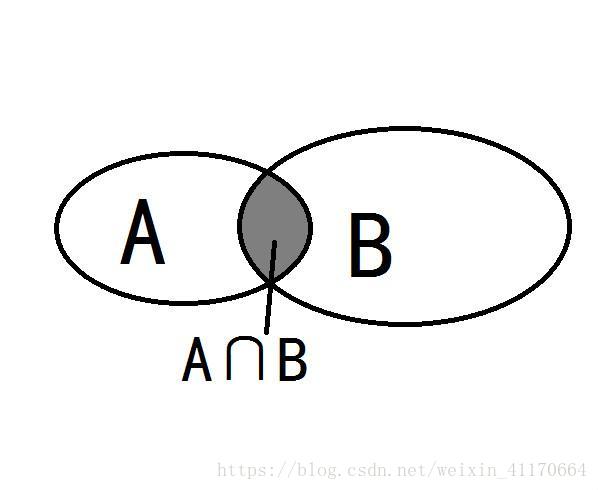
我们知道两个集合的容斥关系
A ∪ B = A + B - A∩B。
三个集合又有怎样的关系呢
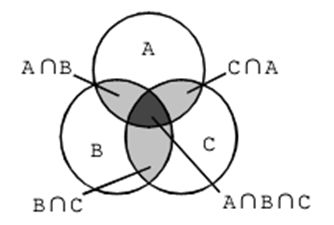
A∪B∪C = A+B+C - (A∩B+A∩C+B∩C) + A∩B∩C
三个集合的容斥原理关系这里不做推导过程可以看图自行推导
从上面的两个例子中不难发现几个集合的并集等于
集合的并集等于 = ①总体先相加→②减去任意两两相交的和→③加上任意三个相交的和。
接下来猜想4个集合的容斥关系是否为
A∪B∪C∪D = A+B+C+D ﹣(A∩B+B∩C+C∩D+A∩C+A∩D+B∩D)+(A∩B∩C+A∩B∩D+B∩C∩D)﹣A∩B∩C∩D呢?
我们没有办法画图验证,我们先用一个实际例子验证一下:
4个集合 A={1,2,3} B={2,3,4} C={1,3,5} D={3,4,5}
根据上面的猜想公式求出 A∪B∪C∪D = {1,2,3,4,5}
结果是正确 但这不能保证对所有4个集合的关系都是正确的。
假设有n个集合 A1,A2,......,An (n≥2)
猜想n个集合的容斥关系是否为:
A1∪A2∪......∪An
= A1 + A2 + ......+ An ﹣(A1∩A2 + A1∩A3 + ......+ A[n-1]∩An) +
(A1∩A2∩A3 + A1∩A2∩A4 + ......+ A[n-2]∩A[n-1]∩An) + ......+
[(-1)^(n-1)]A1∩A2∩......∩An (注:[n-1],[n-2]为下标;(-1)^(n-1)表示-1的n-1次方)
验证推导
为了方便书写先保存一个代数式宏
令M = [ ∑(i=1,k+1)Ai ] ﹣[ ∑(1≤i<j≤k)Ai∩Aj ] + [ ∑(1≤i<j<r≤k)Ai∩Aj∩Ar ] + ......+ (-1)^(k-1) A1∩A2∩......∩An
当n=2时命题显然成立
假设当n=k时命题成立(k≥2)
A1∪A2∪......∪Ak∪A[k+1]
=(A1∪A2∪......∪Ak)∪A[k+1]
=(A1∪A2∪......∪Ak) + A[k+1] - (A[k+1])∩(A1∪A2∪......∪Ak)
=M -{ [(A[k+1]∩A1)∪(A[k+1]∩A2)∪......∪(A[k+1]∩Ak) }
=M - { ∑(i=1,k)Ai∩A[k+1] - ∑(1≤i<j≤k)Ai∩Aj∩A[k+1] + ......+(-1)^(k+1 - 1)A1∩A2∩......∩Ak∩A[k+1] }
=∑(i=1,k+1)Ai - ∑(1≤<j≤k+1)Ai∩Aj + ...... +(-1)^(k+1 - 1)A1∩A2∩......∩A[k+1]
则当n=k+1时命题仍然成立
因此这个结论是正确的
故有当n≥2时的n个集合容斥原理都有如下关系
A1∪A2∪......∪An
= A1 + A2 + ......+ An ﹣(A1∩A2 + A1∩A3 + ......+ A[n-1]∩An) +
(A1∩A2∩A3 + A1∩A2∩A4 + ......+ A[n-2]∩A[n-1]∩An) + ......+
[(-1)^(n-1)]A1∩A2∩......∩An