数据结构(17.1)图之邻接矩阵存储
数据结构(17.1)图之邻接矩阵存储
- 前言
- 图的存储结构
- 邻接矩阵(数组表示法)
- 邻接表
- 十字链表
- 邻接多重表
- 图的初始化
- 顶点和边的插入
- 插入顶点
- 插入边
- 顶点和边的删除
- 删除线
- 删除顶点
- 第一种方法
- 第二种方法
- 全部代码
- Graph.h
- Graph.c
- Main.c
前言
图是一种比线性表和树更复杂的数据结构。
图中的数据元素称为顶点,并且在图中,是不允许没有顶点存在的:图是由顶点的有穷非空集合和顶点之间边的集合组成。
顶点与顶点之间的逻辑关系用边来表示,图中任何的两个顶点都可能存在边,边的集合允许为空。
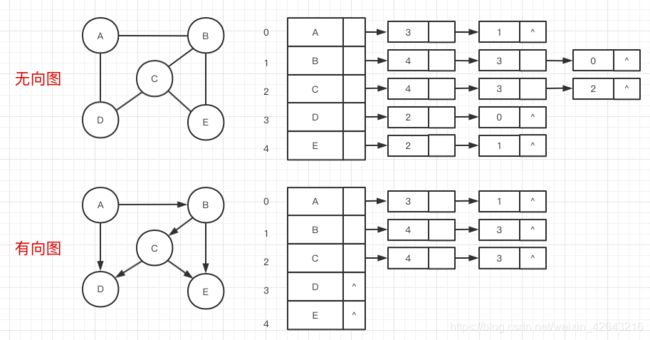
假如顶点与顶点之间的边没有方向,则称其为无向边,用“()”表示;反之则为有向边,用"<>"表示。
当图中所有的边都为无向边时,称该图为无向图;反之为有向图。
我们主要实现的是无向图。
图的存储结构
在之前的数据结构中,都可以有两种不同的存储结构:顺序存储于链式存储。由于图的结构比较复杂,任意两个顶点都可能存在关系,因此无法用数据元素在储存区中的物理位置来表示元素之间的关系。这就说明,用顺序存储结构来存储图很困难,但是可以使用数组来记录顶点与顶点之间的关系。
图的链式存储结构中,由于结点的设计有不同,会有不同的存储结构,常用的有邻接表、十字链表和邻接多重表。
邻接矩阵(数组表示法)
图中顶点与顶点之间的关系(即边的状态)可以通过矩阵来表示:
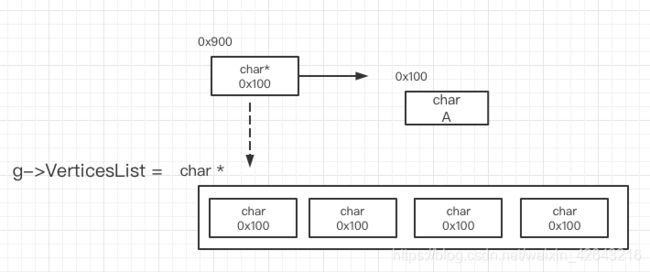
但是,二维数组只能记录边的状态,却没有记录顶点本身。因此在图的结点设计中,还需要一个列表来记录顶点本身。同时,需要记录一下图的最大顶点数量和当前顶点数量、边的数量,结点设计如下:
typedef struct GraphMtx{
//最大的顶点数
int MaxVertices;
//现有的顶点数
int NumVertices;
//现有的边数
int NumEdges;
//顶点列表
char* VerticesList;
//边
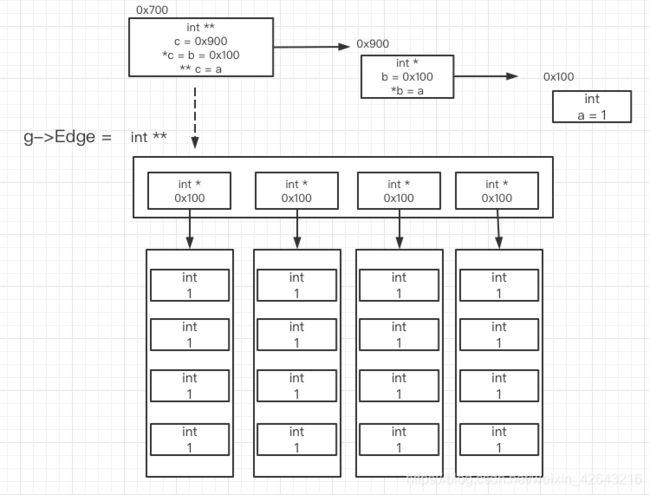
int** Edge;
}GraphMtx;
邻接表
在邻接表存储中,每个顶点的存储类似于一个有头结点的单链表。
首先,设计一个顶点结点,其数据域存储顶点的数据,指针域指向它的边结点列表;这就类似于单链表的头结点。
在边结点中,数据域存储这条边所指向的顶点的位置(在数组中为下标),指针域指向本顶点的下一个边结点;这实际上就是一个单链表。
最后,所有的顶点需要一个列表来存储,多使用一维数组。
因此,我们需要设计三个结构体,分别来表示顶点结点、边结点和图本身。
//边的结构
typedef struct Edge{
//顶点的下标
int dest;
//下一条边
struct Edge* Link;
}Edge;
//顶点的结构
typedef struct Vertex{
//数据域-顶点的信息
char data;
//指针域-指向边
Edge *adj;
}Vertex;
//图
typedef struct GraphLnk{
//最大顶点数量
int MaxVertices;
//当前顶点数量
int NumVertices;
//当前边的数量
int NumEdges;
//顶点的列表
Vertex *NodeTable;
}GraphLnk;
十字链表
十字链表是用于存储有向图的一种链式结构。在有向图中,边分为出边和入边;因此在顶点结点的设计中会有两个指针域,分别指向本顶点的入边列表和出边列表;同样,在边结点中,有两个数据域,分别存储边的头部和尾部的位置(在数组中即下标),也有两个指针域,分别指向本顶点的下一条入边和下一条出边。
//边结点
typedef struct Edge{
//弧尾
int tail;
//弧头
int head;
//下一条入边
int hLink;
//下一条出边
int tLink;
}Edge;
//顶点结点
typedef struct Vertex{
//数据域-顶点的信息
char data;
//入边列表
Edge *EdgeIn;
//出边列表
Edge *EdgeOut;
}Vertex;
//图
typedef struct GraphLnk{
//最大顶点数量
int MaxVertices;
//当前顶点数量
int NumVertices;
//当前边的数量
int NumEdges;
//顶点的列表
Vertex *NodeTable;
}GraphLnk;
邻接多重表
十字链表是用于存储无向图的一种链式结构。观察邻接表可以发现,若使用邻接表来存储无向图,每一条边会生成两个边结点,分别存储到两个顶点的边链表中,这样给边的删除带来麻烦。因此,可以考虑只生成一个边结点,让两个顶点同时指向这条边。这样,边的结点就类似于十字链表的结点,有两个数据域和两个指针域。而顶点结点结构不变。
//边顶点
typedef struct Edge{
//第一个顶点i的位置
int Idest;
//第二个顶点j的位置
int Jdest;
//下一个i顶点的边
struct Edge* ILink;
//下一个j顶点的边
struct Edge* JLink;
}Edge;
//顶点结点
typedef struct Vertex{
//数据域-顶点的信息
char data;
//指针域-指向边
Edge *adj;
}Vertex;
//图
typedef struct GraphLnk{
//最大顶点数量
int MaxVertices;
//当前顶点数量
int NumVertices;
//当前边的数量
int NumEdges;
//顶点的列表
Vertex *NodeTable;
}GraphLnk;
图的初始化
初始化主要包括两个部分:一个是对数据域进行初始化,另一部分是对需要的空间进行开辟。
//初始化
void InitGraph(GraphMtx *g){
//数据初始化
g->MaxVertices = DEFAULT_VERTEX_SIZE;
g->NumVertices = g->NumEdges = 0;
//开辟储存顶点的空间
g->VerticesList = (T*)malloc(sizeof(T) * g->MaxVertices);
assert(g->VerticesList != NULL);
//开辟储存边的空间
g->Edge = (int **)malloc(sizeof(int*) * g->MaxVertices);
assert(g->Edge != NULL);
for (int i = 0; i < g->MaxVertices; i ++) {
g->Edge[i] = (int *)malloc(sizeof(int) * g->MaxVertices);
assert(g->Edge[i] != NULL);
}
//初始化边
for (int i = 0; i < g->MaxVertices; i ++) {
for (int j = 0; j < g->MaxVertices; j ++) {
g->Edge[i][j] = 0;
}
}
}
数据初始化没什么好说的,主要讲一下空间的开辟。这里开辟了两个空间,一个列表用于存放顶点,一个矩阵用于储存边;如图所示,它们实质上是一个一维数组和一个二维数组。
顶点和边的插入
插入线即在两个顶点之间插入一条边,这要求先有顶点,因此需要实现插入顶点的方法。
插入顶点
插入顶点非常简单,已知储存顶点的列表实际上是一个一维数组,直接将数据存入即可。
void InsertVertex(GraphMtx *g,T v){
if (g->NumVertices == g->MaxVertices) {
printf("顶点已满,无法插入\n");
return;
}
g->VerticesList[g->NumVertices ++] = v;
}
插入边
插入边时,由于矩阵本身只表示边,它并不知道哪一行哪一列表示的是哪个顶点,因此我们需要去获取顶点在矩阵中的位置。顶点在矩阵中的位置就是它在顶点列表中的下标,我们写一个方法去获取。
//获取顶点位置
int GetVertexPos(GraphMtx *g,T v){
for (int i = 0; i < g->NumVertices; i ++) {
if (g->VerticesList[i] == v) {
return i;
}
}
return -1;
}
如果顶点不存在,返回的是 -1;当顶点位置为 -1时,也就意味着不用插入了,直接返回。
//插入边
void InsertEdge(GraphMtx *g,T v1,T v2){
//获取v1的位置
int p1 = GetVertexPos(g, v1);
//获取v2的位置
int p2 = GetVertexPos(g, v2);
if (p1 == -1 || p2 == -1) {
printf("有顶点不存在\n");
return;
}
if (g->Edge[p1][p2] != 1) {
//修改数组的值
g->Edge[p1][p2] = g->Edge[p2][p1] = 1;
//修改现有边的数量
g->NumEdges ++;
}
}
如果两个顶点都存在,那么只需要将存储边的二维数组的值修改一下即可。
注:如果是有向边,则只修改对应的坐标值;如果是无向边,则对称的坐标值也需要修改,这里我们实现的是无向图。
顶点和边的删除
在删除中,删除顶点比删除边复杂,因为删除顶点必然要删除与顶点有关的边,因此我们先从删除边说起。
删除线
删除线非常简单,只需要将对应位置的值修改为初始值(0)即可
//删除边
void RemoveEdge(GraphMtx *g,T v1,T v2){
//获取顶点位置
int p1 = GetVertexPos(g, v1);
int p2 = GetVertexPos(g, v2);
if (p1 == -1 || p2 == -1) {
printf("有顶点不存在\n");
return;
}
if (g->Edge[p1][p2] == 1) {
g->Edge[p1][p2] = g->Edge[p2][p1] = 0;
g->NumEdges --;
}
}
删除顶点
删除顶点首先要从顶点列表中删除掉顶点本身,其次要去边的矩阵中删除与顶点有关的边。
至于删除顶点,有两种策略:第一种策略是,该顶点之后的顶点依次前移,这样顶点原本的顺序没有变化;第二种策略是,使用最后一个顶点替换掉本顶点,这样可以减少数据移动的次数。

第一种方法
采用第一种策略,首先获得顶点的位置p,若p不存在,也就不必要删除了。
其次,将顶点删除,即从p顶点开始,直到最后一个顶点,不断用本顶点+1处的数据替换掉原来的数据。
//删除顶点
for (int i = p; i < g->NumVertices-1; i ++) {
g->VerticesList[i] = g->VerticesList[i+1];
}
最后,将边删除。为了思路简单,我们可以先删除行,再删除列,即分别从第p行,第p列开始,用后续的数据替换掉原来的数据。
//删除行
for (int i = p; i < g->NumVertices-1; i ++) {
for (int j = 0; j < g->NumVertices; j++) {
g->Edge[i][j] = g->Edge[i+1][j];
}
}
//删除列
for (int i = p; i < g->NumVertices-1; i ++) {
for (int j = 0; j < g->NumVertices; j ++) {
g->Edge[j][i] = g->Edge[j][i+1];
}
}
最后,需要修改现有顶点和现有边的数量,现有顶点的数量直接减一即可,但是现有边的数量需要在删除之前先统计出来。
//计算要删除的边的数量
int count = 0;
for (int i = 0; i < g->NumVertices; i ++) {
if (g->Edge[p][i] == 1) {
count ++;
}
}
第二种方法
第二种方法步骤上差不多,只是原本需要从p开始向后替换,现在只需要用最后一个顶点的数据来替换p的数据。
//删除顶点->替换
g->VerticesList[p] = g->VerticesList[g->NumVertices-1];
//删除边->替换行
for(int i = 0; i < g->NumVertices; i ++){
g->Edge[p][i] = g->Edge[g->NumVertices-1][i];
}
//替换列
for (int i = 0; i < g->NumVertices; i ++) {
g->Edge[i][p] = g->Edge[i][g->NumVertices-1];
}
全部代码
Graph.h
#ifndef GraphMtx_h
#define GraphMtx_h
#include Graph.c
#include "GraphMtx.h"
//初始化
void InitGraph(GraphMtx *g){
//数据初始化
g->MaxVertices = DEFAULT_VERTEX_SIZE;
g->NumVertices = g->NumEdges = 0;
//开辟储存顶点的空间
g->VerticesList = (T*)malloc(sizeof(T) * g->MaxVertices);
assert(g->VerticesList != NULL);
//开辟储存边的空间
g->Edge = (int **)malloc(sizeof(int*) * g->MaxVertices);
assert(g->Edge != NULL);
for (int i = 0; i < g->MaxVertices; i ++) {
g->Edge[i] = (int *)malloc(sizeof(int) * g->MaxVertices);
assert(g->Edge[i] != NULL);
}
//初始化边
for (int i = 0; i < g->MaxVertices; i ++) {
for (int j = 0; j < g->MaxVertices; j ++) {
g->Edge[i][j] = 0;
}
}
}
//展示图
void ShowGraph(GraphMtx *g){
//打印第一排的顶点
printf(" ");
for (int i = 0; i < g->NumVertices; i ++) {
printf("%c ",g->VerticesList[i]);
}
printf("\n");
//打印边->矩阵
for (int i = 0; i < g->NumVertices; i ++) {
printf("%c ",g->VerticesList[i]);
for (int j = 0; j < g->NumVertices; j ++) {
printf("%d ",g->Edge[i][j]);
}
printf("\n");
}
printf("\n");
}
//获取顶点位置
int GetVertexPos(GraphMtx *g,T v){
for (int i = 0; i < g->NumVertices; i ++) {
if (g->VerticesList[i] == v) {
return i;
}
}
return -1;
}
//插入顶点
void InsertVertex(GraphMtx *g,T v){
if (g->NumVertices == g->MaxVertices) {
printf("顶点已满,无法插入\n");
return;
}
g->VerticesList[g->NumVertices ++] = v;
}
//插入边
void InsertEdge(GraphMtx *g,T v1,T v2){
//获取v1的位置
int p1 = GetVertexPos(g, v1);
//获取v2的位置
int p2 = GetVertexPos(g, v2);
if (p1 == -1 || p2 == -1) {
printf("有顶点不存在\n");
return;
}
if (g->Edge[p1][p2] != 1) {
g->Edge[p1][p2] = g->Edge[p2][p1] = 1;
g->NumEdges ++;
}
}
//删除顶点
void RemoveVertex(GraphMtx *g, T v){
//获取顶点位置
int p = GetVertexPos(g, v);
if (p == -1) {
printf("顶点不存在\n");
return;
}
//删除顶点
for (int i = p; i < g->NumVertices-1; i ++) {
g->VerticesList[i] = g->VerticesList[i+1];
}
//计算要删除的边的数量
int count = 0;
for (int i = 0; i < g->NumVertices; i ++) {
if (g->Edge[p][i] == 1) {
count ++;
}
}
//删除行
for (int i = p; i < g->NumVertices-1; i ++) {
for (int j = 0; j < g->NumVertices; j++) {
g->Edge[i][j] = g->Edge[i+1][j];
}
}
//删除列
for (int i = p; i < g->NumVertices-1; i ++) {
for (int j = 0; j < g->NumVertices; j ++) {
g->Edge[j][i] = g->Edge[j][i+1];
}
}
g->NumVertices --;
g->NumEdges -= count;
}
void RemoveVertex2(GraphMtx *g, T v){
//获取顶点位置
int p = GetVertexPos(g, v);
if (p == -1) {
printf("顶点不存在\n");
return;
}
//删除顶点->替换
g->VerticesList[p] = g->VerticesList[g->NumVertices-1];
//计算要删除的边的数量
int count = 0;
for (int i = 0; i < g->NumVertices; i ++) {
if (g->Edge[p][i] == 1) {
count ++;
}
}
//删除边->替换行
for(int i = 0; i < g->NumVertices; i ++){
g->Edge[p][i] = g->Edge[g->NumVertices-1][i];
}
//替换列
for (int i = 0; i < g->NumVertices; i ++) {
g->Edge[i][p] = g->Edge[i][g->NumVertices-1];
}
g->NumVertices --;
g->NumEdges -= count;
}
//删除边
void RemoveEdge(GraphMtx *g,T v1,T v2){
//获取顶点位置
int p1 = GetVertexPos(g, v1);
int p2 = GetVertexPos(g, v2);
if (p1 == -1 || p2 == -1) {
printf("有顶点不存在\n");
return;
}
if (g->Edge[p1][p2] == 1) {
g->Edge[p1][p2] = g->Edge[p2][p1] = 0;
g->NumEdges --;
}
}
//获取第一个邻接顶点
int GetFirstNeighbor(GraphMtx *g,T v){
int p = GetVertexPos(g, v);
if (p == -1) {
return -1;
}
for (int i = 0; i < g->NumVertices; i ++) {
if (g->Edge[p][i] == 1) {
return i;
}
}
return -1;
}
//获取顶点v的邻接顶点w的下一个邻接顶点
int GetNextNeighbor(GraphMtx *g,T v,T w){
int pv = GetVertexPos(g, v);
int pw = GetVertexPos(g, w);
if (pv == -1 || pw == -1) {
return -1;
}
for (int i = pw+1; i < g->NumVertices; i ++) {
if (g->Edge[pv][i] == 1) {
return i;
}
}
return -1;
}
//摧毁图
void DestoryGraph(GraphMtx *g){
//释放顶点空间
free(g->VerticesList);
g->VerticesList = NULL;
for (int i = 0; i < g->NumVertices; i ++) {
free(g->Edge[i]);
}
g->Edge = NULL;
g->MaxVertices = g->NumEdges = g->NumVertices = 0;
}
Main.c
#include "GraphMtx.h"
int main(int argc, const char * argv[]) {
GraphMtx gm;
InitGraph(&gm);
InsertVertex(&gm, 'A');
InsertVertex(&gm, 'B');
InsertVertex(&gm, 'C');
InsertVertex(&gm, 'D');
InsertVertex(&gm, 'E');
InsertEdge(&gm, 'A', 'B');
InsertEdge(&gm, 'A', 'D');
InsertEdge(&gm, 'B', 'C');
InsertEdge(&gm, 'B', 'E');
InsertEdge(&gm, 'C', 'E');
InsertEdge(&gm, 'C', 'D');
ShowGraph(&gm);
int p = GetFirstNeighbor(&gm, 'A');
printf("%d\n",p);
p = GetNextNeighbor(&gm, 'A', 'B');
printf("%d\n",p);
//删除边
// RemoveEdge(&gm, 'B', 'C');
// ShowGraph(&gm);
//删除顶点
RemoveVertex(&gm, 'C');
ShowGraph(&gm);
DestoryGraph(&gm);
return 0;
}