数据结构（18）图的遍历

前言

图的遍历与树类似，都是从某一顶点出发访问其余顶点，并且使每一个顶点只被访问一次。但是，树只能从根结点出发，图却能从任意顶点出发，并且图中的任意顶点都可能与其他顶点相连接，这就使图的遍历比树复杂得多。

图有连通图与非连通图之分。所谓连通图，即图中的任意两个顶点都存在路径；反之则为非连通图。连通图与非连通图在遍历时会遇上不同的情况。我们重点说的是连通图的遍历。

连通图

根据遍历策略的不同，图的遍历有两种方法：深度优先遍历和广度优先遍历。

深度优先遍历

深度优先遍历类似于树的先序遍历：从某个顶点A出发，先访问本结点A，再访问A的一个未访问过的邻接顶点B；接着从B顶点出发，访问B的一个未访问过的邻接顶点C；再从C出发，访问C的一个邻接顶点D……当D无邻接顶点时，返回到C，再去访问C的下一个邻接顶点E，以此类推，等C的邻接顶点访问完毕后，会返回到B，再去找B的下一个邻接顶点，直到整个图遍历结束为止。

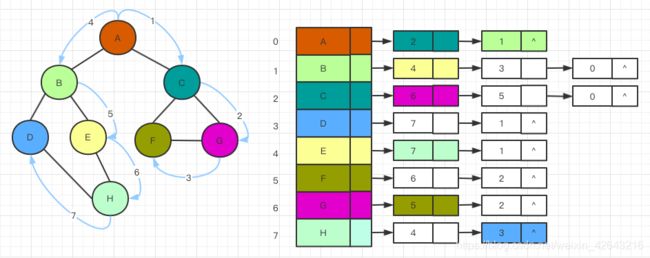
既然类似于树的先序遍历，那么很明显可以用递归来实现，以上图为例分析一下递归的过程：

• 从A出发，访问A，获取到A的一个未访问过的邻接顶点C，递归调用遍历方法
• 从C出发，访问C，获取到C的一个未访问过的邻接顶点G，递归调用遍历方法
• 从G出发，访问G，获取到G的一个未访问过的邻接顶点F，递归调用遍历方法
• 从F出发，访问F，F的邻接顶点G、C都被访问过了，返回上一层递归
• 此时在G顶点的递归，找到G的下一个邻接顶点C，也被访问过了，返回上一层递归
• 此时在C顶点的递归，C的下一个邻接顶点F、A都被访问过了，返回上一层递归
• 此时在A顶点的递归，找到A的下一个未访问过的邻接顶点B，递归调用遍历方法
• 从B出发，访问B，找到B的一个未访问过的邻接顶点E，递归调用遍历方法
• 从E出发，访问E，找到E的一个未访问过的邻接顶点H，递归调用遍历方法
• 从H出发，访问H，找到H的一个未访问过的邻接顶点D，递归调用遍历方法
• 从D出发，访问D，D的邻接顶点H、B都被访问过了，返回上一层递归
• 此时在H顶点的递归，H已经没有下一个邻接顶点了，返回上一层递归
• 此时在E顶点的递归，E的下一个邻接顶点B已经被访问过了，返回上一层递归
• 此时在B顶点的递归，B的下一个邻接顶点D、A都被访问过了，返回上一层递归
• 此时在A顶点的递归，A已经没有下一个邻接顶点了，递归调用结束

那么，如何实现这个算法呢？

由于图的访问可以从任何一个顶点开始，因此需要用户传入一个起始顶点。然后从本顶点起，依次去访问本顶点未曾访问过的邻接顶点。

为了记录每个顶点是否被访问过，要额外设一个辅助数组visited记录顶点的访问状态。

void DFS(GraphLnk *g,int v,int *visited){
    //访问本顶点
    printf("%2c",GetVertexValue(g, v));
    //修改标记
    visited[v] = 1;
    
    //获取第一个邻接顶点
    int w = GetFirstNeighbor(g, GetVertexValue(g, v));
    while (w != -1) {
        //判断该邻接顶点是否访问过
        if (!visited[w]) {
            //未访问过 ->递归调用遍历方法
            DFS(g, w, visited);
        }
        //获取下一个邻接顶点
        w = GetNextNeighbor(g, GetVertexValue(g, v), GetVertexValue(g, w));
    }
}

上面的代码里提到了两个方法：获取第一个邻接顶点和下一个邻接顶点。

首先，我们采用的是邻接表的存储方式，也就是说存储边的是一个链表，并且链表中存放的是邻接顶点的地址。

那么获取第一个邻接顶点就很简单：找到要查找的邻接顶点，然后返回链表中的第一个结点即可。

//获取第一个邻接顶点
int GetFirstNeighbor(GraphLnk *g,T vertex){
    //得到顶点的位置
    int v = GetVertexPos(g, vertex);
    if (v == -1) {
        return -1;
    }
    //获取边链表的第一个结点
    Edge *p = g->NodeTable[v].adj;
    //如果结点存在，返回邻接顶点所在的下标
    return p == NULL ? -1 : p->dest;
}

获取下一个邻接顶点指的是，获取v1顶点的，处于v2顶点之后的那个邻接顶点。也就是说需要遍历v1顶点的边链表，找到v2顶点的位置，然后返回v2之后的那个顶点（如果存在）

//获取下一个邻接顶点
int GetNextNeighbor(GraphLnk *g,T vertex1,T vertex2){
    int v1 = GetVertexPos(g, vertex1);
    int v2 = GetVertexPos(g, vertex2);
    if (v1 == -1 || v2 == -1) {
        return -1;
    }
    
    Edge *p = g->NodeTable[v1].adj;
    //找到v2顶点的位置
    while (p != NULL && p->dest != v2) {
        p = p->Link;
    }
    //返回v2顶点的下一个顶点（非空）
    if (p != NULL && p->Link != NULL) {
        return p->Link->dest;
    }
    return -1;
}

广度优先遍历

广度优先遍历类似于树的层次遍历：从某个顶点A出发，先访问本结点A，再访问A的所有未访问过的邻接顶点C、D、E，访问C的所有未访问过的邻接顶点E、F；D的所有未访问过的邻接顶点，E的所有未访问过的邻接顶点…以此类推。

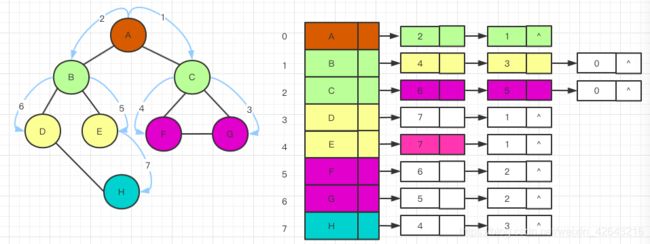
既然类似于层次遍历，就需要用队列来实现，以上图为例分析：

• A结点入队
• 此时队首元素为A，获取队首元素A并出队，A未被访问过，则访问A，A的所有未访问过的邻接顶点C、B入队
• 此时队首元素为C，获取队首元素C并出队，C未被访问过，则访问C，C的所有未访问过的邻接顶点G、F入队
• 此时队首元素为B，获取队首元素B并出队，B未被访问过，则访问B，B的所有未访问过的邻接顶点E、D入队
• 此时队首元素为G，获取队首元素G并出队，G未被访问过，则访问G，G的所有未访问过的邻接顶点F入队
• 此时队首元素为F，获取队首元素F并出队，F未被访问过，则访问F，F的邻接顶点均被访问过，无入队
• 此时队首元素为E，获取队首元素E并出队，E未被访问过，则访问E，E的所有未访问过的邻接顶点H入队
• 此时队首元素为D，获取队首元素D并出队，D未被访问过，则访问D，D的所有未访问过的邻接顶点H入队
• 此时队首元素为F，获取队首元素F并出队，F已访问过，无操作
• 此时队首元素为H，获取队首元素H并出队，H未被访问过，则访问H，H的邻接顶点均被访问过,无入队
• 此时队首元素为H，获取队首元素H并出队，H已访问过，无操作
• 队列已空，遍历结束

同样，广度优先遍历中也需要一个辅助数组来标记结点的访问情况，这里的队列用到了我们之前实现的队列结构

void BFS(GraphLnk *g,int v,int *visited){
    //创建队列
      LinkQueue Q;
      InitQueue(&Q);
      
      //第一个结点入队
      EnQueue(&Q, v);
      
      while (!Empty(&Q)) {
          //获取队首元素
          GetHead(&Q, &v);
          //队首元素出队
          DeQueue(&Q);
          //访问
          if (!visited[v]) {
              printf("%2c",GetVertexValue(g, v));
              visited[v] = 1;
              
              //队首的邻接顶点入队
              int w = GetFirstNeighbor(g, GetVertexValue(g, v));
              
              while (w != -1) {
                  if (visited[w] != 1) {
                      EnQueue(&Q, w);
                  }
                  w = GetNextNeighbor(g, GetVertexValue(g, v), GetVertexValue(g, w));
              }
              
          }
          
      }
}

非连通图

非连通图的问题在于，有顶点之间是不存在路径的。

假设用我们的方法来遍历，从A顶点出发，只能得到A-B-M-L-C-F的序列，D-E和G-H-I-K都是访问不到的。

要解决这个问题，课本中提到了生成树的方法，但比较复杂。我们这里用了一个很简单的思路：遍历顶点列表中的每一个顶点，若它没有访问过，则调用之前写好的深度优先或广度优先搜索方法进行遍历。这样就一定可以使每一个顶点出发的连通分量被遍历到。

//遍历-非联通图
void Components(GraphLnk *g){
    int n = g->NumVertices;
    //辅助空间 1-访问过 0-未访问
    int *visited = (int *)malloc(sizeof(int) * n);
    assert(visited != NULL);
    //初始化辅助空间
    for (int i = 0; i < n; i ++) {
        visited[i] = 0;
    }
    
    for (int i = 0; i < n; i ++) {
        if (!visited[i]) {
            BFS(g, i, visited);
        }
    }
    free(visited);
}

全部代码

这篇的代码比较复杂，就用网盘分享吧。

图的遍历-微云