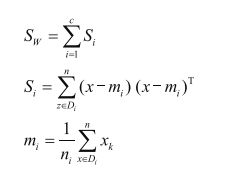python--LDA线性判别分析模型
以下内容笔记出自‘跟着迪哥学python数据分析与机器学习实战’,外加个人整理添加,仅供个人复习使用。
导入数据
import numpy as np
import pandas as pd
df=pd.read_csv(r'iris.data')
print(df.shape)
#查看类别
print(set(df['Iris-setosa']))
df.columns=['sepal length','sepal width',
'petal length','petal width','class label']
df.head(6)
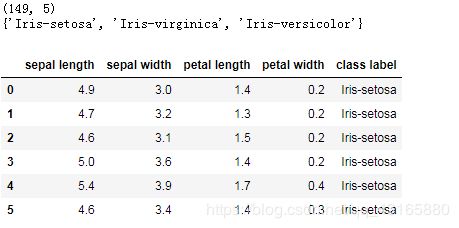
由于标签是分类型数据,需要转换一下。
现在需要将四维数据特征降维。
from sklearn.preprocessing import LabelEncoder
X=df[['sepal length','sepal width',
'petal length','petal width']].values
y=df['class label'].values
#映射标签(使用sklearn包快速完成标签转换)
enc=LabelEncoder()
y=enc.fit_transform(y)+1
print(set(y))
{1, 2, 3}
不使用sklearn调包
求解类内散布矩阵
import numpy as np
np.set_printoptions(precision=4)
#保存均值
mean_vectors=[]
#计算类别
for cl in range(1,4):
mean_vectors.append(np.mean(X[y==cl],axis=0))
print('均值类别%s:%s\n' % (cl,mean_vectors[cl-1]))
均值类别1:[5.0041 3.4163 1.4653 0.2449]
均值类别2:[5.936 2.77 4.26 1.326]
均值类别3:[6.588 2.974 5.552 2.026]
注意这里是四个特征,上面的输出是3个类别,每个类别分别的特征均值,4维向量。
计算类内散布矩阵
s_w=np.zeros((4,4)) #4个特征
for cl,mv in zip(range(1,4),mean_vectors):
class_sc_mat=np.zeros((4,4))
for row in X[y==cl]:
#对每个特征进行计算
row,mv=row.reshape(4,1),mv.reshape(4,1)
#上面的计算公式
class_sc_mat+=(row-mv).dot((row-mv).T)
s_w+=class_sc_mat
print('类内散布矩阵:\n',s_w)
类内散布矩阵:
[[38.9472 13.6751 24.6201 5.6598]
[13.6751 17.0281 8.1254 4.9169]
[24.6201 8.1254 27.2158 6.2507]
[ 5.6598 4.9169 6.2507 6.1736]]
计算类间散布矩阵
#全局均值
overall_mean=np.mean(X,axis=0)
overall_mean
array([5.8483, 3.051 , 3.7745, 1.2054])
#类间散布矩阵
s_b=np.zeros((4,4))
#对各类别分别计算
for i,mean_vec in enumerate(mean_vectors):
#当前类别样本数
n=X[y==i+1,:].shape[0]
mean_vec=mean_vec.reshape(4,1)
overall_mean=overall_mean.reshape(4,1)
#上述公式
s_b+=n*(mean_vec-overall_mean).dot((mean_vec-overall_mean).T)
print('类间散布矩阵:\n',s_b)
类间散布矩阵:
[[ 62.6649 -19.1924 163.3935 70.6115]
[-19.1924 10.7842 -55.0015 -22.0477]
[163.3935 -55.0015 431.0473 184.5397]
[ 70.6115 -22.0477 184.5397 79.6021]]
组合类内与类间矩阵
#求解特征值、特征向量
eig_vals,eig_vecs=np.linalg.eig(np.linalg.inv(s_w).dot(s_b)) #s_w求解逆矩阵
for i in range(len(eig_vals)):
eigvec_sc=eig_vecs[:,i].reshape(4,1)
print('\n特征向量{}:\n{}'.format(i+1,eigvec_sc.real))
print('特征值{:}: {:.2e}'.format(i+1,eig_vals[i].real))

结果得到4个特征向量和其对应的特征值。特征向量直接观察较麻烦,因为投影在高维上较难理解,特征值较直观。这里可以认为特征值代表的是其所对应特征向量的重要程度,特征值越大,所对应的特征向量越重要,所以接下来可进行排序。
#特征值和特征向量配对
eig_pairs=[(np.abs(eig_vals[i]),eig_vecs[:,i]) for i in range(len(eig_vals))]
#排序
eig_pairs=sorted(eig_pairs,key=lambda k:k[0],reverse=True)
print('特征排序结果:\n')
for i in eig_pairs:
print(i[0])
特征排序结果:
31.874579396957305
0.27693748627003545
3.6168880269018654e-15
3.6168880269018654e-15
print('特征值占总体百分比:\n')
eigv_sum=sum(eig_vals)
for i,j in enumerate(eig_pairs):
print('特征值[0:]: {1:.2%}'.format(i+1,(j[0]/eigv_sum).real))
特征值占总体百分比:
特征值[0:]: 99.14%
特征值[0:]: 0.86%
特征值[0:]: 0.00%
特征值[0:]: 0.00%
可以看出,第一个特征值占总体99.14%,第二个只占0.86%,第三个和第四个微不足道,这表示降维时,可以降到二维或一维,没有必要降到三维。
最终选择降到2维
W=np.hstack((eig_pairs[0][1].reshape(4,1),
eig_pairs[1][1].reshape(4,1)))
print('矩阵W:\n',W.real)
矩阵W:
[[-0.2051 -0.0084]
[-0.3869 -0.5891]
[ 0.5463 0.2545]
[ 0.714 -0.7669]]
#执行降维
X_lda=X.dot(W)
print(X_lda.shape)
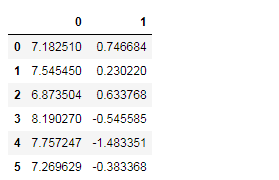
pd.DataFrame(X_lda).head(6)
作图比较
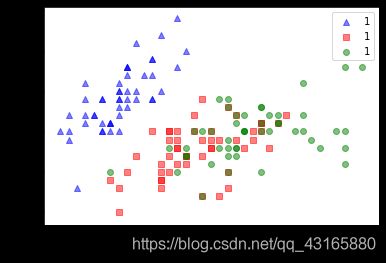
原始数据中挑两个特征作图:
import matplotlib.pyplot as plt
def plot_lda():
ax=plt.subplot(111)
for label,marker,color in zip(
range(1,4),('^','s','o'),('blue','red','green')):
plt.scatter(x=X[:,0].real[y==label],
y=X[:,1].real[y==label],
marker=marker,
color=color,
alpha=0.5,
label=y[label])
plt.xlabel('X[0]')
plt.ylabel('X[1]')
#plt.legend()
plot_lda()
def plot_lda():
ax=plt.subplot(111)
for label,marker,color in zip(
range(1,4),('^','s','o'),('blue','red','green')):
plt.scatter(x=X_lda[:,0].real[y==label],
y=X_lda[:,1].real[y==label],
marker=marker,
color=color,
alpha=0.5,
label=y[label])
plt.xlabel('X[0]')
plt.ylabel('X[1]')
#plt.legend()
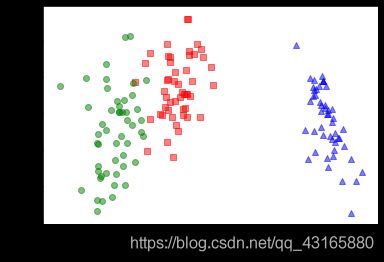
plot_lda()

可以看到,如果对原始数据集随机取两维数据,数据集并不能按类别划分开,但降维后的数据点,区分的较为明显。
(当拿到一份规模较大的数据集时,如何选定维数呢?一方面可以通过观察特征值排序结果实现,另一方面还可以通过实验来进行交叉验证)
sklearn调包
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
sklearn_LDA=LDA(n_components=2)
X_lda_sklearn=sklearn_LDA.fit_transform(X,y)
pd.DataFrame(X_lda_sklearn).head(6)
def plot_lda():
ax=plt.subplot(111)
for label,marker,color in zip(
range(1,4),('^','s','o'),('blue','red','green')):
plt.scatter(x=X_lda_sklearn[:,0].real[y==label],
y=X_lda_sklearn[:,1].real[y==label],
marker=marker,
color=color,
alpha=0.5,
label=y[label])
plt.xlabel('X[0]')
plt.ylabel('X[1]')
#plt.legend()
plot_lda()