基于关联规则的推荐算法详解(Apriori 、FP−Growth)
关联规则分析也是一种比较常见的推荐算法,主要是根据历史数据统计不同规则出现的关系,比如:X−>Y X->YX−>Y,表示X XX事件发生后,Y YY事件也会有一定概率发生。
关联规则分析最著名的就是“啤酒-尿布”的经典案例,沃尔玛的超市管理人员通过数据发现,很多买尿布的人大概率事件会去购买啤酒。这是因为在美国很多妈妈在家带孩子,所以去超市买尿布的任务就交给了爸爸,而一般爸爸都会在买尿布的时候顺手买一罐啤酒喝,所以明明是不相关的两个东西就有了很大的关联。
关联规则分析的最终目标就是要找出强关联规则。一般使用Apriori 、FP−Growth、 Eclat算法。这里我们主要分析一下Apriori 。
Apriori算法
Apriori算法是生成频繁集的一种算法。Apriori原理有个重要假设,如果某个项集是频繁的,那么它的所有子集势必也是频繁的。如果一个项集是非频繁项集,那么它所对应的超集就全都是非频繁项集。传统的Apriori算法的计算量很大,当商品数据量大时基本上效率很低,所以后来有FP-Tree算法优化了该算法。
在电商平台中,常用的关联规则应用是单品推荐单品,即一般只需要知道频繁2项集即可。而且商品并不是全部平等销售的,组合、搭售、买赠、企业采购等订单都会影响频繁集的生成,若仅用支持度衡量物品之间的关联性,很容易导致出现假性关联。
在关联规则中,因为支持度表示在历史中A和B同时购买的概率,置信度表示A推荐B的可信程度。由此可以采用提升度=支持度(Support)*置信度(Confidence )的方式来表示A推荐B而A和B同时购买的概率。这样相比于单纯使用支持度更全面,同时避免了支持度中等或置信度中等的关联规则被淘汰。

- 实例分析
假设用户会同时购买多个手机,我们就不管手机用途了,送人也好,买了摔也行,我们搜集了下面四个用户的购买记录:

假设我们的最小支持度为0.5,最小置信度为0.75。首先计算最少个数项集的支持度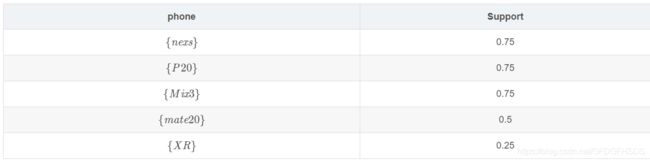
因为最小支持度为0.5,所以 {XR} 不符合,直接被剔除。将项集个数增加一位,如果拓展项集有子集{XR} ,直接去掉。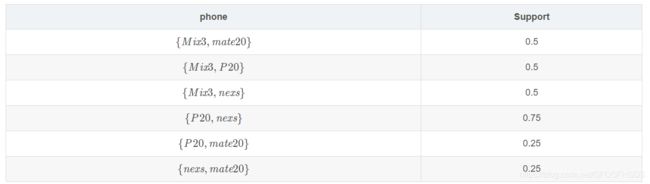

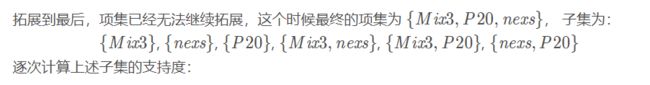


置信度
表示了这条规则有多大程度上值得可信。设条件的项的集合为A,结果的集合为B。置信度计算在A中,同时也含有B的概率。即Confidence(A==>B)=P(B|A)。例 如计算"如果Orange则Coke"的置信度。
支持度
计算在所有的交易集中,既有A又有B的概率。
计算每个规则的支持度,置信度,提升度。首先作变量声明:
f->i 表示具备特征f的用户购买商品i的事件
sf,i 表示规则f->i的支持度
cf,i 表示规则f->i的置信度
sf,i 计算方法为:统计表3中同时满足特征=f,商品=i,用户是否购买=0的记录条数记为
规则选择,规则可以通过以下条件进行过滤。
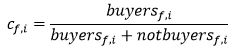
条件1:大于等于某个值,参考值取20-100。
条件2:对所有规则的支持度做降序,取75位数为参考值,sf,i>=这个值。
条件3:对所有规则的置信度做降序,取75位数为参考值,cf,i>=这个值。
Step4:给用户推荐商品
给定一个用户u和一个商品i,通过上述方法生成用户u的特征集合记为F. 我们用该用户特征集合下,所有对i有效特征的均值衡量用户u对该物品的购买可能性p(u,i):
![]()
通过上述公式对全库商品求top 10得分的商品推荐给用户。在实际计算当中,并非会进行全库计算,而是采用特征索引技术进行减少大量冗余计算。
代码
import sys
from itertools import chain, combinations
from collections import defaultdict
from optparse import OptionParser
def subsets(arr):
""" Returns non empty subsets of arr"""
return chain(*[combinations(arr, i + 1) for i, a in enumerate(arr)])
def returnItemsWithMinSupport(itemSet, transactionList, minSupport, freqSet):
"""calculates the support for items in the itemSet and returns a subset
of the itemSet each of whose elements satisfies the minimum support"""
_itemSet = set()
localSet = defaultdict(int)
for item in itemSet:
for transaction in transactionList:
if item.issubset(transaction):
freqSet[item] += 1
localSet[item] += 1
for item, count in localSet.items():
support = float(count)/len(transactionList)
if support >= minSupport:
_itemSet.add(item)
return _itemSet
def joinSet(itemSet, length):
"""Join a set with itself and returns the n-element itemsets"""
return set([i.union(j) for i in itemSet for j in itemSet if len(i.union(j)) == length])
def getItemSetTransactionList(data_iterator):
transactionList = list()
itemSet = set()
for record in data_iterator:
transaction = frozenset(record)
transactionList.append(transaction)
for item in transaction:
itemSet.add(frozenset([item])) # Generate 1-itemSets
return itemSet, transactionList
def runApriori(data_iter, minSupport, minConfidence):
"""
run the apriori algorithm. data_iter is a record iterator
Return both:
- items (tuple, support)
- rules ((pretuple, posttuple), confidence)
"""
itemSet, transactionList = getItemSetTransactionList(data_iter)
freqSet = defaultdict(int)
largeSet = dict()
# Global dictionary which stores (key=n-itemSets,value=support)
# which satisfy minSupport
assocRules = dict()
# Dictionary which stores Association Rules
oneCSet = returnItemsWithMinSupport(itemSet,
transactionList,
minSupport,
freqSet)
currentLSet = oneCSet
k = 2
while(currentLSet != set([])):
largeSet[k-1] = currentLSet
currentLSet = joinSet(currentLSet, k)
currentCSet = returnItemsWithMinSupport(currentLSet,
transactionList,
minSupport,
freqSet)
currentLSet = currentCSet
k = k + 1
def getSupport(item):
"""local function which Returns the support of an item"""
return float(freqSet[item])/len(transactionList)
toRetItems = []
for key, value in largeSet.items():
toRetItems.extend([(tuple(item), getSupport(item))
for item in value])
toRetRules = []
for key, value in largeSet.items()[1:]:
for item in value:
_subsets = map(frozenset, [x for x in subsets(item)])
for element in _subsets:
remain = item.difference(element)
if len(remain) > 0:
confidence = getSupport(item)/getSupport(element)
if confidence >= minConfidence:
toRetRules.append(((tuple(element), tuple(remain)),
confidence))
return toRetItems, toRetRules
def printResults(items, rules):
"""prints the generated itemsets sorted by support and the confidence rules sorted by confidence"""
for item, support in sorted(items, key=lambda (item, support): support):
print "item: %s , %.3f" % (str(item), support)
print "\n------------------------ RULES:"
for rule, confidence in sorted(rules, key=lambda (rule, confidence): confidence):
pre, post = rule
print "Rule: %s ==> %s , %.3f" % (str(pre), str(post), confidence)
def dataFromFile(fname):
"""Function which reads from the file and yields a generator"""
file_iter = open(fname, 'rU')
for line in file_iter:
line = line.strip().rstrip(',') # Remove trailing comma
record = frozenset(line.split(','))
yield record
if __name__ == "__main__":
optparser = OptionParser()
optparser.add_option('-f', '--inputFile',
dest='input',
help='filename containing csv',
default=None)
optparser.add_option('-s', '--minSupport',
dest='minS',
help='minimum support value',
default=0.15,
type='float')
optparser.add_option('-c', '--minConfidence',
dest='minC',
help='minimum confidence value',
default=0.6,
type='float')
(options, args) = optparser.parse_args()
inFile = None
if options.input is None:
inFile = sys.stdin
elif options.input is not None:
inFile = dataFromFile(options.input)
else:
print 'No dataset filename specified, system with exit\n'
sys.exit('System will exit')
minSupport = options.minS
minConfidence = options.minC
items, rules = runApriori(inFile, minSupport, minConfidence)
printResults(items, rules)
基于FP-Tree的关联规则FP-Growth推荐算法
挖掘关联规则的过程中,无可避免要处理海量的数据,也就是事务数据库如此之大,如果采用Apriori算法来挖掘,每次生成频繁k-项集的时候,可能都需要扫描事务数据库一遍,这是非常耗时的操作。那么,可以想尽办法来减少扫描事务数据库的次数,来改进挖掘频繁关联规则的效率。
FP-tree是频繁模式树,它是将整个事务数据库压缩到一棵频繁模式树上。而且,在构造整个事务数据库的的FP-tree的过程中,只需要扫描一次事务数据库就能生成。比AproriGen算法生成候选频繁项集要节省很多时间。
构造FP-tree思想
为了方便遍历FP-tree,设置了一个头表,该头结点结构由2个域组成:
itemName:频繁1-项集名称(以项集作为标识),也就是FP-tree中具有相同nodeName的节点使用nodeLink链接起来以后形成一个链表,该链表的头即为itemName(可以考虑使用LinkedHashMap类型的头表,键为项目名称,值为具有相同itemName第一个FPTNode结点,该结点也是所有具有相同itemName的结点的链表的头);
nodeHead:头表中itemName对应的链表的头指针,也就是,FP-tree中具有相同nodeName节点使用nodeLink链接起来以后形成的一个链表的头,nodeHead指针就指向这个链表的第一个FP-tree结点。
另外,对于FP-tree的根结点,为了方便测试,可以考虑按照如下方式设置:
设置一个集合root,用来存放已经处理过的事务对应的项集的第一个项目,root集合中项目元素不重复。
每次处理一条事务的时候,首先需要判断项集中第一个项目对应的FPTnode,是否与根结点的直接孩子结点(判断nodeName相同即可),如果相同,就说明该项目构造的FPTNode已经在FP-tree中,共享存在的那个结点,无需再创建,只需要修改统计计数(加1);如果不同,就需要构造一个新的结点,作为根结点的直接孩子结点,同时需要在root中登记该新节点的nodeName,并加入到头表中具有nodeName的链表的末尾。
从FP-tree的根结点出发,它的直接孩子结点是事务数据库中一个事务对应的项集,经过对其中的项目排序后得到第一个项目构成的频繁1-项集,由这个频繁1-项集构成根结点的直接孩子结点。
关联规则挖掘FP-growth算法,是通过遍历上面构造的整个事务数据库的频繁模式树来生成频繁项集。
FP-growth算法基本思想描述如下:
第一步:构造整个事务数据库的FP-tree
关于FP-tree的构造可以参考前面的文章 FP- tree的数据结构及其构造 。这里假设已经能够构造出FP-tree,接着就是在整个事务数据库对应的FP-tree的基础上挖掘频繁项集。在下面的步骤中,需要对FP-tree的结构及其内容熟悉。
第二步:挖掘条件模式基
在构造的整个事务数据库的频繁模式树上进行条件模式基的挖掘。
条件模式基,就是选定一个基于支持计数降序排序的频繁1-项集项目,假设为Item,也就是FP-tree的头表中的频繁1-项集项目(已经知道,头表中频繁1-项集项目是按照降序排列的),此时,称该频繁1-项集项目Item为后缀。
纵向沿着头表向上,也就是按照头表中频繁1-项集支持计数的升序方向,优先遍历头表;在遍历头表的过程中同时横向遍历每个频繁1-项集对应的链表域。
通过横向遍历该频繁1-项集项目Item对应的链表域——每个链表中的FPTNode结点都具有一个直接父亲结点的nodeParent指针,纵向向上遍历直到根结点停止,就得到了一个序列(不包含Item对应的横向链表中的结点),这个序列就是条件模式基。
在遍历的过程中,每个条件模式序列中每个FPTNode结点肯定出现一次;以Item频繁1-项集项目横向遍历得到的序列,都是以Item为后缀的。
最后,整棵FP-tree遍历完毕,得到全部的条件模式基。
第三步:根据条件模式基建立局部FP-tree
对上面得到的条件模式基,对每个头表中的频繁1-项集对应的条件模式,作为数据输入源来构造局部FP-tree,也就是条件模式基的FP- tree。因为每个条件模式基的数据量与整个事务数据库相比,显得非常小,建树不会消耗太多时间;而全部的条件模式基就相当于整个事务数据库,所以大约需要扫描两次事务数据库。
建立条件模式基的局部FP-tree,分为单个分支和多个分支两种情况,大体过程是这样的:
(1)对于单个分支:
扫描每个条件模式基,统计在每个单个分支中FPTNode结点中1-项集的支持计数,如果一个头表中的项目Item对应的条件模式基扫描完成,最终的计数不能满足最小支持计数,需要将该结点删除掉,因为它与其他结点组合以后,每个含有该结点的项集一定不满足最小支持计数。
根据上面得到的满足最小支持计数的序列来构造局部FP-tree,因为得到的FPtree是单个分支的,遍历该FP-tree能够得到一个Item 的全部满足最小支持计数的序列,从而将该序列中的全部项目进行组合计算,得到全部组合序列,对于每个序列都将当前头表中Item加入到其中,就得到了包含 Item的全部频繁项集。
(2)对于多个分支:
如果存在分支的,需要递归挖掘频繁项集。因为对于多个分支,递归到出口一定是对应着单个分支的,可以类似上一种情况,处理单个分支,得到频繁项集。
第四步:挖掘频繁关联规则
在上面的步骤中,已经得到了全部的频繁项集,这时挖掘频繁关联规则与Apriori算法的频繁关联规则挖掘的步骤相同。
通过上面的步骤,就完成了频繁关联规则的挖掘。我认为,该算法的思想还是非常清晰的。在基于FP-tree的关联规则挖掘FP-growth算法中,构造整个事务数据库的FP-tree是一个难点,需要保证在构造的过程中不丢失数据结点;另一个难点就是在处理得到的条件模式基的时候,对于具有多个分支的情况,采用递归的思想挖掘,保证不漏掉任何频繁项集。