人工智能AI与物理学（二）（A Topical Review There is no royal road to unsupervised learning）
Physicist’s Journeys Through the AI World - A Topical Review There is no royal road to unsupervised learning
- 摘要（Abstract）
- Ⅳ SCINET：物理机器（SCINET: A PHYSICS MACHINE）
- A.实验一：阻尼摆实验（Experiment One: Damped Pendulum）
- B.实验二：量子位预测（B. Experiment Two: Qubits）
- C.实验三：日心说模型（ Experiment Three: Heliocentric Model）
- Ⅴ AI物理学家（THE AI PHYSICIST）
- A.框架（ Architecture）
- B.学习算法（B. The Learning Algorithm）
- 1.提出理论（ Proposing theories）
- 2.分而治之算法（ Divide-and-conquer algorithm）
- 3.添加理论（Adding theories）
- 4.奥卡姆剃刀原理（Occam’s razor）
- 5.统一算法（Unification algorithm）
- C.总结获得的知识（Summing up Acquired Knowledge）
- 1.消除过度领域（1. Eliminating transition domains）
- Ⅵ 结论（ CONCLUSION）
- A.结束语（Concluding Remarks）
- B.展望（ Outlook）
- 附录
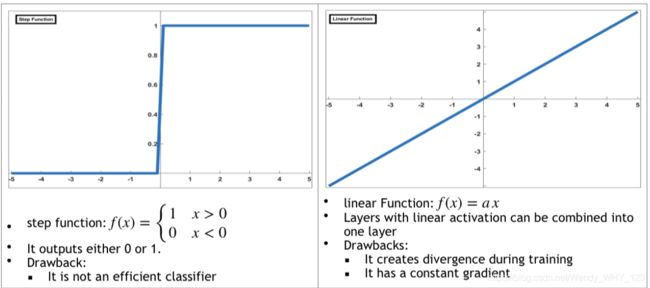
- A.激活函数（Activation Functions）
- B.K-均值聚类（ K-means Clustering）
原文作者：Imad Alhousseini,Wissam Chemissany,Fatima Kleit,Aly Nasrallah
翻译者：Wendy
摘要（Abstract）
以最简单的形式定义人工智能（AI），是使机器变得智能的一种技术工具。由于智能的核心是学习，因此机器学习是人工智能的核心子领域。深度学习是机器学习的一个子领域，以解决之前机器学习的限制性问题。由于在各个领域都获得了可观的成效，人工智能在过去的几年中普遍获得了突出的地位。这导致物理学家将注意力集中在了AI这个工具上。他们的目标是更好的理解和丰富他们的直觉。这篇评论文章旨在补充先前提出的方法，以弥合人工智能与物理学之间的鸿沟，并向前迈出了重要的一步，以过滤出由此类漏洞带来的“Babelian” 冲突。这首先需要具备有关通用AI的基础知识。为此，审查的主要重点应放在成为人工神经网络的深度学习模型上。她们是可以通过不同的学习过程进行自我训练的深度学习模型。此外还讨论了马尔可夫决策过程的概念。最后，作为通向主要目标的捷径，本片综述彻底检查了这些神经网络如何能够构建描述某些观察结果的物理理论，而无需应用任何先前的物理知识。
Ⅳ SCINET：物理机器（SCINET: A PHYSICS MACHINE）
现在我们介绍一个机器学习技术在物理学应用的实例，该实例应用神经网络来增强物理学的能力。该方法通常使用实验数据并将其呈现给神经网络，以便提出解释数据的理论。但是，大多数技术都对初始状态空间或数学表达式空间施加了约束。更具体的说，这些技术将我们的物理直觉结合到神经网络中，因此，它们主要是在测试网络的效率和学习性，而不是从头开始输出理论。文献[6]的工作中，通过构造一个名为SciNet的神经网络解决了这个问题，在该网络上没有任何约束或任何先验信息。 SciNet还必须输出完整而充分的描述物理概念公式的参数。这项工作的主要思想如下：
- 向SciNet提供实验数据；
- SciNet发现数据的简单表示；
- 然后SciNet将回答被提出的问题。
SciNet必须能够仅使用其给出的表示来回答问题，而无需返回输入数据。使用两个模型来执行这个步骤：
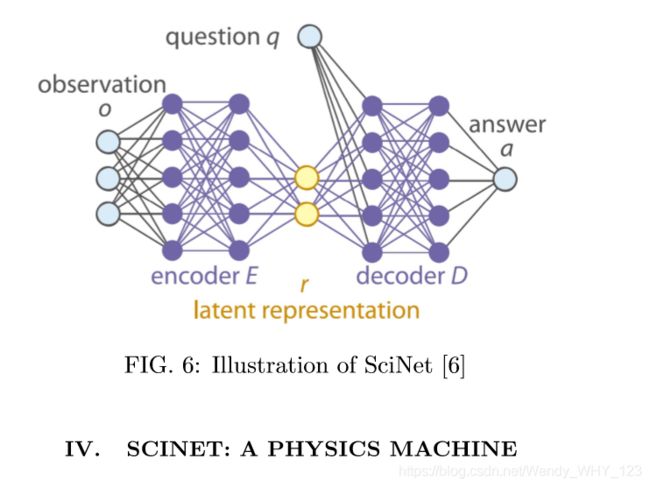
- 编码器：编码器结构由一个或多个神经网络组成。它采用观测值O（实验数据）并将其编码为表示R，表示为机器学习上下文中的潜在表示，因此该映射为：E： O→R。
- 解码器：解码器也是一个神经网络结构。它以编码器产生的潜在表示R和要回答的问题Q作为输入。输出问题的答案，因此映射为： D : R×Q→A。
图6解释了编码器和解码器网络。SciNet的编码器和解码器通过选择的观察数据和问题训练集进行训练，然后使用选择的测试集进行测试以预测准确性。必须注意的是，由于我们以前不知道或不施加潜在神经元的数量（潜在表示的具体数量）。由于潜在神经元的不足，预测的准确性可能降低。从这个意义上讲，在训练阶段，潜伏神经元的数量可以重新设置以适应这些表现。
举一个简单的例子，假设您向SciNet输入了电势U随电流I控制的欧姆定律的函数变化的观察结果。但是SciNet不知道欧姆定律是什么。它只知道输入的观察结果。编码器将找到这些观察结果的表现形式，即代表电阻的参数R并将其储存在潜在的神经元中。通过提供潜在表示和问题（对于给定电流的电势将是多少），解码器可以预测正确的答案（即电流与电势之间的关系）。
接下来介绍文献[6]中提供的一些实例，这些实例演示了SciNet在无任何约束条件和先验知识的情况下，从头预测表示和答案的效率和准确性。
A.实验一：阻尼摆实验（Experiment One: Damped Pendulum）
作为SciNet工作原理的简单经典实例，双摆由以下微分方程描述：
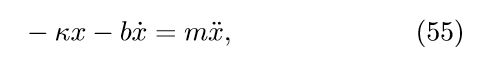
其中κ是控制振荡频率ω的弹簧常数，b是阻尼系数，该阻尼摆系统的解为：
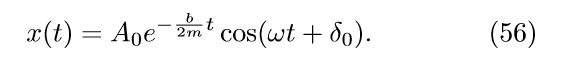SciNet被实现为具有三个潜在神经元的神经网络，并且对钟摆的位置进行了时序观察。对于所有的训练集，固定振幅A0，质量m=1，相位δ0 = 0，仅弹簧常数k和阻尼系数b分别在[5,10]kg/s2 和 [0.5,1]kg/s之间变化。
编码器输出参数k和b，并将其存储在两个潜在神经元中，而无需使用第三个神经元。在提出时间 tpred 作为一个问题时，SciNet 会通过解码器网络以极高的准确性预测当时摆的位置。因此，SciNet能够提取物理参数并进行存储并准确预测未来的位置。 这意味着提取的参数足以描述整个系统并做出未来的预测。
B.实验二：量子位预测（B. Experiment Two: Qubits）
在介绍了一个经典示例之后，SciNet进行了量子示例测试，尤其是量子位测试。 在解释当前问题之前，我们定义了一些使用的术语：
- 量子位：量子位是经典位的量子模拟，是一个二维系统，可以以两个状态的叠加形式存在。 它构成了量子计算的基本单位。
- 量子层析成像：这是一种通过一系列测量重建量子态的方法。一种典型的方法是准备量子态的副本，并对副本进行几次测量。这些测量中的每一个都使我们能够将部分信息存储在状态中。如果该组测量在信息上是完整的，从而允许完全重建量子态，则称它们在层析上是完整的。 否则，它们在断层扫描方面是不完整的。
- 二进制投影测量：产生量子位状态的测量：例如，单个量子位的| 0>或| 1>。
在没有任何先验的量子知识的情况下，给定一组测量值，需要SciNet来表示量子系统的状态并进行准确的预测。在该示例中，我们假设要表示的两个考虑状态是1量子位状态和2量子位状态。单个量子位的实参数量为2，而双量子位的实参数量为6。 以下是我们得到这些数字的方法：
- 对于n个量子位，复数向量空间的维数为2^n，因此对于单个量子位，我们有两种状态：| 0>和| 1>; 对于双量子位，我们有四个状态：| 00>，| 01>，| 10>和| 11>。
- 计算实际参数的个数，我们将得到2×2^n。
- 存在两个约束。 第一个是归一化条件<ψ|ψ>= 1，第二个是全局相位因子不包含任何信息，这意味着拥有ψ’=eiφψ不会影响内积。 这些约束将使参数数量减少两个。
因此，我们应该期望编码器对1量子位使用两个潜在参数，对2量子位使用六个潜在参数。从所有二进制射影测量值M的集合中，选择一个随机子集M1 = {α1，α2，…，αn1}（n1 = 10表示单量子位，30表示2量子位），并将其投影到ψ上，其中ψ 是要表示的量子态。产生的概率p（αi，ψ）是测量量子位为零的概率。重复测量几次后，将产生的概率作为观测值输入网络。根据这些观察结果，SciNet确定足以描述量子态的最小参数数量。
选择另一组随机的二进制投影测量值M2 = {β1，β2，…，βn2}（n2 = 10（单量子位）和30（2量子位）），我们将这些测量值投影到另一个测量值ω上，以生成概率集 p（βi，ω）。这些概率被作为问题反馈给SciNet。 注意，M2被认为是层析上完整的，即ω被完整描述，而M1可能是完整的或不完整的。需要SciNet来预测应用ω测量零的概率p（ω，ψ）= |<ω，ψ>| ²。
对于1量子位系统，并在有足够数量的潜伏神经元（两个神经元）的情况下，鉴于M1在层析成像上是完整的，SciNet可以非常准确地预测概率。当M1在断层扫描上不完整时，错误百分比会很高。 由于准确性不高，因此可以识别断层摄影不完全的集合，并且准确率百分比可以了解集合提供的信息量。
对于2量子位系统，由于有足够数量的神经元（最少6个）和层析成像完整的集合，因此错误的百分比非常低。 对于层析不完全集，无论添加了多少潜伏神经元，错误百分比都很高。因此潜在神经元的个数不影响预测的准确性。
C.实验三：日心说模型（ Experiment Three: Heliocentric Model）
先前的示例是与时间无关的模型。 如此处所述，处理与时间有关的问题需要对SciNet的结构进行一些修改。根据观察结果，编码器输出初始时间r（t0）的表示。 这些表示随时间演变为r（t1），依此类推。 在每个时间步长，解码器网络输出一个答案。
该实验背后的想法是，假定从地球上看火星和太阳的角度，SciNet将在每个时间步长预测这些角度。当我们说从地球上看到的角度时，就好像我们在考虑地心模型（地球位于太阳系的中心）。但是，给定从地球看去的火星θM和太阳θS的角度，SciNet生成潜在表示并存储从太阳看去的地球φE和火星φM的角度。 SciNet构造了日心模型。因此，两个神经元被激活以保存φE和φM。 解码器网络在每个时间步长θi接收这些表示，并根据需要以非常低的错误率（小于0.4％）输出θM（ti）和θS（ti）。
在没有系统的背景知识的情况下，作为神经网络的SciNet成功地以最小数量的物理参数表示物理系统。这是如何从AI和神经网络中获益以达到预期结果的具体示例。
Ⅴ AI物理学家（THE AI PHYSICIST）
首先，值得一提的是关于[6]的工作中实现的机器学习技术的特殊性。内置的神经网络提供了描述特定物理设置的数据集。如第Ⅳ节中详细介绍的，它们的作用是提出描述输入数据的物理理论。麻省理工学院的研究人员也采用了相同的主题，以使用机器学习技术改善我们的物理直觉。但是，他们提出了一个不同问题：是否有可能产出一个可以同时推断描述世界不同方面的理论的AI系统？（即通用AI系统）。为了解决这个问题，Tegmark等人在文献[20]中介绍了一种模仿人类科学家思维方式的ML算法，他们称其为“AI物理学家”。“AI物理学家”代理成功的学习了理论，并将其用于推断未来的领域的特定预测。“AI物理学家”使用四个连续的策略来解决各种复杂的物理问题，其中三个策略是：分而治之、奥卡姆剃刀原则和统一原则。智能代理的另一个关注点是更快学习的能力，即 通过高速学习达到所需的准确性。但是，代理面临的一个主要问题是在接受新任务训练时会忘记已经学习的任务。（即无记忆能力）。忘记先前任务的现象被称为灾难性忘记。“AI物理学家”试图通过第四项也就是最后一项被称为 终生学习 的策略来克服它。这种方法可以通过模拟硬盘存储器中转站理论（Theory Hub）成功实现。
A.框架（ Architecture）
“AI物理学家”按如下方式处理给定数据：
- 理论中心从先前保存的理论空间中提出理论。这些理论描述了部分数据点，并随机初始化了新理论以考虑其余部分。
- 分而治之算法可以训练新的数据并提出新发现的理论，可以最佳地拟合所有数据。首先对它们进行一起训练，以最大程度地降低全局平均损失，然后分别对每个区域进行特定的微调，使其完全适应其描述的区域。
- 然后将定义明确的理论添加到理论中心。
- 奥卡姆（Occam）剃刀算法将经过整理的理论组织起来，将其转化为更简单的符号表达。
- 统一（Unification ）算法将符号理论与主理论结合在一起。
- 然后将主理论和符号理论添加到理论中心，并在遇到新环境时提出建议。
所有的这些步骤可以用图7表示：
在详细解释之前，有必要强调说明一些有助于理解策略的注解。首先，将提供给“AI物理学家”的数据D表征为一个时间序列向量，使得D = {(xt,yt)} = {(xt−T,…,yt−1,yt)} ，理论T定义为一个2元组(f,c)。f时将某个时间步的数据点映射到另一个时间步的数据点的预测函数，而c是将每个数据点分类到其相关域的子分类器。f和c都被具有可学习参数的神经网络实现，因此f的神经网络由两个具有线性激活的隐藏层组成，而子分类器的神经网络具有两个非线性的ReLU激活函数和一个具有线性激活的输出层。
B.学习算法（B. The Learning Algorithm）
1.提出理论（ Proposing theories）
当给“AI物理学家”提供描述以前没有遇到过的新环境数据时，它首先从理论中心提出了描述部分数据的理论。这是证明过去的理论没有被忘记，并在后面重新使用的重要证明。这是终生学习策略的一部分。从描述集合的M个理论总数中，必须从理论中心提出 Mo ≤ M个理论。 Mo 和M之前已经指定。最初，当将数据集D = {(xt,yt)} 提供给主体时，理论中心首先会检查所有已有的理论（步骤一）。对于每个数据点 (xt,yt),代理程序通过最小化相应的损失函数来保存最能描述该数据点的理论的索引i(步骤二)。将所有基于相同理论的数据点添加到前一个数据点，并将所有对应点放到一个记为 D^(i)的数据子集中。在这种情况下，构成了几个子集 D ^(i)，并为每个数据点计算了数据点ni的数量。在所有理论中，然后提出具有最大ni的M0集，因此提出了它们的相应理论。
2.分而治之算法（ Divide-and-conquer algorithm）
引入代理的环境由几种理论描述。如前所述，该理论由其领域子集分类c和函数f组成。该算法的主要思想是：使用子分类器将数据划分为多个域，然后在要征服的域中训练每个函数。函数f的映射xt → yt，并由参数向量θ进行参数化。回想一下，f和c由神经网络实现，并且神经网络的参数是权重和偏差。使用梯度下降来学习和调整参数，以最小化以下损失函数：
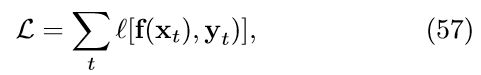
其中l是预测函数f(xt) 产生的输出与实际输出yt之间的差距。
但是，由于所遇到的环境是混合的，其中发现了几种理论，因此每种理论都与其他理论进行竞争，专门研究子集的领域，而全局均值损失为：
这里的损失由参数 γ决定。对于γ的负值，最能降低损失函数l的函数将主导Lγ。换句话说，预测准确性最高的 fi将占主导地位。随着γ越来越小，Lγ趋于等于由拟合函数fi产生的最小损失，即：
由于每个拟合最适合其域，因此全局均值损失得以最小化。有关更多技术细节，请参阅[20]中的附录F。
根据经验发现，γ = −1 适合该过程。它在函数的专用化过程中及在梯度下降过程中给出梯度以改善其理论的过程中效果很好。
寻找最合适其域内数据的函数是将错误最小化的两个过程。首先是使包含所有函数的谐波平均损失L−1最小化。第二个方法是最小化特定函数在其域中的损耗l[fi(xt,yt)] ,作为微调每个函数的一种方式。我们选择l作为描述长度（DL）损失函数：
其中ut = |f(xt) − yt|。描述长度是存储所需的位数，我们的目标是尽可能降低此位数。通过降低损耗l，降低DL。关于子分类c，我们旨在最小化的损失是分类交叉熵损失。这种损失将softmax激活与交叉熵损失结合在一起。softmax激活函数通常用于分类，以使其在所有预测的类之间输出概率最大的类。然后交叉熵检查分类的有效性。这意味着，如果所需类别的概率较低，则将导致较高的交叉熵损失，表明分类不准。
为分而治之的算法开发的算法称为无监督分而治之算法（DDAC）。对于数据集D = {(xt,yt)},M是要训练的初始理论的数量，其中理论中心提出了M0个理论（[20]中的作者使用M = 4和 M0 = 2）。初始精度误差ε0被设置为相当大（使用10），因此损耗
变为二次均方误差（MSE）。在每次迭代之后，将误差设置为中值预测误差。处理方程式（60）中的损失函数非常棘手，这就是为什么将其近似为MSE更好的原因。
该算法通过随机初始化理论中心未提出的M−M0 个理论开始，因此具有M个理论T = {T1,…,TM}，并且函数f通过向量θ: fθ进行参数化。子类c由向量φ: cφ进行参数化，其中θ和φ是可学习的参数。第一阶段是使用谐波损耗 L−1训练理论（步骤2-3）。谐波损耗作为属性传递给子程序迭代训练，后者构成该算法的核心部分。
在子例程的迭代训练步骤中（步骤s1-s10），计算谐波损耗相对于参数θ的梯度，并用于随机梯度下降或Adam 优化算法中，以学习率βf更新该步长（更新的步长，常使用5×10−3 ），对于数组 (xt,yt)，将损失最小化的函数 fi的索引 i保存在参数bt中。
通过这种方式，我们通过最佳函数对每个数据集进行分类。在训练了理论的函数以最大程度减少损失之后，对子分类器进行了训练。在迭代训练的步骤6中，我们需要最小化的损失是交叉熵，为此，我们需要将子分类 cφ 的输出转化为概率输出。这由softmax激活函数完成。将softmax函数应用于cφ(xt)的输出后，它们与 bt一起在交叉熵函数中实现。计算该损失的梯度，并将其用于SGD或 Adam中，以学习率βc (使用10−3 ）更新子分类器的参数φ。使用谐波损失函数 L−1 和交叉熵训练函数和子类别的这些步骤被重复的迭代（作者使用K=10000次的迭代）。
迭代训练中的步骤（s8）检查描述合理数据集的理论（作者使用的阈值时30%），并且如果发现其中一部分（阈值5%）的MSE大于一定数量（使用2×10−6 ），然后初始化另一个理论TM+1并通过迭代训练的步骤 s1- s6 ，计算TM+1的损失。如果此时的损失大于添加新理论之前的损失，则拒绝新理论。否则它将被接受并训练。迭代训练中的步骤（s9)再次检查了理论。如果理论描述了数据集的一小部分（使用0.5%），则将其删除。
对每个函数进行微调的第二阶段遵循与第一阶段相同的步骤，但使用的是损失l。每个阶段也都是迭代完成的，并在每次迭代之后，都会计算精度误差（取误差较低的值）。
3.添加理论（Adding theories）
为了在分治法之后将训练合格的理论添加到理论中心，首先要计算每个理论在其领域中的描述长度dl。只要在此描述长度不超过某个阈值η，就将理论直接添加到理论中心。不仅如此，还添加该理论拟合的数据集，以便了解该理论先前的训练方式。但应用奥卡姆剃刀原理 时，也是有益的，这将在下一部分中解释。
4.奥卡姆剃刀原理（Occam’s razor）
a.概述 Overview
基于有限的数据集进行推理面临着一个重要问题，即模型选择的问题。每当需要在其他竞争性假设中选择一个最能解释给定数据的假设时，就会出现此问题。奥卡姆剃刀原理在解决这一冲突方面起着重要作用。奥卡姆剃刀原理：在相互竞争的假设中，假设数量最少的那个是最适合数据的那个。这意味着所研究的数据通常使用最简单的解释进行模型。
奥卡姆剃刀原理被广泛应用于各个领域，以排除任何不必要的信息和元素。为了使讨论仅限于科学领域，物理学家经常使用Occam的剃刀。以下是两个说明奥卡姆剃刀原理的示例：
- 太阳系的地心说与日心说： 在天文学上，关于太阳系的中心模型存在着古老的争论。为此，有两种相互竞争的理论，第一种被称为地心模型，它指出太阳和行星是围绕着地球转动；另一种被称为日心模型，指出太阳是所有行星的轨道中心。
应用奥卡姆剃刀原理时，没有进行讨论。哥白尼在发现地心模型多年后又发现了日心模型。由于日心模型要简单的多，因此获得了大家的认同。而地心说除了存在一些无法解释的奥秘之外，还包括更复杂的假设。 - 爱因斯坦vs洛伦兹： 在20世纪，出现了尝试解释 时空连续体 的测试。当时的两位物理学家爱因斯坦（Albert Einstein）和亨德里克·洛伦兹（Hendrik Lorentz）解决了这个问题，并用不同的计算方法弥补了所有的数学解释。
洛伦兹的计算是基于这样的解释，即太空中存在一种静止的介质，称为 以太，而爱因斯坦的解释没有以太。由于没有实验证据表明存在这种介质，运用奥卡姆剃刀原理，爱因斯坦的理论更为人们所接受。
b.最小描述长度模式
在学习了所有的理论之后，它们将接受奥卡姆剃刀原理。这种策略（原理）的一种形式包括数学模式，即最小描述长度 (Minimum Description Length Formalism，MDL) 模式。
MDL模式是Rissanen 在1988年提出。给定一个数据集，Rissanen 定义将数据描述为描述长度（DL）的位数。这种模式的两个主要围绕两个想法进行，首先是检测数据中的规律，然后利用它来压缩这些数据。这些规律决定了数据的属性。这样就可以揭示有意义的信息。第二个中心思想指出，只要发现规律性，就会从数据中学习。这意味着，我们压缩数据的次数越多，从中学习的内容就越多。 Rissanen将描述规律性的模型解释为将数据生成为输出的程序。当然，该模型还可以通过其相应的代码来识别。因此，现在将描述长度定义为该程序的比特数，包括压缩数据比特。
c.奥卡姆剃刀算法
在“AI物理学家”的背景下，奥卡姆剃刀算法的主要目标是最小化使用MDL模式，通过DDAC算法获得的预测函数fi的描述长度。域子分类器对每个域都是唯一的，因此考虑最小化其DL 是不切实际的。另一方面，预测功能的重要性在于它可以在其他域中重用或者解决新的传入数据。首先，该算法计算现有理论的描述长度，然后尝试将其最小化。
对于数据集D = {(xt,yt)}，训练的理论为T = {(fi,ci)}。这些理论的DL是每个理论的DL加上其错误的DL：
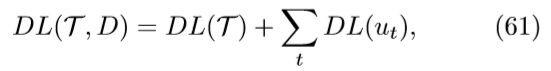
其中ut = |ˆ yt − yt|。（61）式中的第二项已经用 DDAC 算法进行了最小化。奥卡姆剃刀算法只要关注于最小化第一项DL(T)，该项又可以被分解为DL(T) = DL(fθ) + DL(cφ)，其中fθ = (f1,…fM)，cφ = (c1,…cM)。其中DL(fθ)可以被定义为描述f的参数θ的长度：
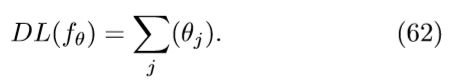
为了最小化DL中的fθ的参数，应用了一些转换，例如collapseLayers, localSnap, integerSnap 等等。这些转换将保持滚动，只要他们使总描述长度 DL(T,D)最小即可。接下来将对这些转换进行详细的解释。
该算法首先将数据集D分解为D(i)（步骤2），每个子集都在其对应的域中。然后，它应用第一个变换collapseLayers（第3步），发现具有线性激活的神经网络的所有连续层并将其合并。如前所述，预测函数可从前一个位置预测当前时间步的位置。localSnap 转换（第4步）会干扰仅考虑更接近要预测的当前时间步长的输入。intergerSnap 转换（第5步）将 fi 中的参数转换为整数，这使总DL最小。例如，给定参数 p = 1.99992,转换后p = 2 ，然后计算新的描述长度。如果此捕捉将DL最小化，则将其占用，否则将其保留。另一个p = 1.6666633示例，算法将尝试转化后为p = 2 并计算DL。如果发现DL增加了，它将离开并尝试另一种转换，即rationalSnap转换，可以近似 p = 1.5 = 3 /2。要计算整数m的描述长度，我们使用：
rationalSnap转换（第6步）用有理数替换fi中的实数或无理参数。这明显减小了 DL(fθ)。例如，如果我们有π = 3.14159265359…，则算法第6步将其转化为p = 355 /113，然后计算DL。可以发现，这种捕捉使总DL最小。要计算以整数m为分子和以自然数n为分母的有理数的描述长度，我们使用：
接下来是toSymbolic （第7步），它将预测函数转化为符号表示。
定义这些转换之后，它们将作为D(i)和ε之外的变量被输入子程序最小化DL函数。子例程将fi，D(i)和转换作为输入，并将转换重复应用于fi。子例程MinimizeDL函数开始计算预测函数的 dl(s2)，然后复制预测函数fclone（s3）并储存它在转换失败的情况下重用。在步骤（s4-s5) 中，算法通过执行变换开始，并考虑了使损失最小化。如果理论i的描述长度dl减少了（采用零步耐心实现），则接受改变换。其中
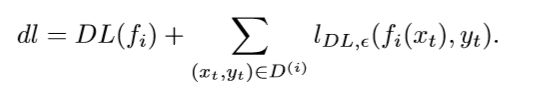
这意味着如果新的描述增加，则直接退出循环，并在转换或fclone（第7步）之前采用预测函数。如果转换保持描述长度不变，重复以上4步重新执行转换；如果dl保持不变，则推出循环。
5.统一算法（Unification algorithm）
为了达到科学的最终目标，即对自然的模拟，该想法不仅是描述观察到的现象，而且还寻求它们之间的联系。这有助于统一这一现象背后的理论。以下算法将显示”AI物理学家“中的积分过程如何发生。
这个算法将采用符号预测函数 {(fi,.)}，并输出主要理论T = {(fp,.)}。通过修改fp中的p，我们可以生成已知预测函数fi的连续体。接下来即将呈现的是关于如何输出或发现一个大师理论。
该算法以符号预测函数作为输入，然后采用这些函数中的每一个并计算其描述长度dl(i)（第1-3步）。在（第4步）中，算法使用（例如）K均值聚类算法（见附录B）基于符号函数的描述长度对符号函数fi进行聚类。因此，预测函数通过簇号k: fik附加标记。统一过程开始于（第5-11步）。首先将预测函数fik转化为二元组(gik,hik)（第6步），其中gik是fik的树枝，而 hik是树干结构。通过应用“子例程规范化”函数执行此转换（步骤s1-s2）。第7、8两步将找到具有相同结构h的树并将它们分组为 Gk。在同一组 Gk中的树的扩散系数由pjk参数化（第9步）。这种参数化将树统一参数化为P的主树。一旦找到主树，该算法会将其重新转化为符号形式（第10步），即主预测函数。最后，该算法将更新 T = {(fpk,.)}中的主函数并返回T。
C.总结获得的知识（Summing up Acquired Knowledge）
为了更好地了解这些算法如何协同工作，必须指定提供给“AI物理学家”的数据。如上所述，数据是向量的时间序列，每个向量都描述了在四个不同领域中徘徊的球的二维运动。每个域的特征都是物理作用，即重力，弹簧，电磁场或弹跳边界。目的是尽可能准确地预测这些粒子的二维运动。“AI物理学家”首先从理论中心提出理论，然后测试它们是否适合部分数据。有了提出的理论和随机初始化的理论之后，代理继续进行分而治之算法。根据文献[20]的结果，“AI物理学家”能够构建用于预测球的未来位置的预测函数，并将它们同时分类为上述四个领域。预先构建的预测函数将传递到奥卡姆剃刀算法中，以最大程度地减小描述长度。在应用这些子例程后，如下执行属于四个领域之一的差分方程之一，即预测函数：
预测函数的描述长度 DL(f) = 212.7。值得一提的是，该方程式是在应用了第一个collapse-Layer转换之后得出的。当应用然后捕捉转换时，它会进一步简化：
具有较小的描述长度DL(f) = 55.6。仍然在奥卡姆剃刀策略中，toSymbolic转换将等式66转化为符号表示：
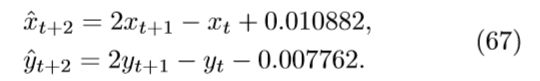
现在剩下的就是找到一种掌握理论的理论，该理论将有关一个主题的预测函数归为一组。为此，“AI物理学家”使用统一算法根据符号预测函数的描述长度对符号预测函数进行聚类，其中聚类的DL在某些阈值之间。最后将等式67归纳为一个主理论fp：
基于这些方程，可以推断出该区域的球受到重力的影响。为了更明确，将等式68重写为：
其中 gi ≡ pi(∆t)²。关于其他三个区域，一个受弹簧影响，一个处于电磁场，一个具有反弹边界。它们的推到方式于该受重力影响的域的推导方式相同。
“AI物理学家”获得的结果非常有前景，因为它优于具有近似相同复杂性的替代神经网络。值得一提的是，终身学习策略在学习算法中的重要性。为了检验这一点，构建了一个新的学习代理，并将其命名为“AI物理学家新生儿”。这个新代理的主要特定是它没有理论中心。这意味着它 没有保存任何先前学习的理论。这是“AI物理学家新生儿”与“AI物理学家”之间的主要区别。两者都达到了完美的精度水平，但是“AI物理学家”的学习速度比其他人快。这意味着 使用以前学习的理论有助于提高学习速度。
1.消除过度领域（1. Eliminating transition domains）
在成功的描述了控制每个领域的理论之后，“AI物理学家”面临着另一个问题，即边界和过度区域。当轨迹从一个不同的物理域移到另一个域时，哪个理论控制运动？AI代理通常从最后一个T = 3个xt = (yt−3,yt−2,yt−1)找到下一个位置。当轨迹接近边界时，先前位置的集合可以包含来自第一个域的3个位置，而不包含来自第二个域的任何位置，包含来自第一个域的2个位置和来自第二个域的1个位置，反之亦然。这四种情况中的每一种都需要一个不同的函数来计算下一个位置。随着添加更多的域，这些情况的数量也会增加。
此外，将域设置为完全弹性的。也就是说，如果轨迹遇到一个域的边界，它将被反弹回来。这些情况还需要不同的函数来管理它们。对于过度和反弹，数据不充分，因此，代理将无法找到解决方案。但是，解决此问题的直接方法是使用以下步骤简单的消除这些区域：
- 对于找到预测未来位置的函数f的每个域 (xt → yt) ，我们找到了预测过去位置的函数(xt → yt−T−1)。
- 当轨迹接近过度区域并使用第一域的未来预测函数时，将执行时间上的外推。外推是轨迹的前向扩展，好像它仍在第一个域中一样。为此正向外推拟合函数yf(t) 。
- 对于相同的轨迹，并使用第二个域的过去预测函数，将执行时间倒推。这种推断是轨迹的向后扩展，就好像它在第二个域中一样。为此，反向外推拟合函数为 yb(t)。
- 我们找到了时间t∗，使得这些函数之间的差异最小。
理想情况下，它将恰好是这两个函数的交点。
如果此刻我们有 yf(t∗) ≈ yb(t∗), 则它是一个边界点。另外，如果y0 f(t∗) ≈ y0 b(t∗)，那么我们要处理的是一个区域与另一个区域之间的过度边界，因为该边界附近的速度在过度时不会不同。否则，边界将是外部边界（反弹）。找到这些点后，将再次训练领域分类器，消除这些点，并尽可能扩展领域。
Ⅵ 结论（ CONCLUSION）
A.结束语（Concluding Remarks）
希望这篇综述有助于在两个科学领域的交叉点上提供对主题的明显见解：人工智能和物理学。在这方面，两个领域在取得重大进展方面共同发挥了重要作用。这篇综述首先介绍了 神经网络，以了解它们在算法中的使用方式以及如何使用不同类型的学习范式对他们进行有效的训练。特别是这些学习范式之一的 强化学习，它是关于在随机环境中对代理的绩效进行建模的关注。整合强化学习技术的问题引起了广泛关注，因为它们体现了以随机行为为特征的现实世界情况。这些问题由所谓的马尔可夫决策过程所描述。神经网络引起的关注是它们在算法中的使用，以帮助提高对观测数据背后的物理理论的理解。其中之一是 SciNet，这是Renato 等人在文献[6]中构建的神经网络模型。它的主要作用是推断观测数据的最小表示形式，以总结其物理环境的所有重要方面。Tegmark 等人在文献[20]中创建的另一种技术“AI物理学家”体现了物理学家的思考和遇到问题的解决方式。该技术分为四种策略，概述了物理学家解决问题的方式。这些提到的技术显示出令人鼓舞的结果。朝着这个研究方向努力的物理学家可以依靠这些结果，并在扩展当前工作方面取得一些进展。未来的研究工作仍然存在许多问题，下一部分将提到其中的一些问题。
B.展望（ Outlook）
人工智能技术对解决物理问题和进一步揭示其背后的直觉做出了巨大贡献。但是，也可以嵌入物理理论来增强AI。重整化组可以在神经网络中作为从数据中提取特征的方案进行说明。超越经典领域，量子相干和量子纠缠在量子计算机中被使用，使其比经典计算机更高效。这些技术可以在机器学习中实现，从而加快了数据处理的速度，但是 量子机器学习仍然遭受着高成本和复杂性的困扰。但是，诸如“对称”和“量规固定”之类的工具可能会最大程度的发挥“AI物理学家”程序的功能。并使我们降低复杂性和降低预期噪声影响的方式，约束其余问题。这些相关问题目前正在研究中。
在这篇综述文章中研究的常规“AI物理学家”显然已经利用了经典计算机。最近，已经提出了一些将机器学习扩展到量子领域中的尝试。出乎意料的是，基于 K核 方法的机器学习（例如矢量机器（SVM）），与量子计算共享一些相似的理论基础，因为它有效的将计算应用于任何大的希尔伯特空间中。这种联系为专家设计量子机器学习方法铺平了道路。为此，在[33]中介绍了一种建立量子神经网络的通用方法。因此，实际工作的自然扩展是将“AI物理学家”升级为量子设置，将我们带入量子AI物理学家的时代。最近获得了巨大发展的一个相关研究是 利用量子启发的张量网络的机器学习。张量网络可以在自适应和无监督学习中使用，类似于归一化重组（RG）。关于此结果的诱人之处是开发的框架，该框架的优点是可以将设计的算法和理论发展统一起来，从而对经典计算和量子计算均具有优势。在这样的统一方案中，应该由“AI物理学家”训练模型，然后将其传递给量子AI物理学家进行进一步优化。进一步研究这种联系并将其应用于凝聚态和高能物理中的问题（例如，AdS/CFT对偶性）将是有益的。
此外，在“AI物理学家”的奥卡姆剃刀中使用SciNet编程以提取最小表示量，可能是进一步减少计算训练时间的一步。这将需要对“AI物理学家”架构进行修改，从而可能会提高性能。
附录
A.激活函数（Activation Functions）
下表列出了常用的激活功能。 它包括每个属性的定义。
B.K-均值聚类（ K-means Clustering）
K-均值聚类的目标很简单：将相似的数据点组合在一起并发现潜在的模式。 该算法在数据集中寻找固定数目的簇数K。 聚类是使用具有一定阈值的距离度量将数据点分组在一起的集合，并且聚簇的数量根据人的选择进行初始化。 这个想法如下：假设有一个庞大的数据集，将这些集合一起训练是非常繁琐且昂贵的。 K-均值聚类算法用于将集合划分为子集，在子集中可以更轻松地自行解决每个聚类。 经过四步总结的迭代之后，该算法收敛到一个解决方案：
- 通过随机选择K个数据点来初始化中心（质心）。
- 通过计算数据点和质心之间的距离，将数据点分配给群集。
- 使用新值更新群集质心，新值是群集中所有数据点的平均值。
- 重复步骤2和3，直到满足以下条件之一：
（a）分配给每个群集的数据点保持不变。
（b）通过重复迭代后，质心固定不变。
（c）数据点和质心之间的最小距离不变。
（d）迭代次数应足以保证收敛。
