or-tools之VRP问题

VRP问题简介：

车辆路线问题（VRP）最早是由Dantzig和Ramser于1959年首次提出，它是指一定数量的客户，各自有不同数量的货物需求，配送中心向客户提供货物，由一个车队负责分送货物，组织适当的行车路线，目标是使得客户的需求得到满足，并能在一定的约束下，达到诸如路程最短、成本最小、耗费时间最少等目的。

由此定义不难看出，旅行商问题（Traveling Saleman Problem,TSP）是VRP的特例，由于Gaery已证明TSP问题是NP难题，因此，VRP也属于NP难题。

车辆路线问题自1959年提出以来，一直是网络优化问题中最基本的问题之一，由于其应用的广泛性和经济上的重大价值，一直受到国内外学者的广泛关注。车辆路线问题可以描述如下（如图1）：

　　

or-tools是目前市面上VRP功能最强的开源算法包，它支持VRP,CVRP,VRP(with multi-depots)等多种复杂情形。

VRP:

or-tools 对VRP的定义如下：

1、只有一个场站（depot）,所有车辆只能从此处出发，到此结束，进行闭环运输；

2、除了场站，其余所有客户（node）必须仅被服务一次；

3、所有车辆的车速都一样；

4、车辆总数不确定；

or-tools中对应的函数为：

RoutingModel routing(size, FLAGS_number_vehicles);//(总客户数,总车数)
routing.SetDepot(depot);//(设定场站)
const Assignment* solution = routing.Solve();//(调用求解引擎)
CVRPSolution cvrp_sol(data, &routing, solution);//(驱动优化结果)

CVRP：

前面VRP问题假设车辆的装载能力无限大，现实生产中，每辆车的装载能力是有限制的，这就引入的CVRP（Capacitated Vehicle Routing Problem）问题，在此情景下，每辆车单条线服务的客户的总需求不能超过车辆的总装载能力。

or-tools中对应的函数为：

std::vector demands(size);//定义一个数组来存储所有客户点的需求
routing.AddVectorDimension(&demands[0], capacity, true, "Demand");//（当前客户点需求，车的装载能力限制，……，……）

同时显示生产中车辆种类繁多，装载能力各不相同，不同种类的车所产生的成本（cost）也不相同，or-tools中同样提供了相应的函数：

void SetVehicleFixedCost(int vehicle, int64 cost);
void AddDimensionWithVehicleCapacity(NodeEvaluator2* evaluator,int64 slack_max,VehicleEvaluator* vehicle_capacity,bool fix_start_cumul_to_zero,const string& name);

 

VRP(with multi-depots)

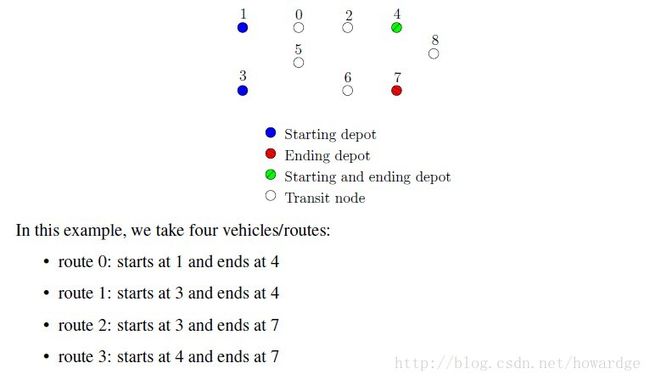
现实生产中同时存在多个场站的情况，那么有些场站只能是出发点，有些只能是结束点，有些既可以是出发点，也可以是结束点如图2。对应这类问题，or-tools提供如下函数：

图2

std::vector > depots(4);
depots[0] = std::make_pair(1,4);
depots[1] = std::make_pair(3,4);
depots[2] = std::make_pair(3,7);
depots[3] = std::make_pair(4,7);
RoutingModel VRP(9, 4, depots);

技巧：

or-tools在进行默认配置下，求解性能可能得不到保障，但是我们可以利用初始解来加速求解，函数如下：

bool RoutesToAssignment(const std::vector >& routes,bool ignore_inactive_nodes,bool close_routes,Assignment* const assignment) const;
const Assignment* solution = routing.Solve(initial_sol);

先到这样里啦！