内部排序（一）插入排序

插入排序分为5种：

直接插入排序、折半插入排序、2-路插入排序、表插入排序、希尔排序。

下面我们来一一介绍：

1、直接插入排序

过程叙述：先将序列中的第1个记录看成是一个有序的子序列，然后从第二个记录起逐个进行插入，直至整个序列变成按关键字非递减有序序列为止。第i趟直接插入排序的操作为：将记录r[i]插入到有序子序列{r[1],r[2]……r[i-1]}中（自i-1起往前搜索，同时后移记录，直至找到插入点，进行插入），变成含有i个记录的有序子序列{r[1],r[2]……r[i-1]}。

注意：
1. 插入成功一个值为一趟。
2. 需要在r[0]处设置监视哨。
3. 整个排序过程进行n-1趟插入。

算法程序：

void InsertSort(SqList &L){
    //对顺序表L做直接插入排序(升序)
    for(i=2;i<=L.length;i++){//控制趟数
        if( L.r[i].key < L.r[i-1].key ){
            L.r[0]=L.r[i];//设置监视哨
            L.r[i]=L.r[i-1];//对r[i-1]进行后移
            for(j=i-2; L.r[0].key < L.r[j].key ;j--){//查找插入点位置。
            //因为第一个if语句已经判断过r[i-1]和r[i](哨兵)的大
            //小，并进行后移操作，故此处从r[i-2]开始。j中最后存放要
            //插入点的下标。

                L.r[j+1]=L.r[j];//不符合条件，后移。
            }
            L.r[j+1]=L.r[0];//进行插入
        }
    }
}

评价：

1.直接插入排序比较次数和移动次数约为(n^2)/4时间复杂度为O（x^2）.
2.适用于n很小的情况。

2、折半插入排序

折半查找原理很简单，就是把直接插入排序过程中的直接查找过程用二分查找代替，即减少比较次数。
算法代码：

void BInsertSort(SqList &L){
//对顺序表L作折半插入排序。
    for(i=2;i<=L.length;i++){//将r[i]插入到r[i~(i-1)]的有序序列中
        L.r[0]=L.r[i];//设置监视哨
        low=1;
        high=i-1;
        while(low<=high){//找出插入点
            m=(low+high)/2;
            if( L.r[0].key < L.r[m].key){
                high=m-1;
            }else{
                low=m+1;
            }
        }

        for(j=i-1;j>=high+1;j--){
            L.r[j+1]=L.r[j];//记录后移
        }

        L.r[high+1]=L.r[0];//插入
    }
}

评价：

1.折半插入排序仅减少了比较次数，而记录的移动次数不便。故时间复杂度依然为O(x^2)。
2.适用于n比较大时。

3、 2-路插入排序

原理：
2-路插入排序是在折半插入排序的基础上再改进，目的是减少排序过程中移动记录的次数。为此需要n个记录的辅助空间。

过程叙述：
另设置一个和L.r同类型的数组d，首先将L.r[1]赋值给d[1],并将d[1]看成是在排好序的序列中处于中间位置的记录，然后从L.r中第二个记录起依次插入到d[1]之前或之后的有序序列中。
通过一个辅助的循环数组, 如果大于最大的元素, 则插入至尾部, 如果小于最小的元素, 则插入至头部,
如果在两者之间, 采用折半查找的方式,移动一部分的元素;
演示

注意：

1. 把d看成一个循环数组。（所谓的循环数组并不是指它们真的首尾相接，而是指逻辑上循环。通过%完成）
   用(x+n)%n取代x，即可完成循环。
2. 设置两个指针first和final分别指示排序过程中得到的有序序列中的第一个记录和最后一个记录在d中的位置。

算法程序：

void TwoRoadInsertSort(int *arr, int *temp, int n)  {
//arr为原数组，temp为临时数组，n为数组长度

    int i, first, final, k;  

    first = final = 0;  
    temp[0] = arr[0];//将arr首元素赋给temp  

    for (i = 1; i < n; i ++) {  
        if (arr[i] < temp[first]) {  // 待插入元素比最小的元素小  
            first = (first - 1 + n) % n;  
            temp[first] = arr[i];  
        } else if (arr[i] > temp[final]) { // 待插入元素比最大元素大  
            final = (final + 1 + n) % n;  
            temp[final] = arr[i];  
        } else { // 插入元素比最小大，比最大小（此过程可自己在上面演示中最后添加元素26，走一遍）note：此处最好用折半查找！！！  
            k = (final + 1 + n) % n;  
            while (temp[((k - 1) + n) % n] > arr[i]) {  
                temp[(k + n) % n] =temp[(k - 1 + n) % n];  
                k = (k - 1 + n) % n;  
            }  
            temp[(k + n) % n] = arr[i];  
            final = (fianl + 1 + n) % n;  
        }  
    }  

    // 将排序记录复制到原来的顺序表里  
    for (k = 0; k < n; k ++) {  
        arr[k] = temp[(first + k) % n];  
    }  
}  

评价：

2-路插入排序首尾插入不需要移动元素。移动次数约为(n^2)/8，可以减少移动次数，并不能避免移动。

4、表插入排序

引入背景：
在2-路插入排序的基础上再减少移动次数，直至不需要移动。用修改指针代替移动！
过程描述：
将静态链表中数组下标为1的分量（结点）和表头构成一个循环链表，然后依次将下标为2至n的分量（结点）按记录关键字非递减有序插入到循环链表中。
过程演示：

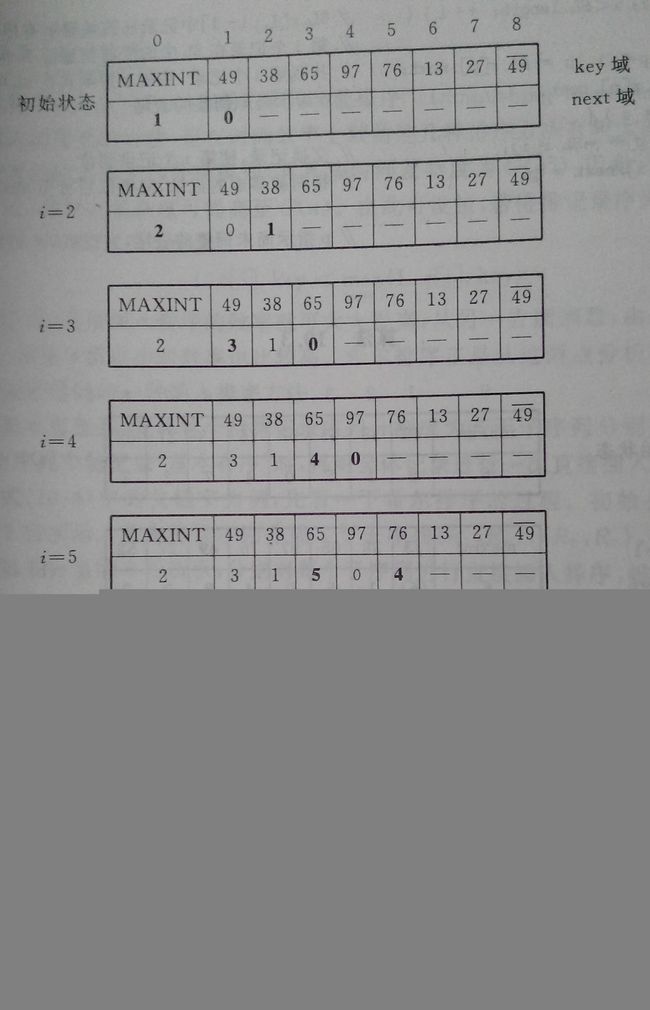
算法代码：

void LinkListInsert(SLinkListType &SL,RedType D[],int n){
  //由数组D建立的n个元素的表插入排序的静态链表SL

  int i,p,q;//q指向当前结点的前一个结点，p指向当前结点
  SL.r[0].rc.key=INT_MAX;//表头结点记录的关键字取得最大整数（非降序表的表尾）
  SL.r[0].next=0;   //next域为0表示表尾（现为空表，初始化）
  for(i=0;i
     SL.r[i+1].rc=D[i];  //将数组D的值赋给静态链表SL
     q=0;
     p=SL.r[0].next;
     while(SL.r[p].rc.key<=SL.r[i+1].rc.key){ 
      //链表从头遍历，直至要插入点结束循环。循环结束时，q指向要插入结点的前一结点，p指向要插入结点。
      q=p;
      p=SL.r[p].next;
     }
     SL.r[i+1].next=p;//修改指针实现插入
     SL.r[q].next=i+1;
  }
  SL.length=n;
}

(重排做法见下面完整代码)
请点击：完整 表插入代码

评价：

表插入排序的基本操作仍是将一个记录插入到已排好序的有序表中，不同之处仅仅是修改2n次指针代替移动记录，排序过程中所需进行的关键字的比较次数相同。时间复杂度仍为O（x^2）.

5、希尔排序

引入背景：
希尔排序是基于插入排序的以下两点性质而提出改进方法的：

1.插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率
2. 但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位

算法描述
希尔排序：将无序数组分割为若干个子序列，子序列不是逐段分割的，而是相隔特定的增量的子序列，对各个子序列进行插入排序；然后再选择一个更小的增量，再将数组分割为多个子序列进行排序……最后选择增量为1，即使用直接插入排序，使最终数组成为有序。
增量的选择：在每趟的排序过程都有一个增量，至少满足一个规则 增量关系 d[1] > d[2] > d[3] >..> d[t] = 1 (t趟排序)；根据增量序列的选取其时间复杂度也会有变化，这个不少论文进行了研究，在此处就不再深究
过程演示：

算法代码：

public static void shellSort(int []array){  
    double increment = array.length;//增量长度  
    int dk,sentinel,k;  
    while (true) {  
        increment = (int)Math.ceil(increment/2);//逐渐减小增量长度  
        dk = (int)increment;//确定增量长度  
        for (int i = 0; i < dk; i++) { //此循环控制趟数 
            //用增量将序列分割，分别进行直接插入排序。随着增量变小为1，最后整体进行直接插入排序  
            for (int j = i+dk; j < array.length; j+=dk) {//此循环控制控制每一趟分组数。  
                k = j - dk;  
                sentinel = array[j];//哨兵位  
                while (k >= 0 && sentinel < array[k]) {//此循环找到插入点。  
                    array[k+dk] = array[k];//k+dk位始终虚位以待  
                    k = k - dk;  
                }  
                array[k+dk] = sentinel;  
            }  
        }  
        //当dk为1的时候，整体进行直接插入排序  
        if (dk == 1) {  
            break;  
        }  
    }  
}