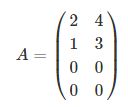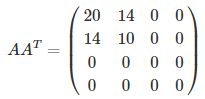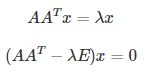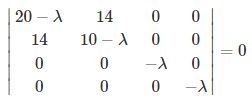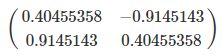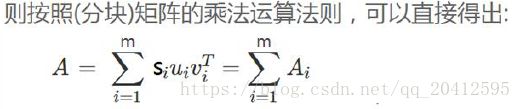机器学习中的数学(4)-线性判别分析（LDA）, 主成分分析(PCA)、奇异值分解（SVD）

1、What & Why PCA（主成分分析）

---

PCA，Principal components analyses，主成分分析。广泛应用于降维，有损数据压缩，特征提取和数据可视化。也被称为Karhunen-Loeve变换

从降维的方法角度来看，有两种PCA的定义方式，方差最大和损失最小两种方式。这里需要有一个直观的理解：什么是变换（线性代数基础）。

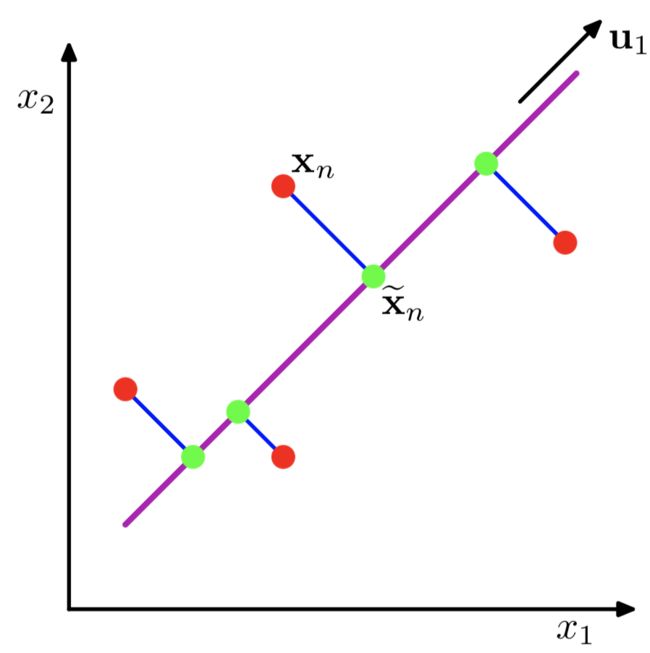
但是总的来说，PCA的核心目的是寻找一个方向（找到这个方向意味着二维中的点可以被压缩到一条直线上，即降维），这个方向可以：

• 最大化正交投影后数据的方差（让数据在经过变换后更加分散）

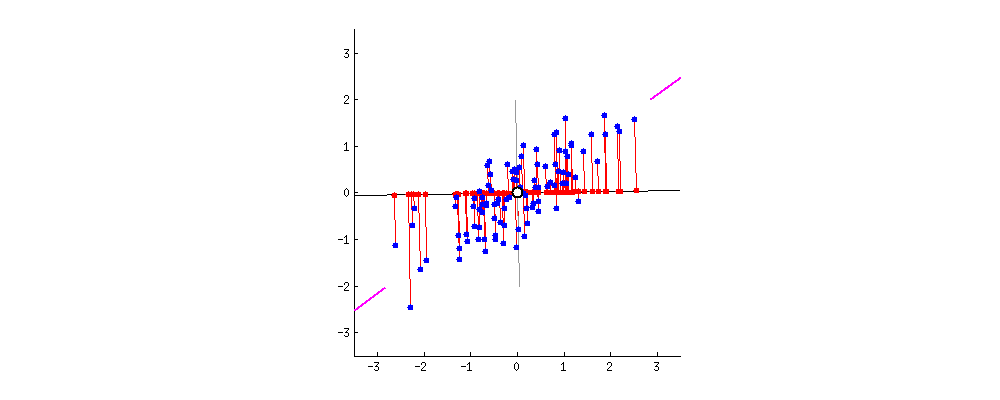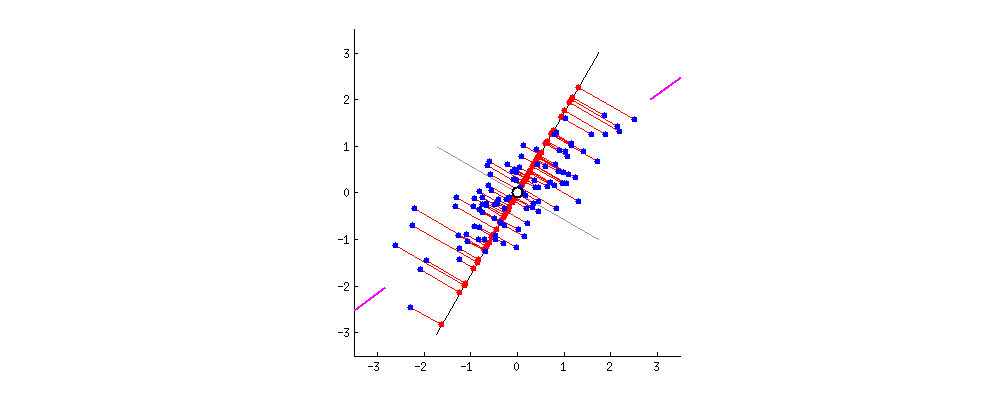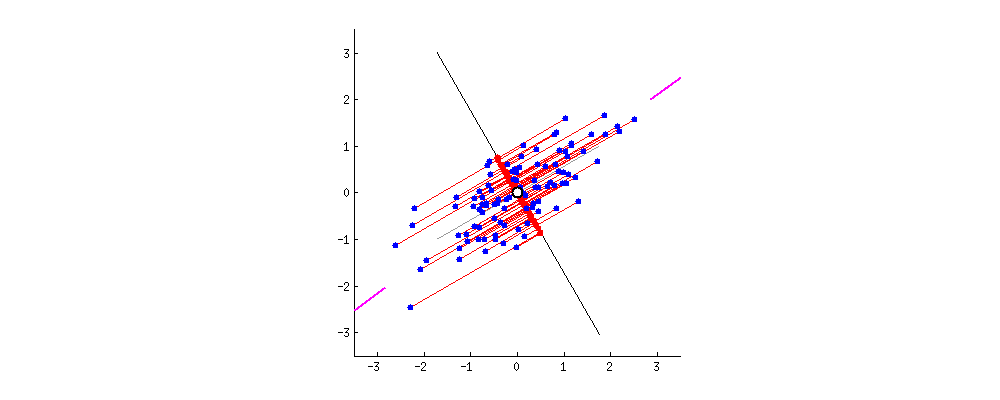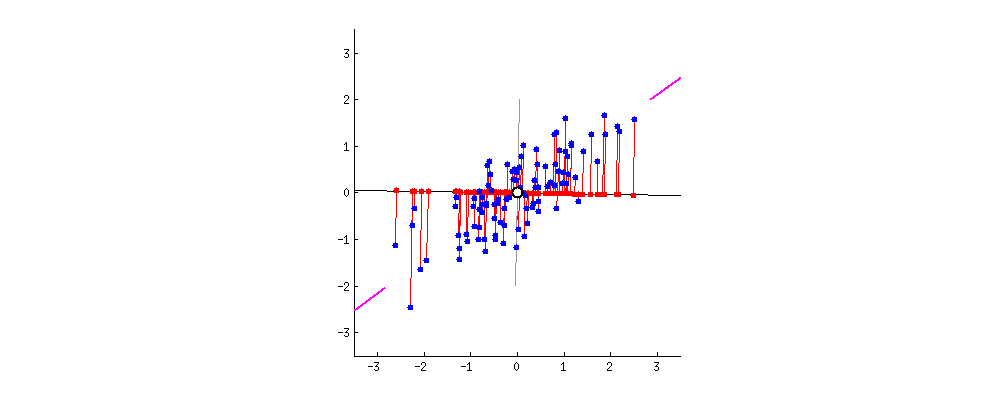
紫色的直线 u1即是关于 x1,x2二维的正交投影的对应一维表示

 

PCA定义为使绿色点集的方差最小（方差是尽量让绿色所有点都聚在一坨）其中的蓝线是原始数据集（红点）到低纬度的距离，这可以引出第二种定义方式

• 最小化投影造成的损失（下图中所有红线（投影造成的损失）加起来最小）

PCA 主成分分析主要目的是为了减少数据维数，其中Auto-encoder也是一种精巧的降维手段。

 

2、奇异值分解（SVD）

---

      详细的描述：机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用 

      SVD不仅是一个数学问题，在工程应用中的很多地方都有它的身影，比如前面讲的PCA，掌握了SVD原理后再去看PCA那是相当简单的，在推荐系统方面，SVD更是名声大噪，将它应用于推荐系统的是Netflix大奖的获得者Koren，可以在Google上找到他写的文章；用SVD可以很容易得到任意矩阵的满秩分解，用满秩分解可以对数据做压缩。可以用SVD来证明对任意M*N的矩阵均存在如下分解：

在开始讲解SVD之前，先补充一点矩阵代数的相关知识。

相关概念

参考自维基百科。

• 正交矩阵：若一个方阵其行与列皆为正交的单位向量，则该矩阵为正交矩阵，且该矩阵的转置和其逆相等。两个向量正交的意思是两个向量的内积为 0
• 正定矩阵：如果对于所有的非零实系数向量 z，都有 ，则称矩阵 A 是正定的。正定矩阵的行列式必然大于 0， 所有特征值也必然 > 0。相对应的，半正定矩阵的行列式必然 ≥ 0。

能学到SVD和PCA的情况下，我这里就默认大家都懂了特征值与特征向量的意义，如果连这2个名词的意义都不懂的话，我建议再回去补一下（我这里不是单纯的指大学里学的如何懂得求特征值、特征向量，这是最lou的了，希望懂的是它的几何意义），这里我就不赘述的去说了。

 它其实对应的线性变换是下面的形式：

上面的矩阵是对称的，所以这个变换是一个对x，y轴的方向一个拉伸变换（每一个对角线上的元素将会对一个维度进行拉伸变换，当值>1时，是拉长，当值<1时时缩短），当矩阵不是对称的时候，假如说矩阵是下面的样子：

在图中，蓝色的箭头是一个最主要的变化方向（变化方向可能有不止一个），如果我们想要描述好一个变换，那我们就描述好这个变换主要的变化方向就好了。反过头来看看之前特征值分解的式子，分解得到的Σ矩阵是一个对角阵，里面的特征值是由大到小排列的，这些特征值所对应的特征向量就是描述这个矩阵变化方向（从主要的变化到次要的变化排列）
       当矩阵是高维的情况下，那么这个矩阵就是高维空间下的一个线性变换，这个线性变化可能没法通过图片来表示，但是可以想象，这个变换也同样有很多的变换方向，我们通过特征值分解得到的前N个特征向量，那么就对应了这个矩阵最主要的N个变化方向。我们利用这前N个变化方向，就可以近似这个矩阵（变换）。也就是之前说的：提取这个矩阵最重要的特征。总结一下，特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征是什么，可以将每一个特征向量理解为一个线性的子空间，我们可以利用这些线性的子空间干很多的事情。不过，特征值分解也有很多的局限，比如说变换的矩阵必须是方阵。

       下面谈谈奇异值分解。特征值分解是一个提取矩阵特征很不错的方法，但是它只是对方阵而言的，在现实的世界中，我们看到的大部分矩阵都不是方阵，比如说有N个学生，每个学生有M科成绩，这样形成的一个N * M的矩阵就不可能是方阵，我们怎样才能描述这样普通的矩阵呢的重要特征呢？奇异值分解可以用来干这个事情，奇异值分解是一个能适用于任意的矩阵的一种分解的方法：

注意：本篇文章内如未作说明矩阵均指实数矩阵。

假设有 m×n 的矩阵 A ，那么 SVD 就是要找到如下式的这么一个分解，将 A分解为 3 个矩阵的乘积：

其中，U和 V都是正交矩阵，而 Σ就是一个非负实对角矩阵。

 

SVD求解

U和 V的列分别叫做 A的 左奇异向量（left-singular vectors）和 右奇异向量（right-singular vectors），Σ 的对角线上的值叫做 A的奇异值（singular values）。

其实整个求解 SVD 的过程就是求解这 3 个矩阵的过程，而求解这 3 个矩阵的过程就是求解特征值和特征向量的过程，问题就在于 求谁的特征值和特征向量。

• U 的列由 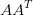 的单位化过的特征向量构成
• V的列由 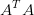 的单位化过的特征向量构成
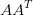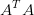• Σ的对角元素来源于  或  的特征值的平方根，并且是按从大到小的顺序排列的

知道了这些，那么求解 SVD 的步骤就显而易见了：

1. 求 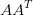的特征值和特征向量，用单位化的特征向量构成 U
2. 求 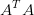的特征值和特征向量，用单位化的特征向量构成 V
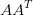3. 将  或者 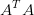的特征值求平方根，然后构成 Σ

举例

那么可以计算得到

接下来就是求这个矩阵的特征值和特征向量了

可以得到 λ1≈29.86606875，λ2≈0.13393125，λ3=λ4=0，有 4 个特征值。

对应的单位化过的特征向量为：

这就是矩阵 U了。

同样的过程求解 ATAATA 的特征值和特征向量，求得 λ1≈0.13393125，λ2≈29.86606875，将特征值降序排列后对应的单位化过的特征向量为：

这就是矩阵 V了。

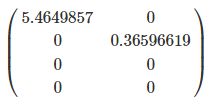
而矩阵 Σ根据上面说的为特征值的平方根构成的对角矩阵

到此，SVD 分解就结束了，原来的矩阵 A就被分解成了 3 个矩阵的乘积。

对奇异值分解的理解

     紧接上面所说，为什么SVD能够抽取数据里的主要特征呢，前面还一直没有谈到，那接下来就着重说说奇异值分解的一些内在含义。

分解之后再截断近似计算：

这里我们借用分块矩阵来叙述：

我们将U按列进行分块，有U=（u1,u2,u3,...un）,V按行向量进行划分，有V=（v1,v2,v3,...vm）

这里我们要注意，中表示的一个列向量，表示的是一个行向量，他们相乘将会得到一个mxn的矩阵(同原矩阵一样的大小，只是值不同而已），在乘上对应的特征值，表示这个乘起来的矩阵的重要程度，那么原矩阵A就被分解成了m个相同大小的分矩阵的和（分矩阵的维度为mxn）。

近似计算的形象理解

利用矩阵分块乘法展开得：

这样矩阵的乘法看起来像是下面的样子：

整个SVD的推导过程就是这样的。

3、奇异值与主成分分析（PCA）

       主成分分析在上面也讲了一些，这里主要谈谈如何用SVD去解PCA的问题。PCA的问题其实是一个基的变换，使得变换后的数据有着最大的方差。方差的大小描述的是一个变量的信息量，我们在讲一个东西的稳定性的时候，往往说要减小方差，如果一个模型的方差很大，那就说明模型不稳定了。但是对于我们用于机器学习的数据（主要是训练数据），方差大才有意义，不然输入的数据都是同一个点，那方差就为0了，这样输入的多个数据就等同于一个数据了。以下面这张图为例子：

        这个假设是一个摄像机采集一个物体运动得到的图片，上面的点表示物体运动的位置，假如我们想要用一条直线去拟合这些点，那我们会选择什么方向的线呢？当然是图上标有signal的那条线。如果我们把这些点单纯的投影到x轴或者y轴上，最后在x轴与y轴上得到的方差是相似的（因为这些点的趋势是在45度左右的方向，所以投影到x轴或者y轴上都是类似的），如果我们使用原来的xy坐标系去看这些点，容易看不出来这些点真正的方向是什么。但是如果我们进行坐标系的变化，横轴变成了signal的方向，纵轴变成了noise的方向，则就很容易发现什么方向的方差大，什么方向的方差小了。

      一般来说，方差大的方向是信号的方向，方差小的方向是噪声的方向，我们在数据挖掘中或者数字信号处理中，往往要提高信号与噪声的比例，也就是信噪比。对上图来说，如果我们只保留signal方向的数据，也可以对原数据进行不错的近似了。

      PCA的全部工作简单点说，就是对原始的空间中顺序地找一组相互正交的坐标轴，第一个轴是使得方差最大的，第二个轴是在与第一个轴正交的平面中使得方差最大的，第三个轴是在与第1、2个轴正交的平面中方差最大的，这样假设在N维空间中，我们可以找到N个这样的坐标轴，我们取前r个去近似这个空间，这样就从一个N维的空间压缩到r维的空间了，但是我们选择的r个坐标轴能够使得空间的压缩使得数据的损失最小。

       还是假设我们矩阵每一行表示一个样本，每一列表示一个feature，用矩阵的语言来表示，将一个m * n的矩阵A的进行坐标轴的变化，P就是一个变换的矩阵从一个N维的空间变换到另一个N维的空间，在空间中就会进行一些类似于旋转、拉伸的变化。

      而将一个m * n的矩阵A变换成一个m * r的矩阵，这样就会使得本来有n个feature的，变成了有r个feature了（r < n)，这r个其实就是对n个feature的一种提炼，我们就把这个称为feature的压缩。用数学语言表示就是：

      但是这个怎么和SVD扯上关系呢？之前谈到，SVD得出的奇异向量也是从奇异值由大到小排列的，按PCA的观点来看，就是方差最大的坐标轴就是第一个奇异向量，方差次大的坐标轴就是第二个奇异向量…我们回忆一下之前得到的SVD式子：

在矩阵的两边同时乘上一个矩阵V，由于V是一个正交的矩阵，所以V转置乘以V得到单位阵I，所以可以化成后面的式子

     将后面的式子与AxP那个mxn的矩阵变换为mxr的矩阵的式子对照看看，在这里，其实V就是P，也就是一个变化的向量。这里是将一个mxn的矩阵压缩到一个mxr的矩阵，也就是对列进行压缩，如果我们想对行进行压缩（在PCA的观点下，对行进行压缩可以理解为，将一些相似的sample合并在一起，或者将一些没有太大价值的sample去掉）怎么办呢？同样我们写出一个通用的行压缩例子：

这样就从一个m行的矩阵压缩到一个r行的矩阵了，对SVD来说也是一样的，我们对SVD分解的式子两边乘以U的转置U'

这样我们就得到了对行进行压缩的式子。可以看出，其实PCA几乎可以说是对SVD的一个包装，如果我们实现了SVD，那也就实现了PCA了，而且更好的地方是，有了SVD，我们就可以得到两个方向的PCA，如果我们对进行特征值的分解，只能得到一个方向的PCA。

4、线性判别分析（LDA）

---

详细的讲解移到：PCA&LDA的详细推导

 

参考资料：

https://charlesliuyx.github.io/2017/10/05/%E3%80%90%E7%9B%B4%E8%A7%82%E8%AF%A6%E8%A7%A3%E3%80%91%E4%BB%80%E4%B9%88%E6%98%AFPCA%E3%80%81SVD/

https://blog.csdn.net/u010099080/article/details/68060274

https://blog.csdn.net/zhongkejingwang/article/details/43053513

https://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html