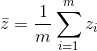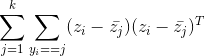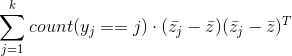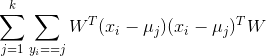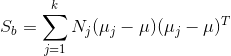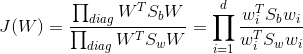机器学习 线性判别分析（linear discriminant analysis）

一、基本原理

1. 模型形式

LDA模型主要用于分类数据的降维，往往每个样本会有很多属性以及一个所属类别，假设有d个属性，那么样本空间就是d维的，通过LDA模型可以将d维数据投影到某个超平面，从而降低维度。这个超平面也不是随便选择的，它需要同一类的样本投影到超平面后距离尽量小，同时，不同类的样本投影到超平面后距离又要尽量大。说白了就是映射到超平面后，相当于聚了个类，同一类的尽量待在一块，不同类尽量隔开。

假设数据集，对于每个样本有n个属性，那么降维后的样本如下所示

                                                                                 ​​​​​​​​​​​​​​​​​​​​​

其中，，

2. 模型求解

该模型主要考虑的就是让降维后的数据的类内距尽可能小，类间距尽可能大。样本整体均值为

                                                                             

第j类样本的均值为

                                                                  

那么类内距可以用类内方差来表示

                                                                  

类间距可以用类间方差来表示

                                                          

假设原数据各类均值为，整体均值为，又因为，类内方差可以转换成

                                                            

令为第j类样本的个数，则类间方差转换为

                                                              

定义类内散度矩阵

                                                           

定义类间散度矩阵

                                                              

那么优化函数可以定义为

                                                                                

当该优化函数最大时，W为最优解，由于都是矩阵，不易求解，故采用矩阵的迹来代替上述表达式

                                                   

其中为W第i列，这样这个优化函数就变成一个数了。接下来要求的最大值。根据广义瑞利商的相关结论（这里不作详述了），的最大值为矩阵的最大的d个特征值的乘积，W为这些对应特征向量组成的矩阵。（之间要线性无关的，所以不能都取最大特征值）

二、代码实现

#author jiangshan
#date 2018-7-18
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt

# data prepare
iris = datasets.load_iris()

X = iris.data
X = X.T
y = iris.target
target_names = iris.target_names
class_num = target_names.shape[0]
dim_num = X.shape[0]
dim_goal = 2
aver_class = np.zeros((dim_num,class_num))
Sw = np.zeros((dim_num,dim_num))
Sb = np.zeros((dim_num,dim_num))
w = np.zeros((dim_num,dim_goal))

# main process
aver_all = np.average(X,axis=1)
for i in range(class_num):
    aver_class[:,i] = np.average(X[:,y==i],axis=1)

for i in range(class_num):
    d1 = X[:,y==i]-aver_class[:,i:i+1]
    Sw_i = np.dot(d1,d1.T)
    Sw = Sw + Sw_i
    d2 = aver_class[:,i]-aver_all
    d2 = d2.reshape((dim_num,1))
    Sb = Sb + len(np.where(y==i))*np.dot(d2,d2.T)

S = np.dot(np.linalg.inv(Sw),Sb)
e,v = np.linalg.eig(S)
e_sorted = -np.sort(-e)

for i in range(dim_goal):
    id = np.where(e==e_sorted[i])[0][0]
    w[:,i] = v[:,id][:]

# transformed data
z=np.dot(w.T,X)
z=z.T

plt.figure()
for c,i,target_name in zip("rgb",[0,1,2],target_names):
    plt.scatter(z[y==i,0],z[y==i,1],c=c,label=target_name)
plt.legend()
plt.title('LDA of IRIS dataset')
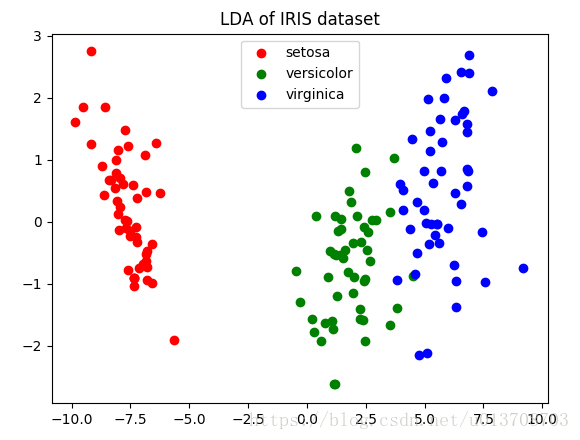
plt.show()

效果图：

原本数据是四维的，每个样本含有4个属性，现在降维到2维空间了，可以看出在2维空间，数据间分割还是比较明显的。

三、调用sklearn库

import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

iris = datasets.load_iris()

X = iris.data
y = iris.target
target_names = iris.target_names

lda = LinearDiscriminantAnalysis(n_components=2)
X_r = lda.fit(X,y).transform(X)

plt.figure()
for c,i,target_name in zip("rgb",[0,1,2],target_names):
    plt.scatter(X_r[y==i,0],X_r[y==i,1],c=c,label=target_name)
plt.legend()
plt.title('LDA of IRIS dataset')
plt.show()