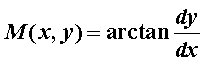图像边缘检测——二阶微分算子（下）Canny算子（Matlab实现）

1986年，John Canny提出了一种边缘检测的方法，即Canny算子，是目前使用最多的边缘检测算法。

John Canny研究了最优边缘检测方法所需的特性，给出了评价边缘检测性能优劣的三个指标：

1  好的信噪比，即将非边缘点判定为边缘点的概率要低，将边缘点判为非边缘点的概率要低；

2 高的定位性能，即检测出的边缘点要尽可能在实际边缘的中心；

3 对单一边缘仅有唯一响应，即单个边缘产生多个响应的概率要低，并且虚假响应边缘应该得到最大抑制。

他将边缘检测看成一个标准的信号处理问题，寻找最优滤波器。

Canny算子解决了前面提到的二阶微分丢失边缘方向信息的问题，同时保持了二阶微分检测边缘的精确和方便。

Canny算子

步骤如下：

1.用高斯低通滤波器平滑图像；

2.计算低通图像的梯度幅值和方向；

3.薄化，对图像进行非极大值抑制；

4.用“双阈值”检测和连接边缘。

1.高斯平滑如前所述，没什么特殊之处。

2.计算梯度强度场和角度场

其中，

梯度强度为：

梯度方向为：

3.非极大值抑制（non-maximal suppression）

或者称薄化（thinning），目的是细化直接使用梯度幅值图像带来的宽边缘。具体做法是保留边缘法向过零点（边缘法向就是梯度的方向），即保留满足

的点。或者说保留梯度方向的上的极大值点。

其中

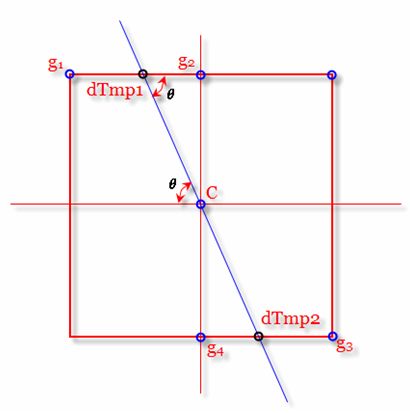
对于像素点C，要确定C是不是局部最大值点，蓝线代表C的梯度方向。由梯度定义可知，这个局部最大值点就在这个方向上。所以只要把C点梯度值和dTemp1、dTemp2的梯度值比较即可，（亚像素点dTemp1、dTemp2的梯度值可以通过插值得到）。如果C的梯度大于这两个点的梯度值，则C是局部最大值点，保留；如果C的梯度小于二者任意一个，则C不是局部最大值点，令其梯度为0，即M（xc,yc）=0。

当然这个步骤可以简化。在工程上，方向可以做离散化处理，Canny将方向划分为四个角度：0，pi/4，pi/2，3pi/4。将中心像素的梯度方向归到离它最接近的那个角度上。

4.双阈值检测

这一步可以减少假边缘的数量。首先得到梯度幅值的直方图，一种方案是选取占直方图70%的梯度幅值为高阈值，占直方图50%的梯度幅值为低阈值。

这样可以得到两幅边缘图像（strong edge， weak edge），使用高阈值得到的图像，含有很少的假边缘，但是因为阈值较高，产生的边缘可能不闭合。双阈值法要在高阈值图像中把边缘点连接成闭合的轮廓，当到达轮廓的端点时，算法就在该端点的8领域点中寻找可以连接到轮廓上的低阈值点作为边缘，这样，算法不断地在低阈值图像中收集边缘，直到高阈值图像的边缘闭合为止。

创新点：

Canny算子只关注边缘法向有大的变化的点，我们知道，不同图像在同一点的边缘方向是不一样的，所以这是一个依赖数据的图像处理算法，我们称之为图像内容相关或者图像内容驱动。

Canny算子在Matlab上的演示效果：

代码：

lenna = imread('E:\ImageTest\512\g512_006\lena.pgm');
subplot(221)
imshow(lenna,[]);title('原图')

%  BW = EDGE(I,'canny') specifies the Canny method.
%
%   BW = EDGE(I,'canny',THRESH) specifies sensitivity thresholds for the
%   Canny method. THRESH is a two-element vector in which the first element
%   is the low threshold, and the second element is the high threshold. If
%   you specify a scalar for THRESH, this value is used for the high
%   threshold and 0.4*THRESH is used for the low threshold. If you do not
%   specify THRESH, or if THRESH is empty ([]), EDGE chooses low and high
%   values automatically.
%
%   BW = EDGE(I,'canny',THRESH,SIGMA) specifies the Canny method, using
%   SIGMA as the standard deviation of the Gaussian filter. The default
%   SIGMA is sqrt(2); the size of the filter is chosen automatically, based
%   on SIGMA.

lenna_1 = edge(lenna,'canny',0.09); 
subplot(222)
imshow(lenna_1,[]);title('Canny 0.09')

lenna_2 = edge(lenna,'canny',0.15); 
subplot(223)
imshow(lenna_2,[]);title('Canny 0.15')

lenna_3 = edge(lenna,'canny',0.2); 
subplot(224)
imshow(lenna_3,[]);title('Canny 0.2')