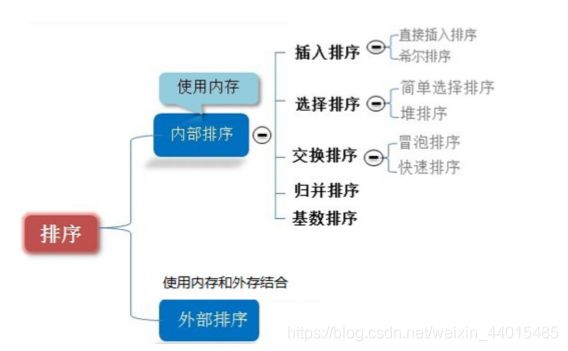
八大排序算法代码详解以及时间复杂的比较
八大排序算法代码详解以及时间复杂的比较
这马上都大三了,虽然老师上课也在讲,但自己也没咋听,现在排序算法就会个冒泡,真的太差劲了,趁暑假补起来!这玩意真的很重要!
好了现在开始讲代码了
一.冒泡排序
原理:
从前往后依次将当前值与下一个值进行比较,若发现逆序则交换,每次循环后吐出最大(小) 值,所以叫冒泡
代码`
public static void maopao(int arr[]){
int temp=0;
boolean bol=false;
for(int i=0;i<arr.length-1;i++){
for(int j=0;j<arr.length-1-i;j++){
if(arr[j]>arr[j+1]){
bol=true;
temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
if(!bol){
break;
}else{
bol=false;
}
}
}
此处对冒泡排序进行了优化,定义布尔变量,若发现一次循环中没有发现交换,说明数组已经有序,直接跳出循环,降低时间复杂度。
二.选择排序
原理:
第一次从arr[0]~arr[n-1]选出最小值与arr[0]交换,第二次从arr[1]-arr[n-1]中选出最小值与arr[1]交换,第三次从arr[2]-arr[n-1]中选出最小值与arr[2]进行交换…进行n-1次交换,得到一个从小到大得序列。
**这看似与冒泡和相似,实际大大降低了时间复杂度,冒泡是没遇到一个逆序得数据就交换一次,而选择排序只需要交换n-1次,降低了时间复杂度。**我的电脑测试八万个数据,冒泡大概需要七八秒,而选择只需要一两秒就能搞定。
代码:
public static void SelectSort(int []arr){
for(int i=0;i<arr.length;i++){
int minIndex=i; //定义比较值得索引
int min=arr[i]; //中间变量min
for(int j=i+1;j<arr.length;j++){
if(min>arr[j]){ //发现arr[j]更小,保存其索引和值
minIndex=j;
min=arr[j];
}
}
//若minIndex得值未改变,不需进行交换
//若minIndex得值改变,交换两个变量
if(minIndex!=i){
arr[minIndex]=arr[i];
arr[i]=min;
}
}
}
三.插入排序
原理:
**把n个待排序得元素看成一个有序表和一个无序表,开始时有序表只有一个元素arr[0],无序表中有n-1个元素,排序过程中每次从无序表中取出第一个元素,把他依次与有序表中得元素进行比较,插入到合适得位置。使之成为新的有序表。
排序思路图:

代码:
//插入排序
public static void insertSort(int []arr){
for(int i=1;i<arr.length;i++){
//从第一个开始插入,依次取出后面得元素进行插入
int insert=arr[i];
//待插入得前一个数据得索引
int insertIndex=i-1;
while(insertIndex>=0&&insert<arr[insertIndex]){
//若待插入数据小于前一个数据,将当前索引得数据赋值为前一个数据得值
//每次循环中,都交换一次数据,完成数组后移
arr[insertIndex+1]=arr[insertIndex];
//索引提前完成下一次比较
insertIndex--;
}
//跳出循环,插入数据
arr[insertIndex+1]=insert;
}
}
**
四.希尔排序
原理:
对于插入排序来说,如果最小的数位于数组最后,需要进行n-1次后移,大大降低了算法效率。希尔排序可以说是插入排序的改进版,将数组按一定增量的等间隔gap(一开始gap=arr.length/2)分组,对组类的数进行插入排序,每排序一次后,gap=gap/2,再次进行插入排序,此时数组已经一步步接近有序,直到gap==1;间隔为1的数组即为原数组,再插入时,插入的次数已经非常少,数组有序。
思想:
减少插入的次数,降低时间复杂度
原理图
//希尔排序
public static void shellSort(int []arr){
//将数组分成以gap为间隔得多个数组进行比较,直到gap==0,每次gap/2,是间隔变小
for(int gap=arr.length/2;gap>0;gap/=2){
//从索引gap开始,对多个数组进行插入排序
//以下和插入排序类似
for(int i=gap;i<arr.length;i++){
int j=i;
int temp=arr[j];
if(arr[j]<arr[j-gap]){
while(j-gap>=0&&temp<arr[j-gap]){
arr[j]=arr[j-gap];
j-=gap;
}
arr[j]=temp;
}
}
}
}
**
五.快速排序
**
原理:
在原数组上指定一个基准数,将比基准数小的移到其左边,比基准数大的移到其右边,在对两边的数再次进行此操作,也就是递归的思想,直到数组有序。
具体操作请看代码,以最左边的数为基准数为例。代码有每步详解。
代码:
//快速排序
//left为数组的开始索引,right为数组的结束索引
public static void quickSort(int []arr,int left,int right){
int i,j,temp,t;
//此时待移动的数组只有一个数,默认有序,直接跳出方法
if(left>right){
return;
}
i=left;
j=right;
//以最arr[0]最左边的数为基准
temp=arr[left];
//i不断++,j不断--,跳出循环时,i==j
while(i<j){
//从右往左,找到比基准数大的数,记录此时的下标j
while(temp<=arr[j]&&i<j){
j--;
}
//从左往右,找到比基准数小的数,记录其下边i
while(temp>=arr[i]&&i<j){
i++;
}
//交换两个数的位置
if(i<j){
t=arr[j];
arr[j]=arr[i];
arr[i]=t;
}
}
//此时i==j
//因为是以arr[left]为基准,此时arr[i]一定小于arr[left]
//交换arr[i]与arr[left]的位置,使得arr[i]左边的数
arr[left]=arr[i];
arr[i]=temp;
//向左递归
quickSort(arr,left,j-1);
//向右递归
quickSort(arr,j+1,right);
}
**
六.归并排序
**
原理:
采用分而治之的的方法,将数组分成若干部分-------分,再将各个部分排序在一起-------治。见图:

在治的过程中,初始化一个中间数组temp,每次将要合并的两个数组从头开始比较,小的先填充到temp中,分后的若干个数组不断的合并,采用递归的思想,最终合并成一个有序的序列,若数组的长度为n,则需合并n-1次。见下图:
 这是最后一次合并的思维图,更小的序列合并亦是如此。
这是最后一次合并的思维图,更小的序列合并亦是如此。
代码:
代码中有各个步骤的详细解答,请看注释
public class MergetSort {
public static void main(String[] args) {
int[] arr={34,2,1,54,32,65,3,23,12,342,213,756,3,2,0,-98,-54,345,534,5,-1};
int[] temp=new int[arr.length];
mergetSort(arr,0,arr.length-1,temp);
System.out.println(Arrays.toString(arr));
}
//分+合的方法
public static void mergetSort(int []arr,int left,int right,int []temp){
if(left<right){
int mid=(left+right)/2; //中间索引
//向左递归分解
mergetSort(arr,left,mid,temp);
//向右递归分解
mergetSort(arr,mid+1,right,temp);
//合并
merget(arr,left,mid,right,temp);
}
}
//合并的方法
/**
*
* @param arr 需要归并的数组
* @param left 左边序列的初始索引
* @param mid 中间索引
* @param right 右边索引
* @param temp 做中转的数组
* 合并的方法一共由三步实现
* 1.先把两边的有序的数据按照顺序填充到temp数组中
* 2.将有剩余的一边的数据全部填充到temp中
* 3.将temp拷贝到arr
*/
public static void merget(int[] arr,int left,int mid,int right,int[] temp){
int i=left; //初始化i,左边序列的初始索引
int j=mid+1; //初始化j,右边序列的初始索引
int t=0; //指向temp数组的当前索引
//步骤(一)
while(i<=mid&&j<=right){
if(arr[i]<=arr[j]){ //如果左边的数组小于走遍的数,将其填充到temp中
temp[t]=arr[i];
t++;
i++;
}else{ //否则将右边的数填充到temp中
temp[t]=arr[j];
t++;
j++;
}
}
//步骤(二)
while(i<=mid){
temp[t]=arr[i];
i++;
t++;
}
while(j<=right){
temp[t]=arr[j];
j++;
t++;
}
//步骤(三)
t=0;
int lefttemp=left;
while(lefttemp<=right){
arr[lefttemp]=temp[t];
t++;
lefttemp++;
}
}
}
这里需要大家用心专研了,博客看十遍,不如理解记忆后自己写一边!
七.基数排序(桶排序)
原理:
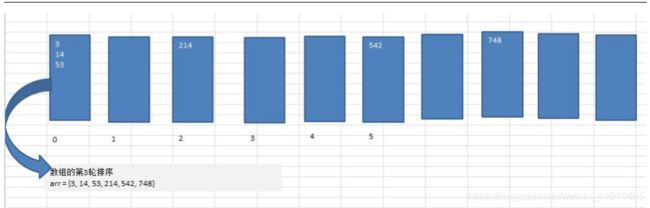
1,将所有数看作相同的位数长度,不够的前面补零,从最低位开始,依次进行比较。
2,定义十个桶,按顺序0,1,2…分别放入当前位数为该下标的数值。
3,循环最高位的个数的次数,每次循环清空十个桶,得到一个有序序列
4,图文说明:(更清晰易懂)

 代码:
代码:
代码有每一步详解
public static void radixSort(int []arr){
//1.得到数组中最大的数的位数
int max=arr[0];
//找到最大的数
for(int i=1;i<arr.length;i++){
if(arr[i]>max)
max=arr[i];
}
int maxLength=(max+"").length();//得到最大位数
//定义一个二维数组,表示10个桶,每个通就是一个一维数组
//1.二维数组包含10个一维数组
//2.为了防止溢出,每个一维数组的大小为arr.length
//3.典型的空间换时间算法
int[][] bucket=new int[10][arr.length];
//为了记录每个桶实际放了多少数据,定义一个一维数组来记录每次放入的数
//比如:bucketElementCounts[0],记录的是bucket[0]桶放入的数据个数
int[] bucketElementCounts=new int[10];
//开始循环处理
for(int i=0,n=1;i<maxLength;i++,n*=10){
//针对每个数组的对应位数进行排序,第一次是个位,第三次是十位。。。。。
for(int j=0;j<arr.length;j++){
//取出每个元素对应位的值
int digiOfElement=arr[j]/n%10;
//放入对应的桶中
bucket[digiOfElement][bucketElementCounts[digiOfElement]]=arr[j];
bucketElementCounts[digiOfElement]++;
//上面两行代码需要理解一下,digiOfElement表示位数
//bucketElementCounts[digiOfElement]表示位数为digiOfElement存放了几个值,所以每次需++;
}
//按照桶的顺序,取出原数组
int index=0;
//遍历每个桶
for(int k=0;k<10;k++){
if(bucketElementCounts[k]!=0){
for(int l=0;l<bucketElementCounts[k];l++){
arr[index++]=bucket[k][l];
}
}
//!!!!!!切记,一定要把bucketElementCounts[k]清零
bucketElementCounts[k]=0;
}
}
}
以上都是我通过学习尚硅谷韩老师算法课学习的,讲课非常清晰易懂,有的内容也是参照了韩老师的课堂资料,如有侵权请联系我。
韩老师课程链接
希望这篇博客对你我都有所帮助